原価値入率設定 売価と値入額

原価値入率設定 売価と値入額

原価値入率設定 売価と値入額_v1.1

• ダウンロード元は当サイトと同じサーバ内です。
• 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
• ダウンロードしたファイルは自由に改変して頂いて構いません。
• 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
• 内容に関するご質問などは、こちらからお願いします。

Excel ダウンロード

Excelテンプレート

• 売価と値入額から原価値入率を求める。

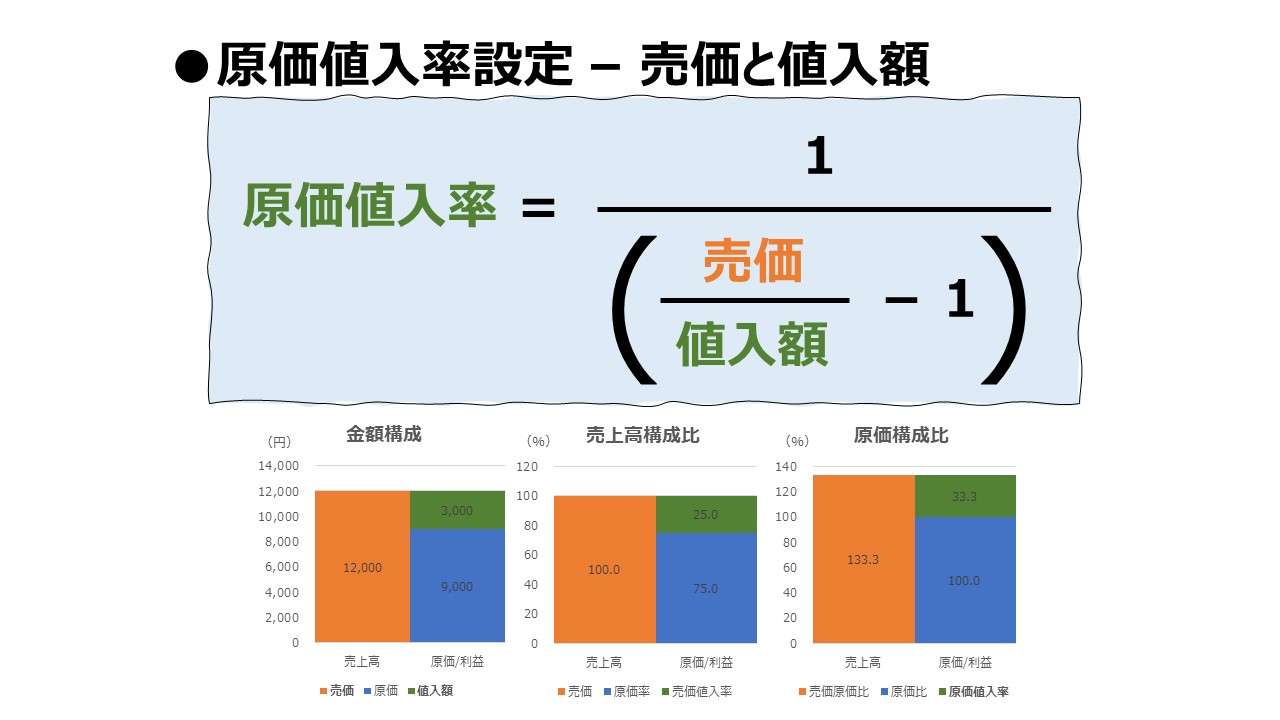
計算式

例）
\( \displaystyle \bf 原価値入率=\frac{1}{\frac{100}{20}-1} = \frac{1}{5-1} = 25.0\% \)

式展開）
商の恒等式から

\( \displaystyle \bf 原価値入率=\frac{値入額}{原価} \)

利益恒等式：売価 = 原価 + 値入額 より式を変形して 原価 = 売価 － 値入額 これを上式に代入すると

\( \displaystyle \bf 原価値入率=\frac{値入額}{売価-値入額} = \require{cancel} \frac{\frac{\cancel{値入額}}{\cancel{値入額}}}{\frac{売価-値入額}{値入額}} = \frac{1}{\frac{売価}{値入額}-\frac{\cancel{値入額}}{\cancel{値入額}}} = \frac{1}{\frac{売価}{値入額}-1}\)

説明

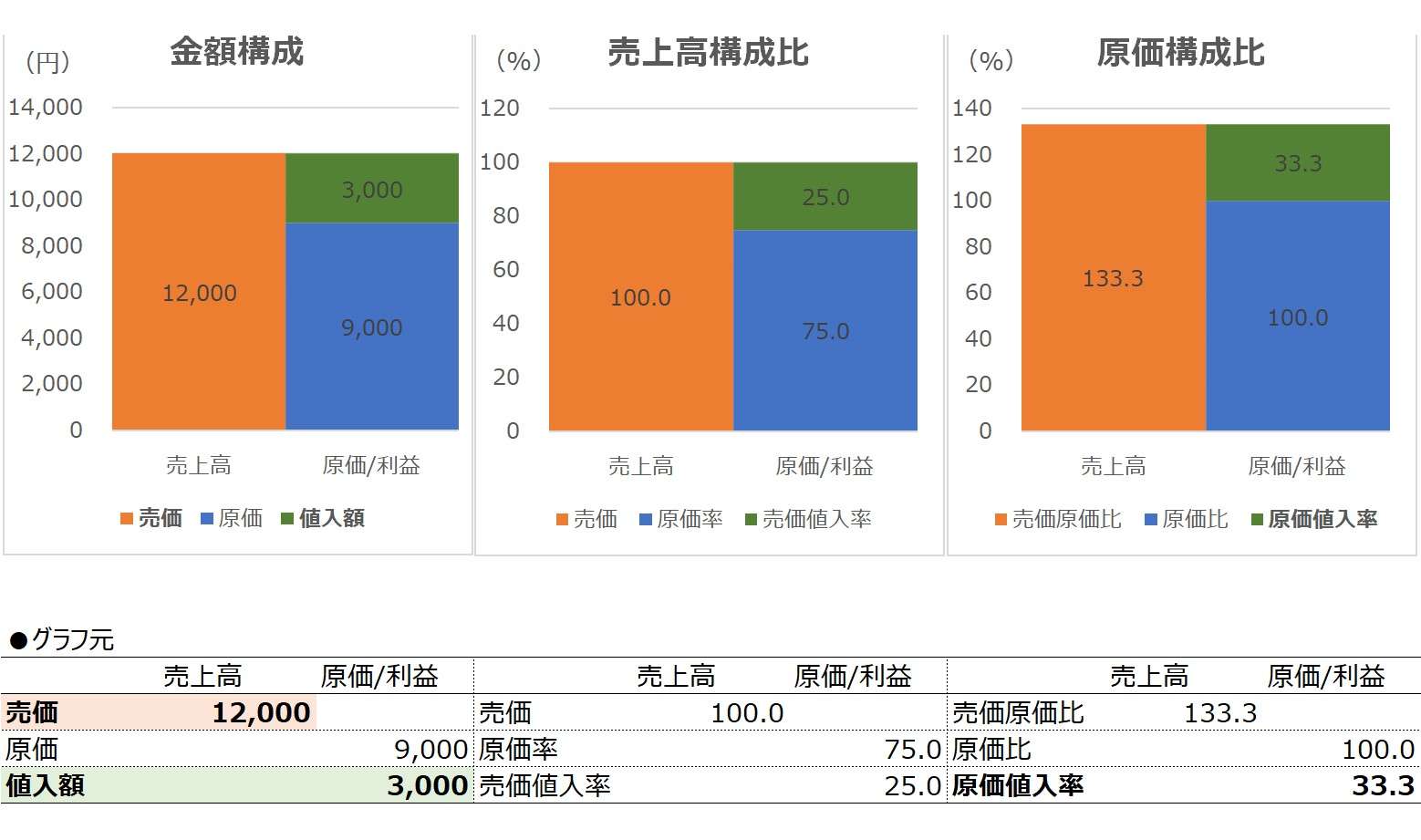
入力欄の青字になっている「売価」「値入額」に任意の数字を入力すると、表とグラフを自由に操作することができる。

なお、利益恒等式：売価 ＝ 原価 + 値入額 より、売価と値入額が分かっているときは、自ずと原価も定まる。

よって、売価と値入額から間接的に把握できた原価と、最初から判明している値入額により

\( \displaystyle \bf 原価値入率 = \frac{値入額}{原価} \)

という商の恒等式を導ける。

あえて、原価の値を用いずに原価値入率を売価と値入額だけで表すと本稿の公式となる。

どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。

自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。

「値入率」と「粗利益率」ってどう違うの？

値入率と粗利益率の違いを知らない人は意外と多いようです。今回は、その違いを解説します。

md-next.jp

原価企画とは？必要性や進め方をわかりやすく解説！

原価企画とは製品製造の初期段階での原価管理活動です。具体的にどんな活動なのか、自社でも行う必要があるのか、判断しかねていませんか。この記事では、原価企画の概要から必要性やメリット、進め方、効率化方法までわかりやすく解説します。適切な原価管理...

it-trend.jp

値入率・原価・値入額・売価・原価率の求め方 | 販売士クラブ

値入率や原価の計算方法などを具体的な例で求め方を説明。

hanbaisikaku.com

原価値入率

#	計算式	Excelテンプレート
㉜	\( \displaystyle \bf 原価値入率=\frac{値入額}{原価} \)	原価値入率設定 原価と値入額
33	\( \displaystyle \bf 原価値入率=\frac{売価}{原価}-1 \)	原価値入率設定 売価と原価
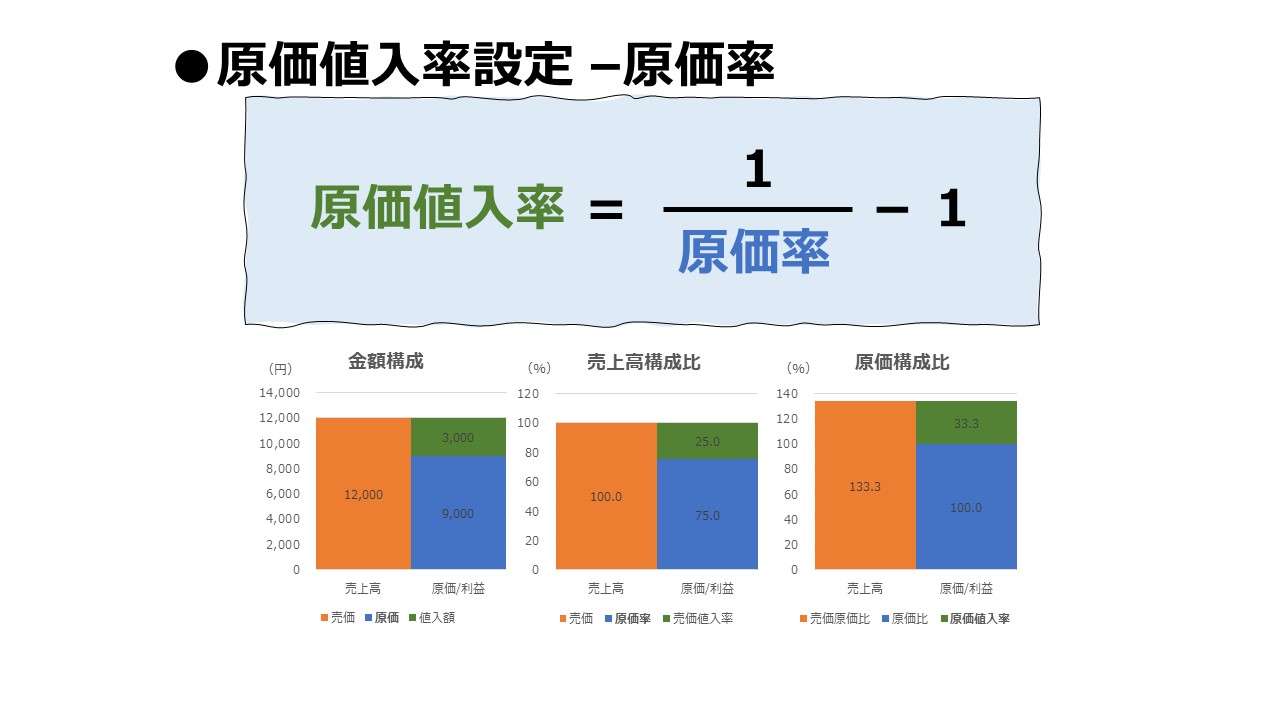
34	\( \displaystyle \bf 原価値入率=\frac{1}{原価率}-1 \)	原価値入率設定 原価率
35	\( \displaystyle \bf 原価値入率=\frac{1}{\frac{売価}{値入額}-1} \)	原価値入率設定 売価と値入額
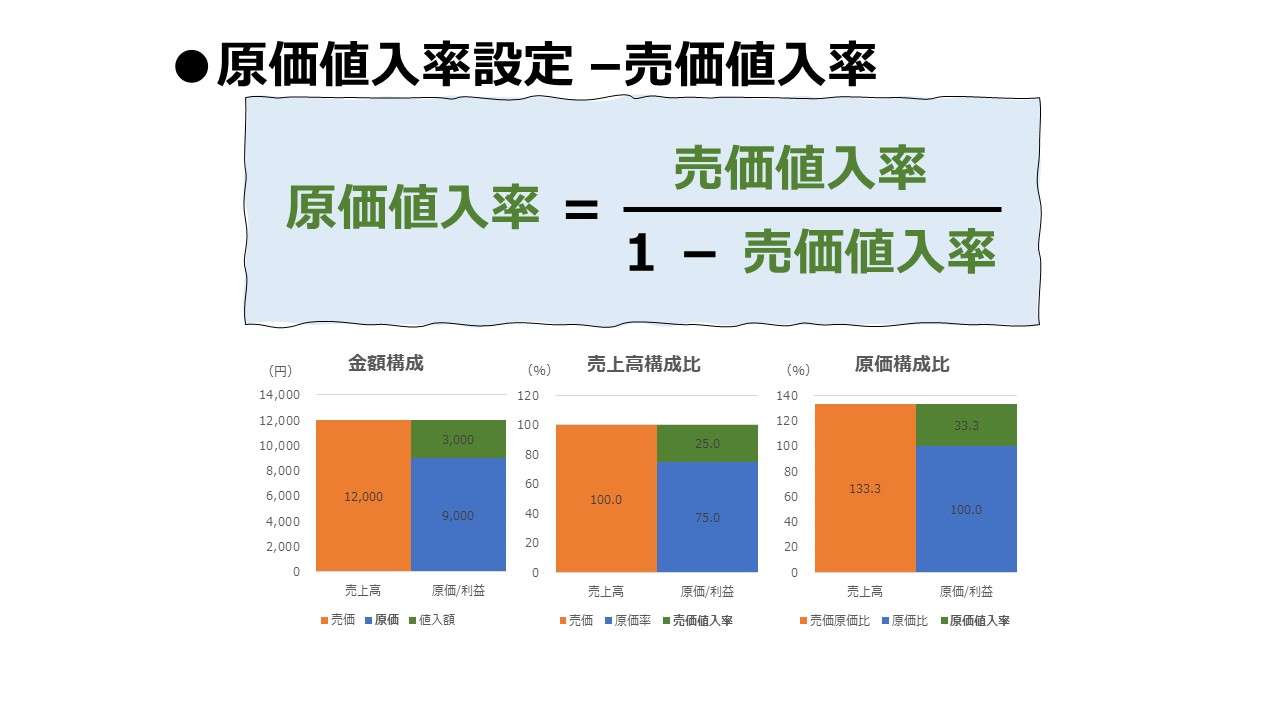
36	\( \displaystyle \bf 原価値入率=\frac{売価値入率}{1-売価値入率~~~~~} \)	原価値入率設定 売価値入率

公式一覧