テンプレート
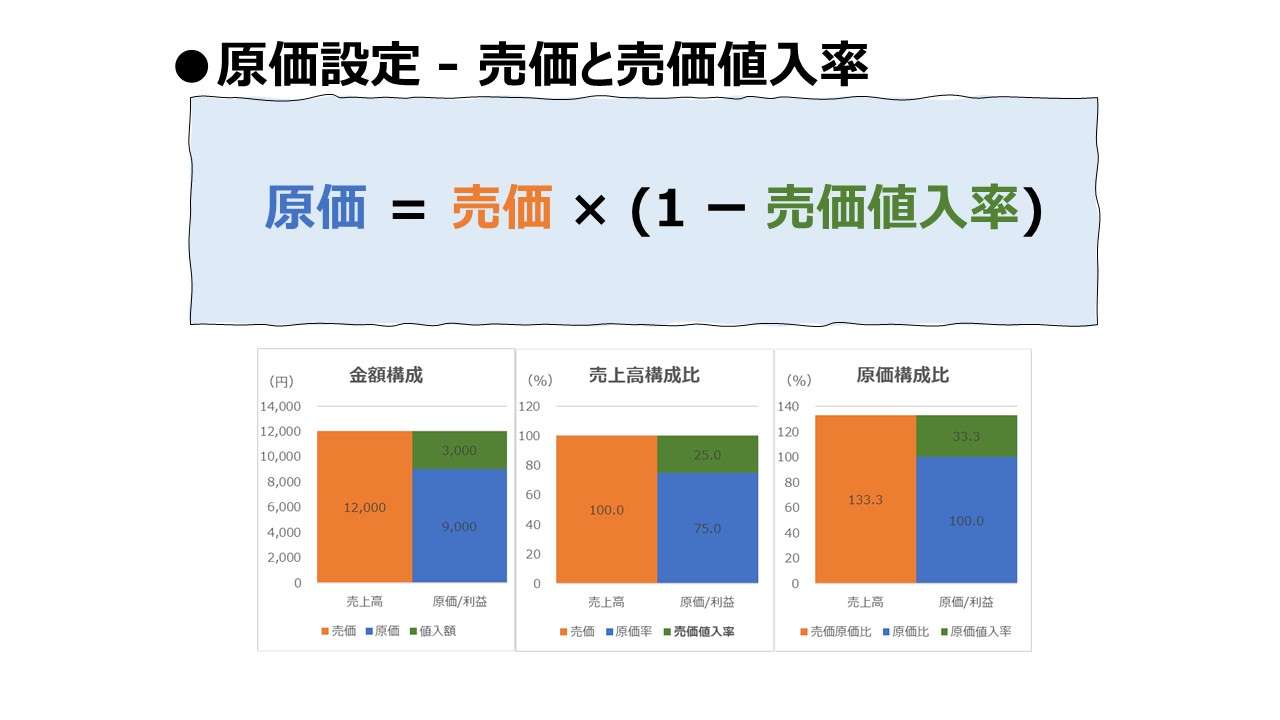
- 売価(販売価格)と売価値入率から原価を求める。
計算式
\( \displaystyle \bf 原価=売価\times(1-売価値入率) \)
例)
\( \displaystyle \bf 原価=100 × (1 – 20\%) = 80 \)
式展開)
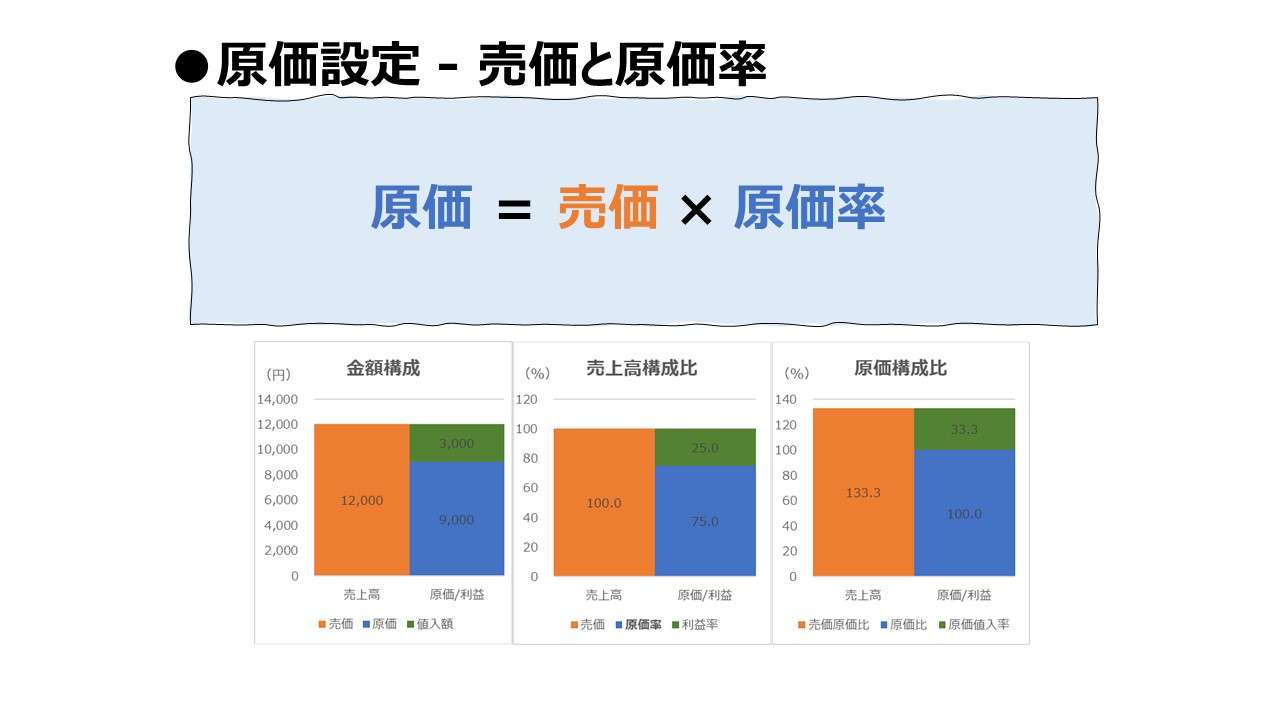
\( \displaystyle \bf 原価 = 売価 \times 原価率 \)
\( \displaystyle \bf 原価 = 売価 \times \frac{原価}{売価} \)
\( \displaystyle \bf 原価 = 売価 \times \frac{売価 – 値入額}{売価} \)
\( \displaystyle \bf 原価 = 売価 \times \left(\frac{売価}{売価} – \frac{値入額}{売価} \right) \)
\( \displaystyle \bf 原価 = 売価 \times (1 – 売価値入率) \)
説明
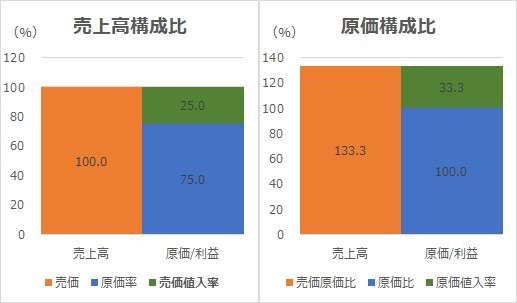
入力欄の青字になっている「売価(販売価格)」「売価値入率」に任意の数字を入力すると、表とグラフを自由に操作することができる。
この式は、所定の売価の想定の下で、希望利益率(=売価値入率)を確保するために、目指すべき原価の額を求めようとする場合の基本式である。
このような原価の求め方は、原価企画/ターゲットコストの考え方が背景にある。
類似の公式に、
\( \displaystyle \bf 原価=売価-値入額 \)
がある。
両者の違いは、利益(≒値入額)を求めるのに、”絶対額”か、それとも”率”を前提条件にするかの差でに過ぎない。TPOに応じて使い分ける。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新(F5押下など)すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
特になし


原価設定
| # | 計算式 | Excelテンプレート |
|---|---|---|
| ❽ | \( \displaystyle \bf 原価=売価-値入額 \) | |
| ⑨ | \( \displaystyle \bf 原価=売価\times原価率 \) | |
| 10 | \( \displaystyle \bf 原価=売価\times(1-売価値入率) \) | |
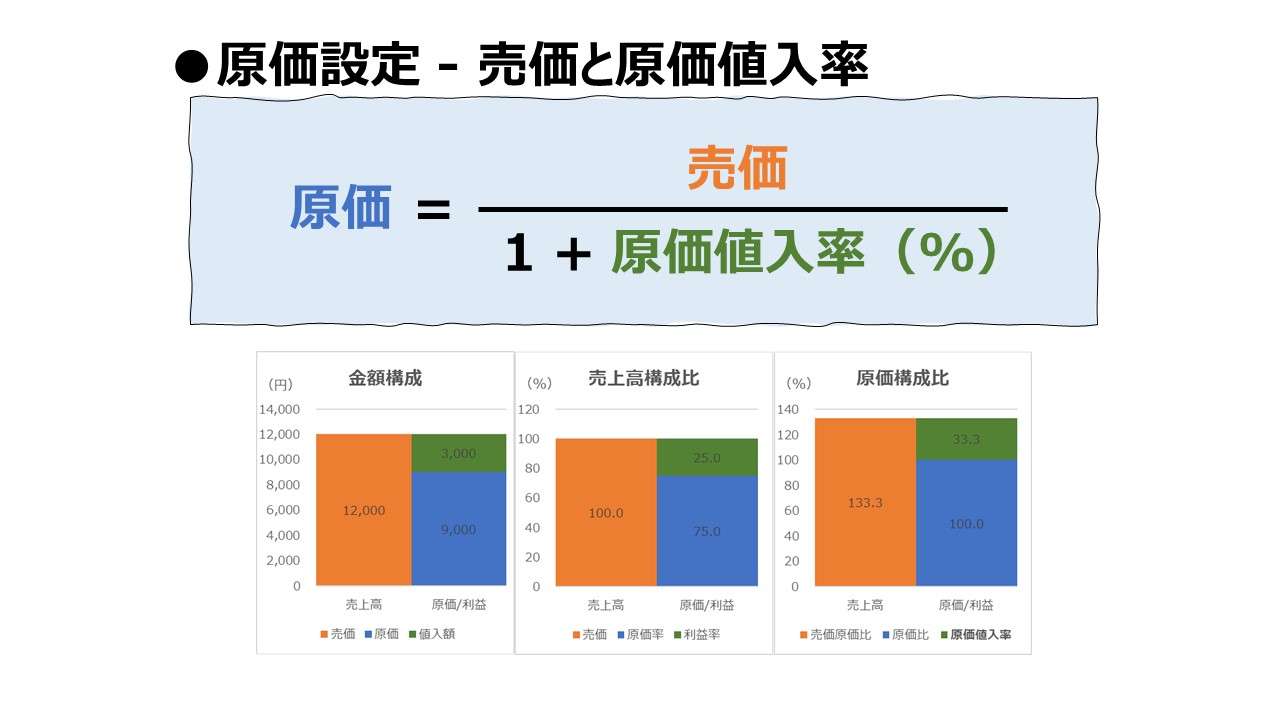
| 11 | \( \displaystyle \bf 原価=\frac{~~~~~~~~~~~~売価~~~~~~~~~~~~~~~}{(1+原価値入率)~~~~~}\) | |
| ⑫ | \( \displaystyle \bf 原価=\frac{値入額}{原価値入率}\) | |
| 13 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{1-原価率~~~~~}-1\right)\) | |
| 14 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{売価値入率}-1\right)\) |
公式一覧
| # | 計算式 | 売価 | 原価 | 値入額 | 原価率 | 売価値入率 | 原価値入率 |
|---|---|---|---|---|---|---|---|
| ❶ | \( \displaystyle \bf 売価=原価+値入額 \) | ● | ○ | ○ | |||
| ② | \( \displaystyle \bf 売価=\frac{原価}{原価率}\) | ● | ○ | ○ | |||
| 3 | \( \displaystyle \bf 売価=\frac{~~~~~~~~~~原価~~~~~~~~~~~~~~~}{1-売価値入率~~~~~}\) | ● | ○ | ○ | |||
| 4 | \( \displaystyle \bf 売価=原価\times(1+原価値入率) \) | ● | ○ | ○ | |||
| ⑤ | \( \displaystyle \bf 売価=\frac{値入額}{売価値入率}\) | ● | ○ | ○ | |||
| 6 | \( \displaystyle \bf 売価=\frac{~~~~~~~~値入額~~~~~~~~~~~}{1-原価率~}\) | ● | ○ | ○ | |||
| 7 | \( \displaystyle \bf 売価=値入額\times\left(\frac{1}{原価値入率}+1\right)\) | ● | ○ | ○ | |||
| ❽ | \( \displaystyle \bf 原価=売価-値入額 \) | ○ | ● | ○ | |||
| ⑨ | \( \displaystyle \bf 原価=売価\times原価率 \) | ○ | ● | ○ | |||
| 10 | \( \displaystyle \bf 原価=売価\times(1-売価値入率) \) | ○ | ● | ○ | |||
| 11 | \( \displaystyle \bf 原価=\frac{~~~~~~~~~~~~売価~~~~~~~~~~~~~~~}{(1+原価値入率)~~~~~}\) | ○ | ● | ○ | |||
| ⑫ | \( \displaystyle \bf 原価=\frac{値入額}{原価値入率}\) | ● | ○ | ○ | |||
| 13 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{1-原価率~~~~~}-1\right)\) | ● | ○ | ○ | |||
| 14 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{売価値入率}-1\right)\) | ● | ○ | ○ | |||
| ⓯ | \( \displaystyle \bf 値入額=売価-原価 \) | ○ | ○ | ● | |||
| ⑯ | \( \displaystyle \bf 値入額=売価\times売価値入率 \) | ○ | ● | ○ | |||
| 17 | \( \displaystyle \bf 値入額=売価\times(1-原価率) \) | ○ | ● | ○ | |||
| 18 | \( \displaystyle \bf 値入額=\frac{売価}{\frac{1}{原価値入率}+1} \) | ○ | ● | ○ | |||
| ⑲ | \( \displaystyle \bf 値入額=原価\times原価値入率 \) | ○ | ● | ○ | |||
| 20 | \( \displaystyle \bf 値入額=原価\times\left(\frac{1}{原価率}-1\right) \) | ○ | ● | ○ | |||
| 21 | \( \displaystyle \bf 値入額=\frac{原価}{\frac{1}{売価値入率}-1} \) | ○ | ● | ○ | |||
| ㉒ | \( \displaystyle \bf 原価率=\frac{原価}{売価} \) | ○ | ○ | ● | |||
| 23 | \( \displaystyle \bf 原価率=1-\frac{値入額}{売価} \) | ○ | ○ | ● | |||
| 24 | \( \displaystyle \bf 原価率=1-売価値入率 \) | ● | ○ | ||||
| 25 | \( \displaystyle \bf 原価率=\frac{1}{1+\frac{値入額}{原価}}\) | ○ | ○ | ● | |||
| 26 | \( \displaystyle \bf 原価率=\frac{1}{1+原価値入率~~~~~}\) | ● | ○ | ||||
| ㉗ | \( \displaystyle \bf 売価値入率=\frac{値入額}{売価}\) | ○ | ○ | ● | |||
| 28 | \( \displaystyle \bf 売価値入率=1-\frac{原価}{売価}\) | ○ | ○ | ● | |||
| 29 | \( \displaystyle \bf 売価値入率=1-原価率\) | ○ | ● | ||||
| 30 | \( \displaystyle \bf 売価値入率=\frac{1}{\frac{原価}{値入額}+1} \) | ○ | ○ | ● | |||
| 31 | \( \displaystyle \bf 売価値入率=\frac{原価値入率}{1+原価値入率~~~~~} \) | ● | ○ | ||||
| ㉜ | \( \displaystyle \bf 原価値入率=\frac{値入額}{原価} \) | ○ | ○ | ● | |||
| 33 | \( \displaystyle \bf 原価値入率=\frac{売価}{原価}-1 \) | ○ | ○ | ● | |||
| 34 | \( \displaystyle \bf 原価値入率=\frac{1}{原価率}-1 \) | ○ | ● | ||||
| 35 | \( \displaystyle \bf 原価値入率=\frac{1}{\frac{売価}{値入額}-1} \) | ○ | ○ | ● | |||
| 36 | \( \displaystyle \bf 原価値入率=\frac{売価値入率}{1-売価値入率~~~~~} \) | ○ | ● |
コメント