ROI(Return on Investment) – 投資収益率
最も基本的な ROI の考え方は、投資した金額に対するリターンの構成比率を%(百分率)で考えるところから始まる。
\( \displaystyle \bf ROI=\frac{リターン}{投資額}\times 100\%\)
例えば、100万円を株式に投資して、値上がり益として10万円儲けることができたら、あるいは、1億円でとある事業を始めて、100万円の利益を得ることができたのならば、
\( \displaystyle \bf 株式投資のROI=\frac{~~~~10万円~~~~~~}{100万円}\times 100\%=10\%\)
\( \displaystyle \bf 事業投資のROI=\frac{~~100万円~~~~}{1億円}\times 100\%=10\%\)
となる。
分母に投資額、分子にリターン(得ることができた利益、儲け)を当てはめて、%(パーセント)表示するだけでよい。
分母に対する分子の比率の大きさで儲かり度(収益性)を知ることができる。
これは、会計の世界では、「利益率」とも呼ばれている。
分母に持ってくる数字の性質によって、「売上高利益率」「投資利益率」「総資産利益率」「自己資本利益率」と様々な名前で呼んで識別することができる。
「率」で儲かり度(収益性)を見ることは、投資額の絶対額の大きさをいったん無視して、儲かり度だけで、複数投資案を比較できることを可能にする。
絶対額で儲かり度を評価したい場合は、リターンの絶対額を用いることになる。
しかし、事前に準備できる投資額に一般的には限度が設けられているはずだから(これを予算制約と呼ぶ)、投資対効果が抜群な投資案を優先したいケースには、ROI という評価軸は結構使い勝手が良いものになる。
R:リターンとして考えられる儲け(利益)には2つある
リターン(R: Return)は、投資の見返り(果実)として得られる「儲け」で、会計的には「利益」とも呼ばれる。
(以下では、「利益」という語を用いて説明する)
「利益」には、「総利益(粗利益)」と「純利益」があって、まず最初歩としては、とりあえず手にすることができる儲けを「総利益」と呼び、「総利益」を手にするために犠牲にしなくてはならない経済的価値を差し引いた、最終的に手元に残る儲けを「純利益」と呼ぶ。
このときの犠牲にした経済的価値は、一般的には「コスト」と呼ばれる。
「コスト」の訳語には「原価」か「費用」が当てられることが多いけれど、ここではシンプルに考えるためにカタカナで「コスト」と表記する。
(厳密には「原価」と「費用」とは違う。どうしてもその用語の違いに引っかかってしまう人は、「原価計算基準:三 原価の本質と 五 非原価項目」を読み込んで理解するしかない)
- 「総利益(粗利益)」:とりあえず収入として手元に入る儲け
- 「純利益」:純利益(粗利益)からコストを差し引いた最終的に手元に残る儲け
制度会計における損益計算書(P/L、I/S)では、コストの性質を細かく分けて、差し引くコストの範囲を徐々に広げていくことで、わざといくつかの利益(段階利益)が段階的に表示されるようにしている。
このとき、制度会計ルールでは認識していないコストも、管理会計における採算管理や投資の世界では考慮することになるので、実務的には、制度会計の利益とコスト情報を活用して、投資の世界のリターン、ひいてはROIを計算することになる。
業績評価の分野では、「総利益(粗利益)」を用いることも場合によっては必要になるけれど、投資の世界では、最終的な儲けを問題にすることが基本だから「純利益」を計算に用いることが圧倒的に多くなる。
だから、以降では、特に断りが無ければ、「利益」はコストを差し引いた「純利益」を意味することにする。
そして、投資収益性を判断するうえで、何がコストに含まれているかを考えることが重要になる。
投資の世界の純利益は3段階に分けて考える
純利益は、総利益からいくつかの種類のコストを差し引いたものになる。
ここでは企業体が事業投資から得る純利益をベースに考えることにする。
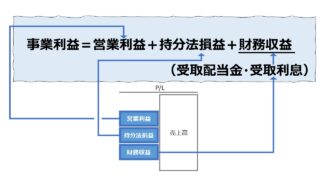
まず、総利益から事業運営に直接かかるコストを差し引いた利益は、呼び名が多種多様に存在するけれど、便宜的に事業利益とここでは呼ぶことにする。
\( \displaystyle \bf 事業利益=総利益-事業コスト\)
または、
\( \displaystyle \bf 事業収益-事業コスト=事業利益\)
次に、そもそも事業を始めるにあたって調達した投資資金を用意するのにかかったコストを「資本コスト」と呼ぶことにして、より厳密に純利益を考えることにする。
\( \displaystyle \bf 純利益=事業利益-資本コスト\)
例:
最初に銀行借り入れで 投資資金を 100 用意する
事業収益 200
事業コスト 190
資本コスト 金利 3%
\( \displaystyle \bf 純利益=事業収益-事業コスト-資本コスト\)
\( \displaystyle \bf 純利益=事業収益-事業コスト-(投資資金\times 3\%)\)
\( \displaystyle \bf 純利益=200-190-(100\times 3\%)\)
\( \displaystyle \bf 純利益=10-3=7\)
\( \displaystyle \bf ROI=\frac{7}{100}\times 100\% =7\%\)
(※ 初期投資が100なのに、事業コストとしてどうして100より大きい190も支出できるのかと疑問を持つ人へ。もしかすると、差額の90は買掛金なのかもしれないし、必要な運転資金は初期投資が2回転して賄っているのかもしれない。要は、資金繰りの工夫次第で、実務としても十分にあり得る設例だということ。)
残念ながら、話はここで終わらない。タックスヘイブンの地域で事業を営んでいたり、特例法で税免除される事業に該当しない限り、儲け(または所得)には税金(法人税や事業税など)がかかってしまう。
それを、ここではまとめて「税金コスト」と呼ぶことにすると、事業投資から最終的に手元に残る税引後の純利益は、
\( \displaystyle \bf 税引後の純利益=事業収益-事業コスト-資本コスト-税金コスト\)
と考えることができる。
ここで、上記設例に、税金コストは、税前利益の20%かかるという条件を加えると、
\( \displaystyle \bf 税引後の純利益=事業収益-事業コスト-資本コスト-税金コスト\)
\( \displaystyle \bf 税引後の純利益=200-190-(100\times 3\%)-税金コスト\)
\( \displaystyle \bf 税引後の純利益=10-3-税金コスト=7-7\times 20\%=7-1.4=5.6\)
\( \displaystyle \bf ROI=\frac{5.6}{100}\times 100\% =5.6\%\)
というふうに計算できる。
計算の世界で扱いが難しい税金コストを何とかする
前章にて、投資利益としての税引後の純利益の概念的算出方法は下記式のようになることは理解できたはず。
\( \displaystyle \bf 税引後の純利益=事業収益-事業コスト-資本コスト-税金コスト\)
しかし、実務においては、「税金コスト」という変数の扱いが難しい。これがいわゆる法人税のように、利益(≒所得)に対する一定税率で求められるとするならば、右辺にある残りの「事業収益」「事業コスト」「資本コスト」の全てが決まった後にしか税金コストを求めることができない。
つまり、この定義式は、実際の計算にそのまま使えないのである。
これを数学的な意味で定義式に設えるためには、右辺の変数は全て独立変数に仕立てる必要がある。
税率を t(上例では20%) と置くと、
\( \displaystyle \bf 税引後の純利益=事業収益-事業コスト-資本コスト-税金コスト\)
\( \displaystyle \bf =事業利益-資本コスト-(事業利益-資本コスト)\times t\)
\( \displaystyle \bf =(事業利益-資本コスト)\times(1-t)\)
\( \displaystyle \bf =事業利益 \times(1-t) -資本コスト \times(1-t)\)
\( \displaystyle \bf =税引後事業利益 -(1-t)\times資本コスト\)
と整理できる。
資本コストは、事業利益の多寡に関係なく、投資額と資本コスト率の積で独立的に表すことができるので、この定義式は数学的にきちんと成立している。
(※ 資本コストは、事業収益や事業コストとは無関係に事前に準備する資金の資本構成に依存して決まる)
一気呵成にROICとEPにまで辿り着く
これ以上の分解とアルファベットによる変数表記は純利益の計算のためには不要だが、敢えて資本コスト率を r、調達資本額を I と置けば、
\( \displaystyle \bf 純利益=税引後事業利益-(1-t)(r\times I) \)
\( \displaystyle \bf 純利益=税引後事業利益-(1-t)r\times I \)
ここで、法人税考慮後の資本コスト率を r’=(1-t)r と置くと、
\( \displaystyle \bf 純利益=税引後事業利益-(1-t)r\times I \)
\( \displaystyle \bf 純利益=税引後事業利益-r’\times I \)
と示すことができる。
この式は、変数の表記を変えてやるだけでよく目にする有名な定義式に様変わりする。
純利益をEP(Economic Profit)、税引後事業利益をNOPAT(Net Operating Profit after Taxes)、r’をWACC(Weighted Average Cost of Capital: 加重平均資本コスト)と置き換えると、
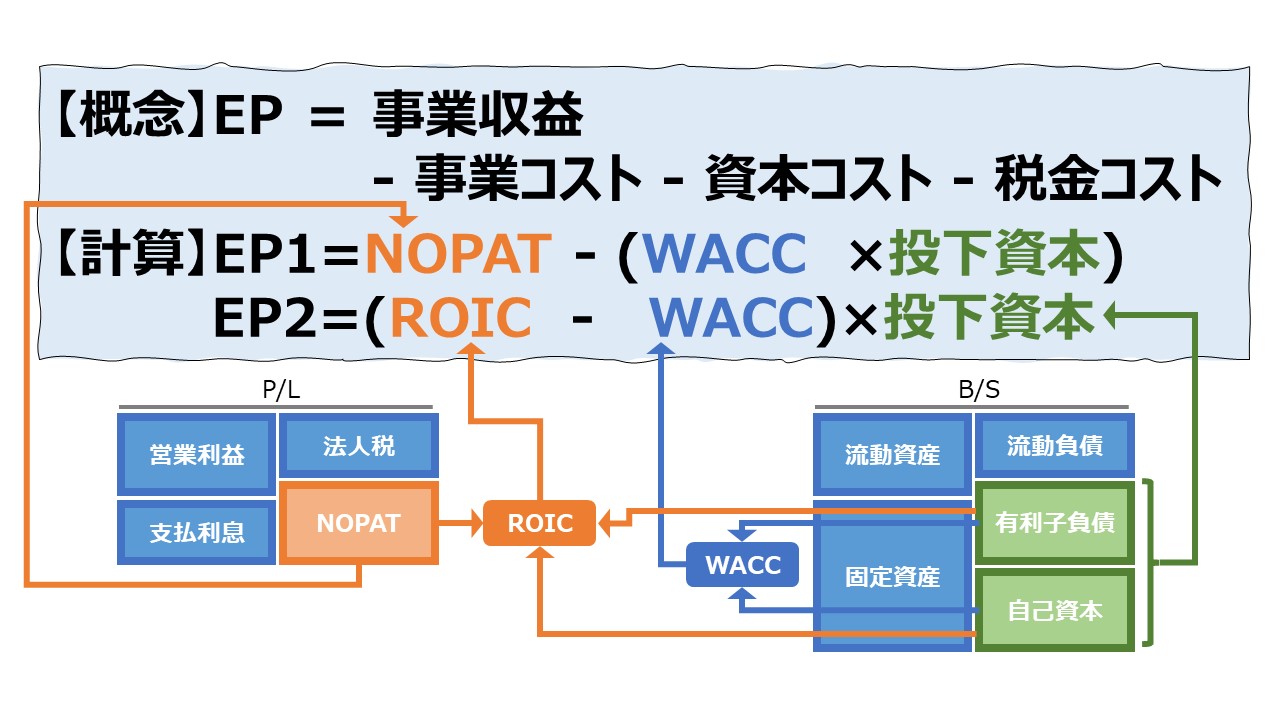
\( \displaystyle \bf EP=NOPAT-WACC\times投下資本 \)
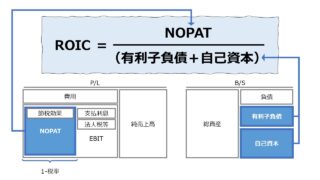
さらに、いきなり何もないところからこの定義を導出するのには無理があるが、NOPATを用いたROIの特殊解として、ROIC(Return on Invested Capital: 投下資本利益率)を下記のように表現することができると考えると、
\( \displaystyle \bf ROIC=\frac{NOPAT}{投下資本} \)
\( \displaystyle \bf NOPAT=ROIC \times 投下資本 \)
この定義式をEPの式に代入して、
\( \displaystyle \bf EP=NOPAT-WACC\times投下資本 \)
\( \displaystyle \bf EP=(ROIC \times 投下資本) -WACC\times投下資本 \)
\( \displaystyle \bf EP=(ROIC-WACC)\times投下資本 \)
としてまとめることができる。
(※ 厳密には、提唱者によればEPにはNOPATよりNOPLAT(Net Operating Profit Less Adjusted Taxes: みなし税引後営業利益)という呼称の方がふさわしいそうだ)
- 概念的には、EPは事業収益から事業コストと資本コストと税金コストを控除したものである
- 実務的には、EPはNOPATと税効果考慮後の資本コストを用いて計算する
資本コスト率をWACCとわざわざ表記するのには訳がある。負債(他人資本)におけるタックスシールドによる影響を考慮した後のものであることに注意を払うためだ。
WACCの算出方法とEPの使いどころについては別稿で説明する。

コメント