- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
CAPMの計算式 CAPM Formula
計算式の解説
資本資産価格モデル（CAPM）は、❶個々の証券または投資ポートフォリオのシステマティック・リスク（いわゆるβ値）、❷市場全体の期待収益率、❸リスクフリーレートを用いて、投資家による個々の証券投資や投資ポートフォリオの必要収益率（目標収益率）を決定する。
CAPM理論が背景にあって、個々の証券投資や投資ポートフォリオの期待収益率が必要収益率（目標収益率）にサヤ寄せされて一致するように投資対象証券の値付けを行うし、必要収益率（目標収益率）はリスクフリーレートにリスクプレミアムが加算された値になるようも証券価格の値付けを行う。リスクプレミアムは、投資対象証券が持つシステマティック・リスク（β値）によって自ずとその水準が定まるものである。
とりあえず、CAPMの計算式は次のように表すことができる。
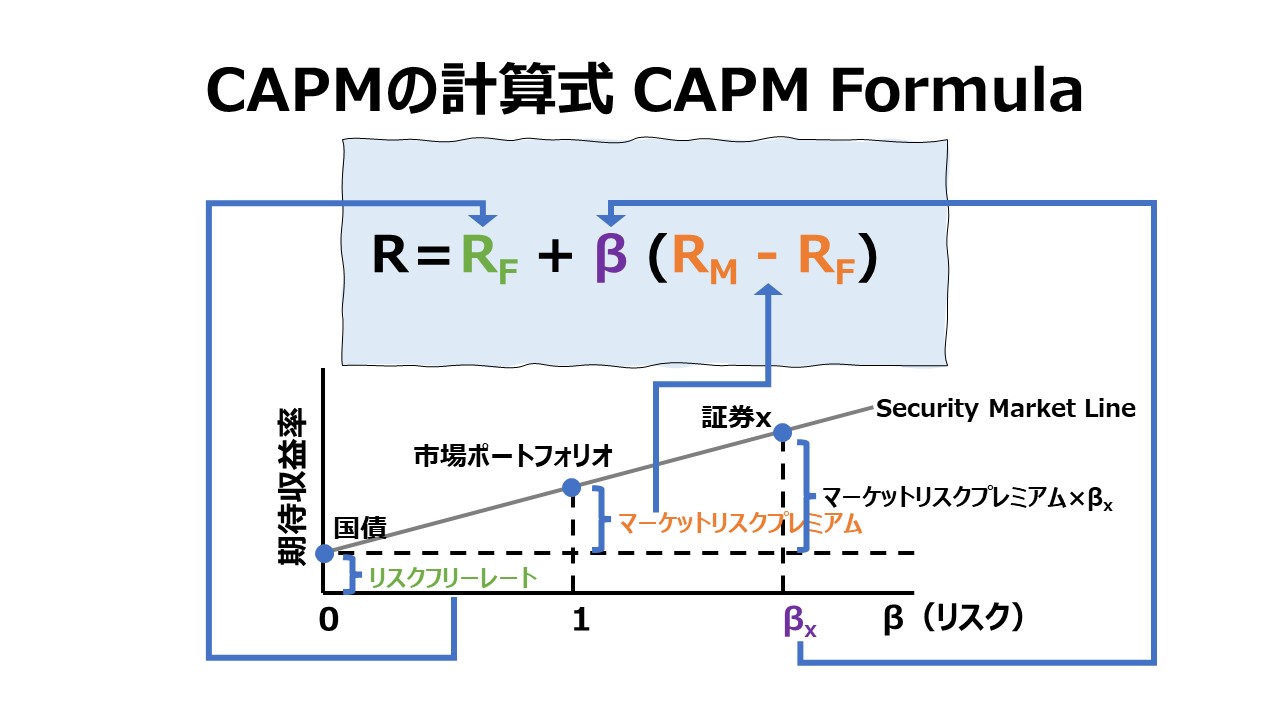
\( \displaystyle \bf R=R_F+β(R_M-R_F) \)
- R: 投資家の必要利益率（目標利益率）
- RF：リスクフリーレート
- β: β値
- RM: 市場全体の期待収益率
リスクフリーレート（RF）は、投資家が安全資産から得ることができる収益率のことを指し、一般的には、短期米国債（short-term U.S. treasury securities）で代表される。
市場全体の期待収益率（RM）は、株式市場における平均的な収益率のことを指し、一般的には、S&P500や日経平均株価・TOPIXといったインデックス指標に基づいて計算される。
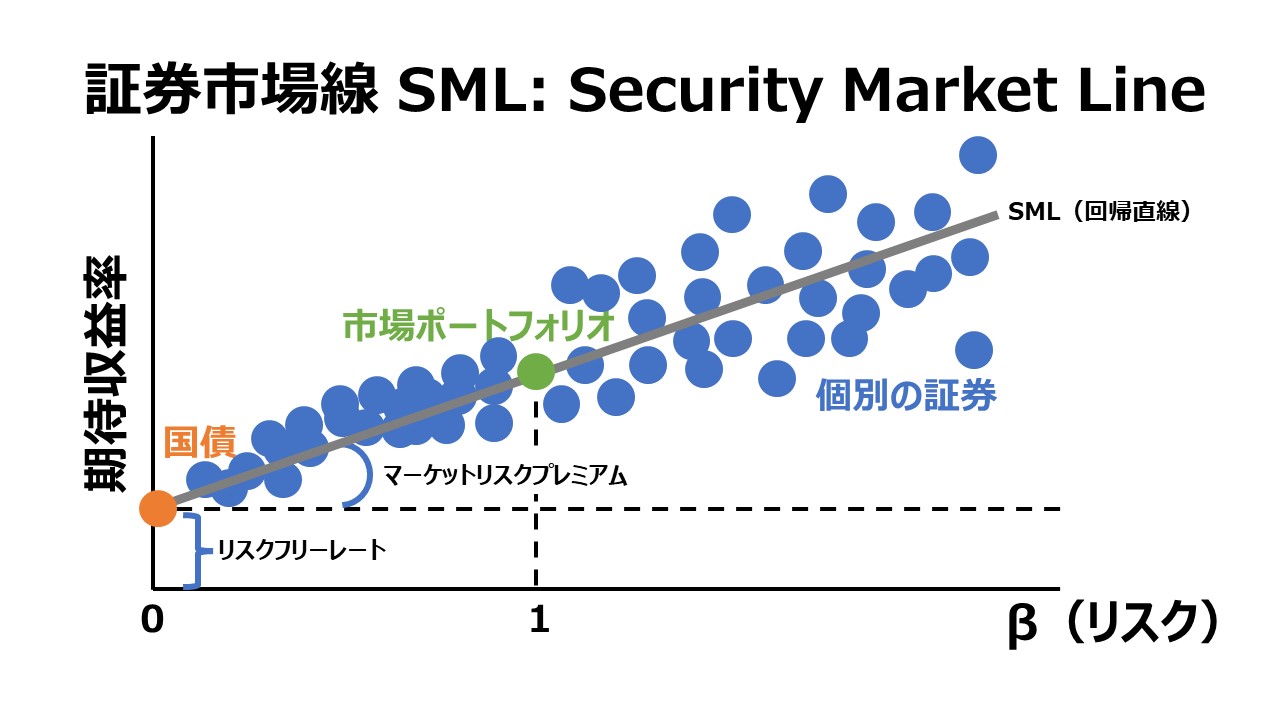
市場全体の期待収益率とリスクフリーレートの差額（RM-RF）は、マーケット・リスクプレミアムと呼ばれる。マーケット・リスクプレミアムは、株式市場の超過収益力を測定するものであり、大抵はリスクフリーレート（RF）よりRMが大きくなることで正の値になる。
このマーケット・リスクプレミアムが正の値を持ち、その正の値が大きくなればなるほど、投資家がその株式市場へ投資をしてもよいと考える誘因を強くする。
ただし、このマーケット・リスクプレミアムそれ自体は、投資家が実際に投資対象に選定する個別証券または投資ポートフォリオの期待収益率をそのままでは代表しない。マーケット・リスクプレミアムは市場全体のものだから、個別証券や投資ポートフォリオはその中に含まれているに過ぎないと理解すべきものである。
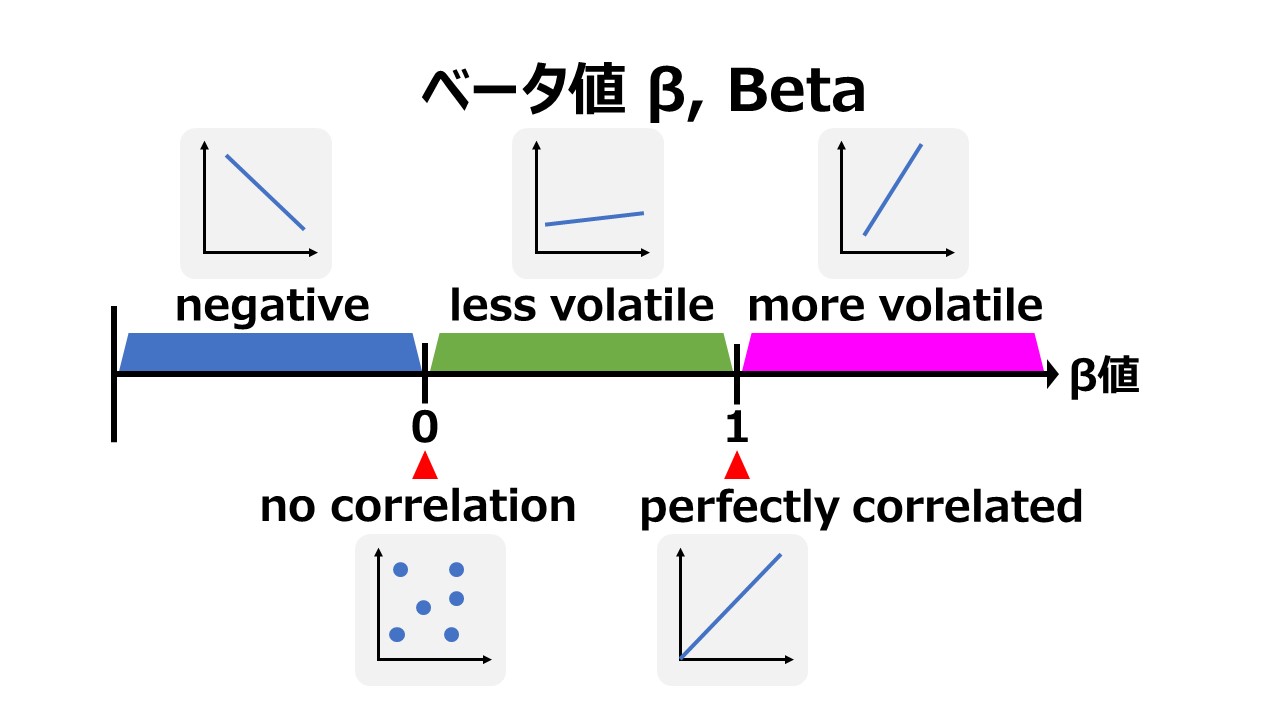
β値は、個別証券または投資ポートフォリオの過去実績の収益率と市場全体の過去実績の収益率の相関関係を示す。この時の”市場全体”は、S&P500、日経平均株価、TOPIXといったインデックス指標で表されることになる。
β値は、株式市場全体の収益率の変化に対して個別証券または投資ポートフォリオの収益率の変化の感応度を測定するものである。
ある意味、個別証券または投資ポートフォリオのβ値は、株式市場全体のリスクに対する個別証券または投資ポートフォリオが持つ限界収益率と理解することもできる。
β(RM-RF)は、個々の証券投資や投資ポートフォリオのリスクプレミアムを表す。この時のリスクプレミアムの意味は、その個別証券や投資ポートフォリオを購入したり投資したりするために相応しい（必要な）収益率（期待リターン）のことを指す。
当然、高いβ値（高いリスクプレミアム）には高いリターン（期待収益率）が対応することになる。
以上のことから、特定の証券や投資ポートフォリオへの投資から期待される収益率（R）というものは、リスクフリーレート（RF）にその投資対象のリスクプレミアム β(RM-RF) を足したものになる。
シミュレーション
Excelテンプレート形式でCAPMに基づく投資対象の期待収益率の計算方法を示す。
入力欄の青字になっている「リスクフリーレート」「株式市場の要求収益率」「投資対象のβ値」に任意の数字を入力すると、投資対象の要求収益率がCAPM計算式に従って自動的に算出されるとともに、グラフを自由に操作することができる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
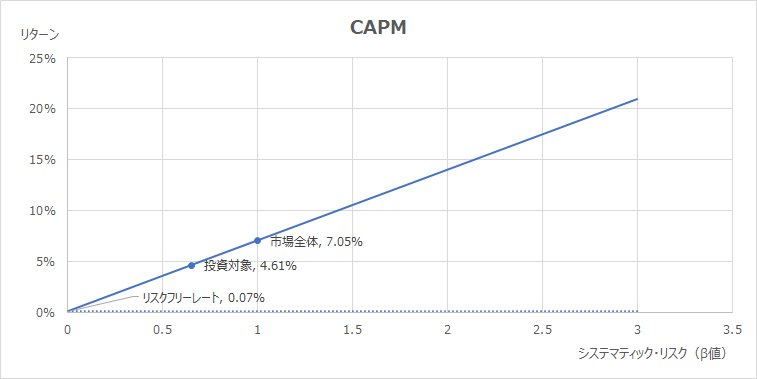
上記のサンプル指標は、2021年11月22日時点の新発10年国債利回り：0.070%をリスクフリーレート、日経平均の株式益回り：7.05%を株式市場の要求収益率、トヨタ自動車の3年（~2021年10月）平均の日経平均に対するβ値：0.65を投資対象のβ値として設定したものである。
実際には、株式益回りはPERの逆数として、同日のPERから求めている。
ちなみに、上で求めた投資対象の要求収益率は4.61%となっているが、同日のトヨタ自動車のリアルな株式益回りである期待収益率は8.54%と、約1.9倍の開きがある。
同じCAPMモデルを用いて、同日の武田薬品工業の要求収益率（理論株式益回り）は、7.61%と試算されたが、実際の同日同社のリアルな株式益回りは3.67%であり、理論値の約48%にとどまっている。
サンプリングはこの2社だけなので、十分な数とは決して言えないが、βが1を超える景気敏感株の場合は、理論値を1/2し、βが1を下回るディフェンシブ株の場合は、理論値を2倍すると、リアルな数値の近似値を採ることができる可能性がある。
実務においては、長期にわたった観察により、こうした補正項は、帰納的に求める他仕方がないものである。
いずれにせよ、たった2つのサンプルだけでも、βの大小と株式益回りの関係に矛盾が起きずに一定程度の仮説に収まって筆者自身、胸をなでおろしているところだ。
【参考】使用しているExcel関数
特になし
コメント