- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
Excelテンプレート
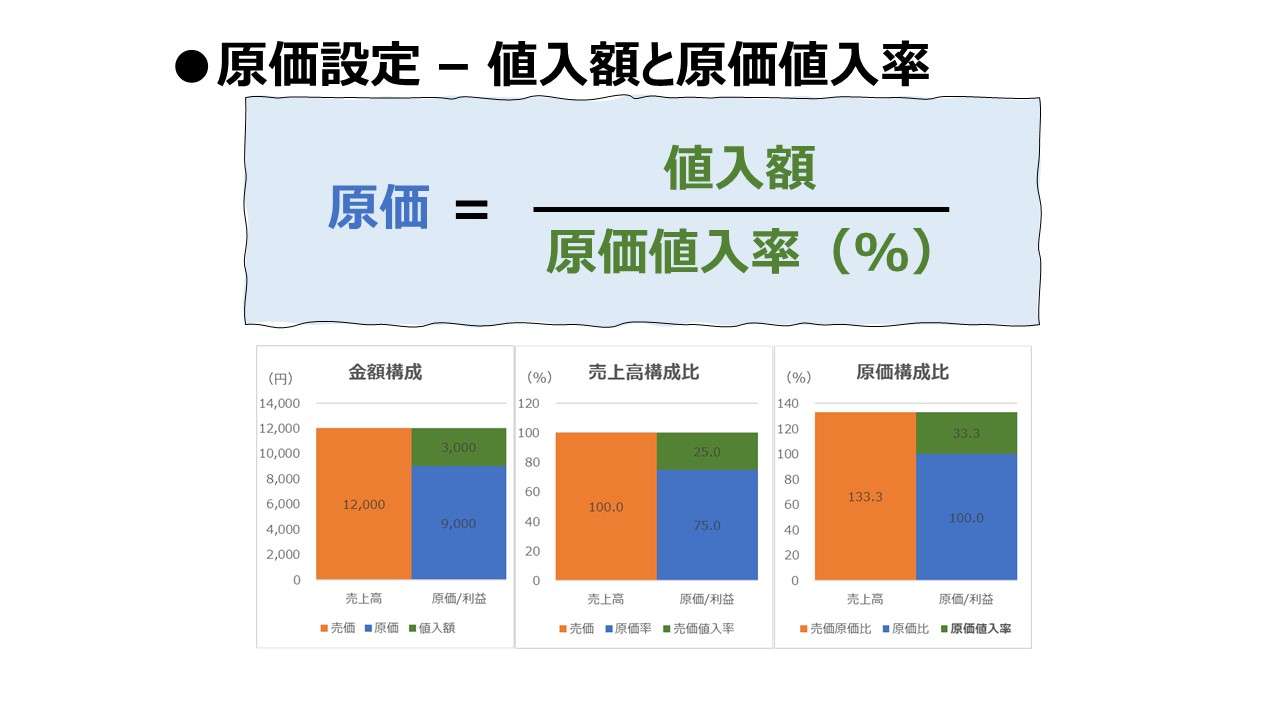
- 値入額と原価値入率から原価を求める。
計算式
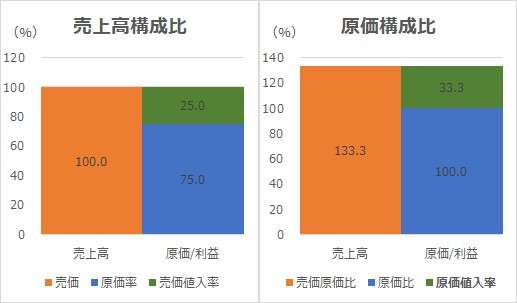
\( \displaystyle \bf 原価=\frac{値入額}{原価値入率}\)
例）
\( \displaystyle \bf 原価= \frac{20}{25\%} = 80 \)
式展開）
\( \displaystyle \bf 原価値入率 = \frac{値入額}{原価} \)
\( \displaystyle \bf \frac{値入額}{原価} = 原価値入率 \)
両辺の分子分母をひっくり返して、
\( \displaystyle \bf \frac{原価}{値入額} = \frac{1}{原価値入率} \)
両辺に値入額を掛けると、
\( \displaystyle \bf 原価 = \frac{値入額}{原価値入率} \)
説明
入力欄の青字になっている「値入額」「原価値入率」に任意の数字を入力すると、表とグラフを自由に操作することができる。
この式は、所定の希望利益額（≒値入額）と、希望利益率（＝原価値入率）の両立を図ることができる原価の額を求めようとする場合の基本式である。
類似の公式に、
\( \displaystyle \bf 原価=値入額\times\left(\frac{1}{売価値入率}-1\right)\)
がある。いずれも、利益額と利益率で原価を求める式であるが、売価値入率の方は、いったん売価ベースで値入率を考えるところから、計算式の組成が複雑になる。
（※その一方で、売価利益率（ROS：売上高利益率）の概念の方が一般的でよく用いられる）
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
特になし
原価設定
| # | 計算式 | Excelテンプレート |
|---|---|---|
| ❽ | \( \displaystyle \bf 原価=売価-値入額 \) |  原価設定 売価と値入額 |
| ⑨ | \( \displaystyle \bf 原価=売価\times原価率 \) |  原価設定 売価と原価率 |
| 10 | \( \displaystyle \bf 原価=売価\times(1-売価値入率) \) |  原価設定 売価と売価値入率 |
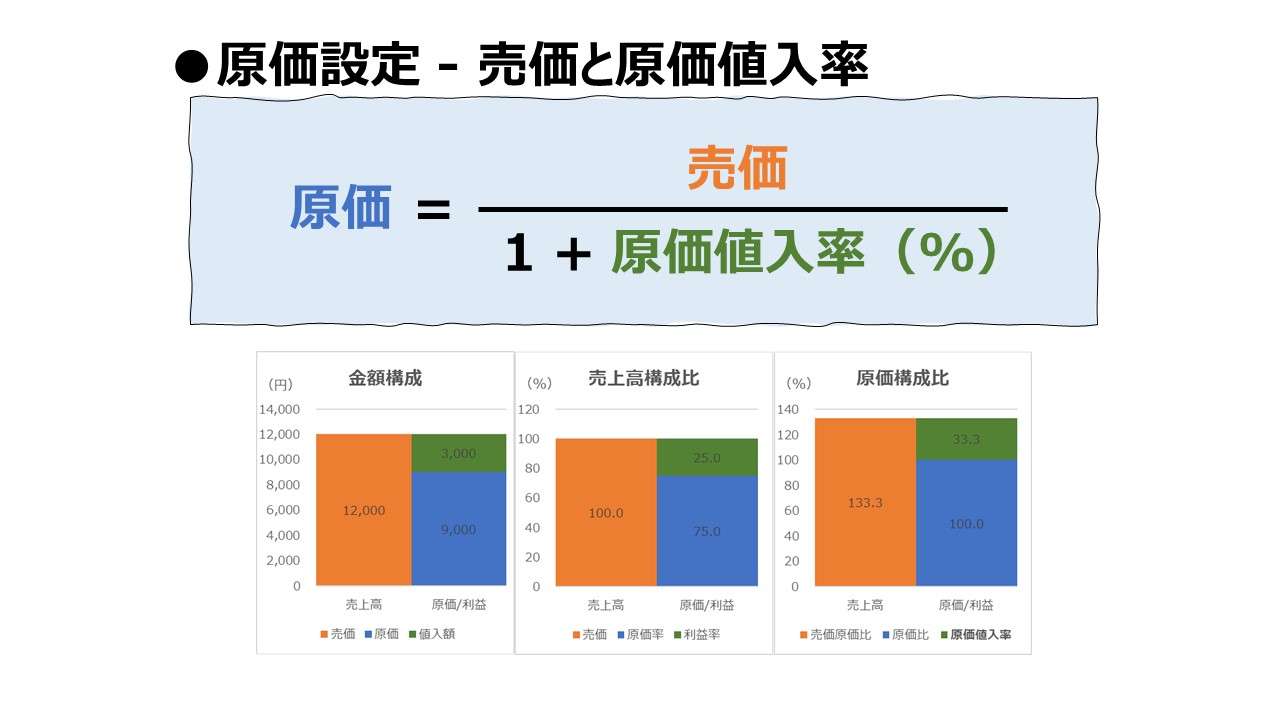
| 11 | \( \displaystyle \bf 原価=\frac{~~~~~~~~~~~~売価~~~~~~~~~~~~~~~}{(1+原価値入率)~~~~~}\) |  原価設定 売価と原価値入率 |
| ⑫ | \( \displaystyle \bf 原価=\frac{値入額}{原価値入率}\) |  原価設定 値入額と原価値入率 |
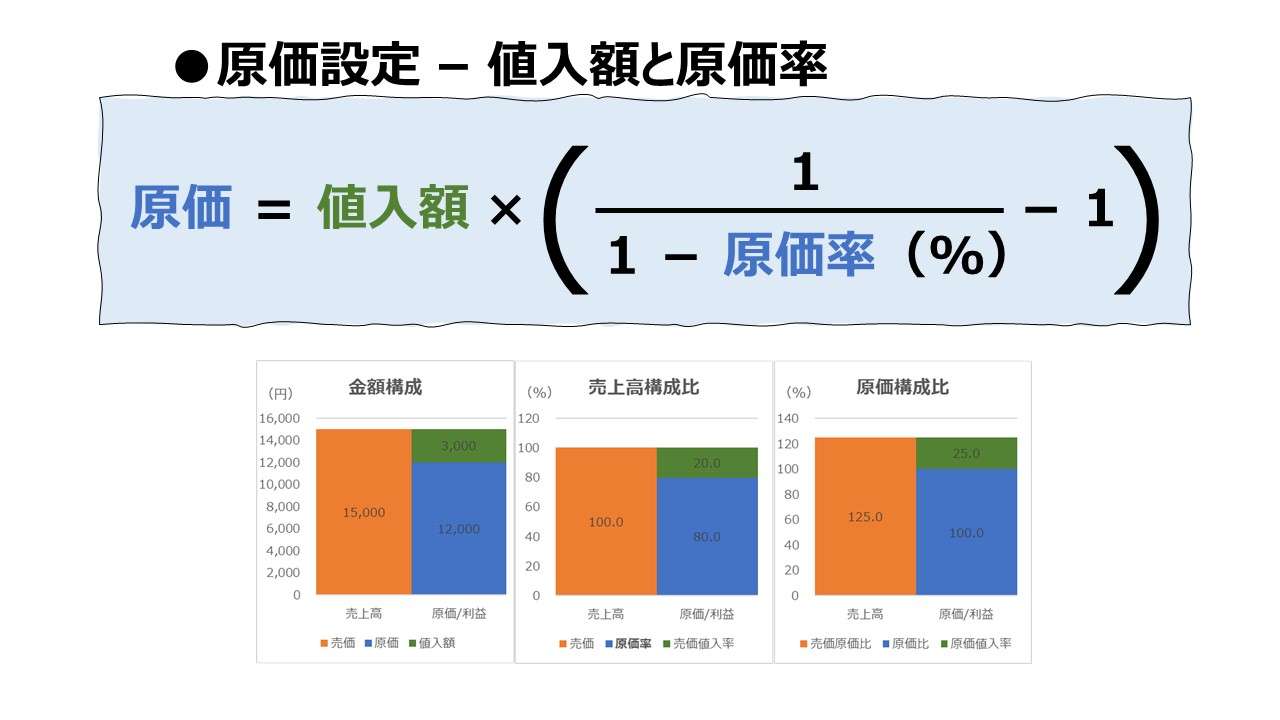
| 13 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{1-原価率~~~~~}-1\right)\) |  原価設定 値入額と原価率 |
| 14 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{売価値入率}-1\right)\) |  原価設定 値入額と売価値入率 |
公式一覧
| # | 計算式 | 売価 | 原価 | 値入額 | 原価率 | 売価値入率 | 原価値入率 |
|---|---|---|---|---|---|---|---|
| ❶ | \( \displaystyle \bf 売価=原価+値入額 \) | ● | ○ | ○ | |||
| ② | \( \displaystyle \bf 売価=\frac{原価}{原価率}\) | ● | ○ | ○ | |||
| 3 | \( \displaystyle \bf 売価=\frac{~~~~~~~~~~原価~~~~~~~~~~~~~~~}{1-売価値入率~~~~~}\) | ● | ○ | ○ | |||
| 4 | \( \displaystyle \bf 売価=原価\times(1+原価値入率) \) | ● | ○ | ○ | |||
| ⑤ | \( \displaystyle \bf 売価=\frac{値入額}{売価値入率}\) | ● | ○ | ○ | |||
| 6 | \( \displaystyle \bf 売価=\frac{~~~~~~~~値入額~~~~~~~~~~~}{1-原価率~}\) | ● | ○ | ○ | |||
| 7 | \( \displaystyle \bf 売価=値入額\times\left(\frac{1}{原価値入率}+1\right)\) | ● | ○ | ○ | |||
| ❽ | \( \displaystyle \bf 原価=売価-値入額 \) | ○ | ● | ○ | |||
| ⑨ | \( \displaystyle \bf 原価=売価\times原価率 \) | ○ | ● | ○ | |||
| 10 | \( \displaystyle \bf 原価=売価\times(1-売価値入率) \) | ○ | ● | ○ | |||
| 11 | \( \displaystyle \bf 原価=\frac{~~~~~~~~~~~~売価~~~~~~~~~~~~~~~}{(1+原価値入率)~~~~~}\) | ○ | ● | ○ | |||
| ⑫ | \( \displaystyle \bf 原価=\frac{値入額}{原価値入率}\) | ● | ○ | ○ | |||
| 13 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{1-原価率~~~~~}-1\right)\) | ● | ○ | ○ | |||
| 14 | \( \displaystyle \bf 原価=値入額\times\left(\frac{1}{売価値入率}-1\right)\) | ● | ○ | ○ | |||
| ⓯ | \( \displaystyle \bf 値入額=売価-原価 \) | ○ | ○ | ● | |||
| ⑯ | \( \displaystyle \bf 値入額=売価\times売価値入率 \) | ○ | ● | ○ | |||
| 17 | \( \displaystyle \bf 値入額=売価\times(1-原価率) \) | ○ | ● | ○ | |||
| 18 | \( \displaystyle \bf 値入額=\frac{売価}{\frac{1}{原価値入率}+1} \) | ○ | ● | ○ | |||
| ⑲ | \( \displaystyle \bf 値入額=原価\times原価値入率 \) | ○ | ● | ○ | |||
| 20 | \( \displaystyle \bf 値入額=原価\times\left(\frac{1}{原価率}-1\right) \) | ○ | ● | ○ | |||
| 21 | \( \displaystyle \bf 値入額=\frac{原価}{\frac{1}{売価値入率}-1} \) | ○ | ● | ○ | |||
| ㉒ | \( \displaystyle \bf 原価率=\frac{原価}{売価} \) | ○ | ○ | ● | |||
| 23 | \( \displaystyle \bf 原価率=1-\frac{値入額}{売価} \) | ○ | ○ | ● | |||
| 24 | \( \displaystyle \bf 原価率=1-売価値入率 \) | ● | ○ | ||||
| 25 | \( \displaystyle \bf 原価率=\frac{1}{1+\frac{値入額}{原価}}\) | ○ | ○ | ● | |||
| 26 | \( \displaystyle \bf 原価率=\frac{1}{1+原価値入率~~~~~}\) | ● | ○ | ||||
| ㉗ | \( \displaystyle \bf 売価値入率=\frac{値入額}{売価}\) | ○ | ○ | ● | |||
| 28 | \( \displaystyle \bf 売価値入率=1-\frac{原価}{売価}\) | ○ | ○ | ● | |||
| 29 | \( \displaystyle \bf 売価値入率=1-原価率\) | ○ | ● | ||||
| 30 | \( \displaystyle \bf 売価値入率=\frac{1}{\frac{原価}{値入額}+1} \) | ○ | ○ | ● | |||
| 31 | \( \displaystyle \bf 売価値入率=\frac{原価値入率}{1+原価値入率~~~~~} \) | ● | ○ | ||||
| ㉜ | \( \displaystyle \bf 原価値入率=\frac{値入額}{原価} \) | ○ | ○ | ● | |||
| 33 | \( \displaystyle \bf 原価値入率=\frac{売価}{原価}-1 \) | ○ | ○ | ● | |||
| 34 | \( \displaystyle \bf 原価値入率=\frac{1}{原価率}-1 \) | ○ | ● | ||||
| 35 | \( \displaystyle \bf 原価値入率=\frac{1}{\frac{売価}{値入額}-1} \) | ○ | ○ | ● | |||
| 36 | \( \displaystyle \bf 原価値入率=\frac{売価値入率}{1-売価値入率~~~~~} \) | ○ | ● |
コメント