- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算手法
NPV法そのものの超概念は、「正味現在価値法（NPV法: Net Present Value Method）- 不定額回収」にて詳細を説明している。
概要
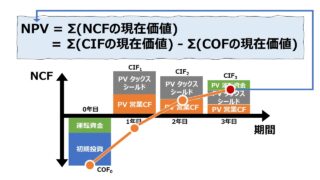
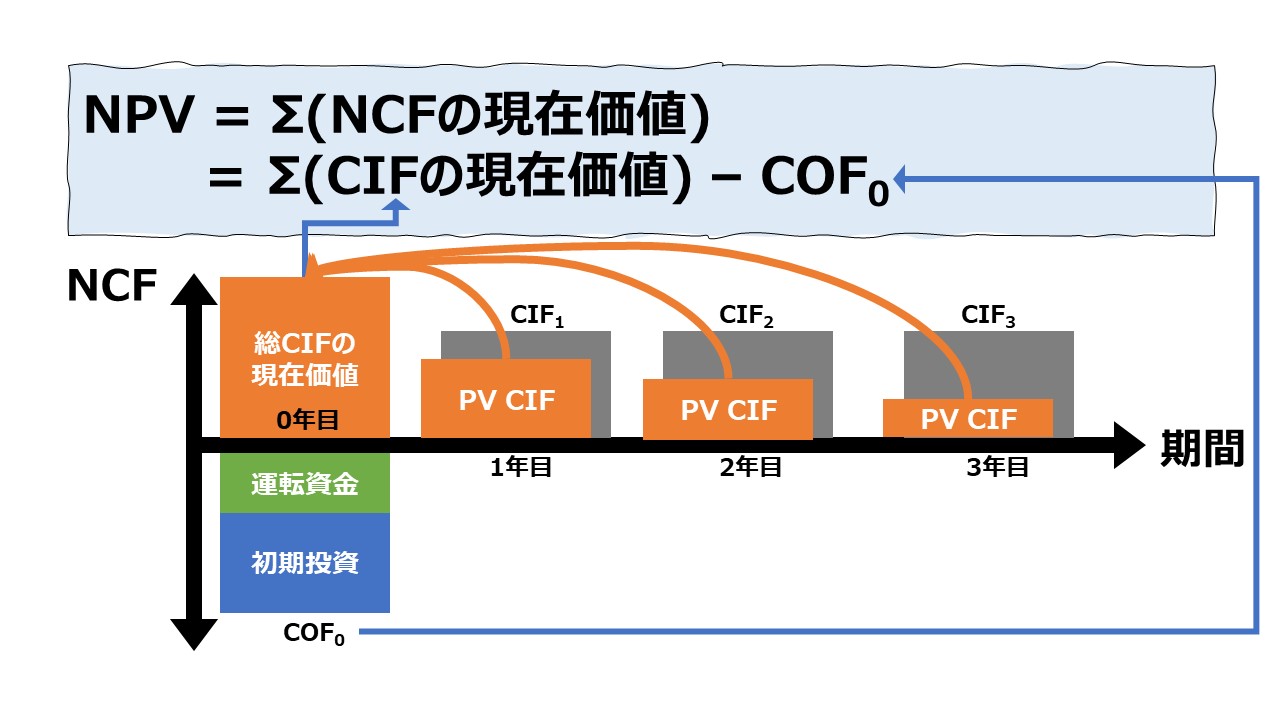
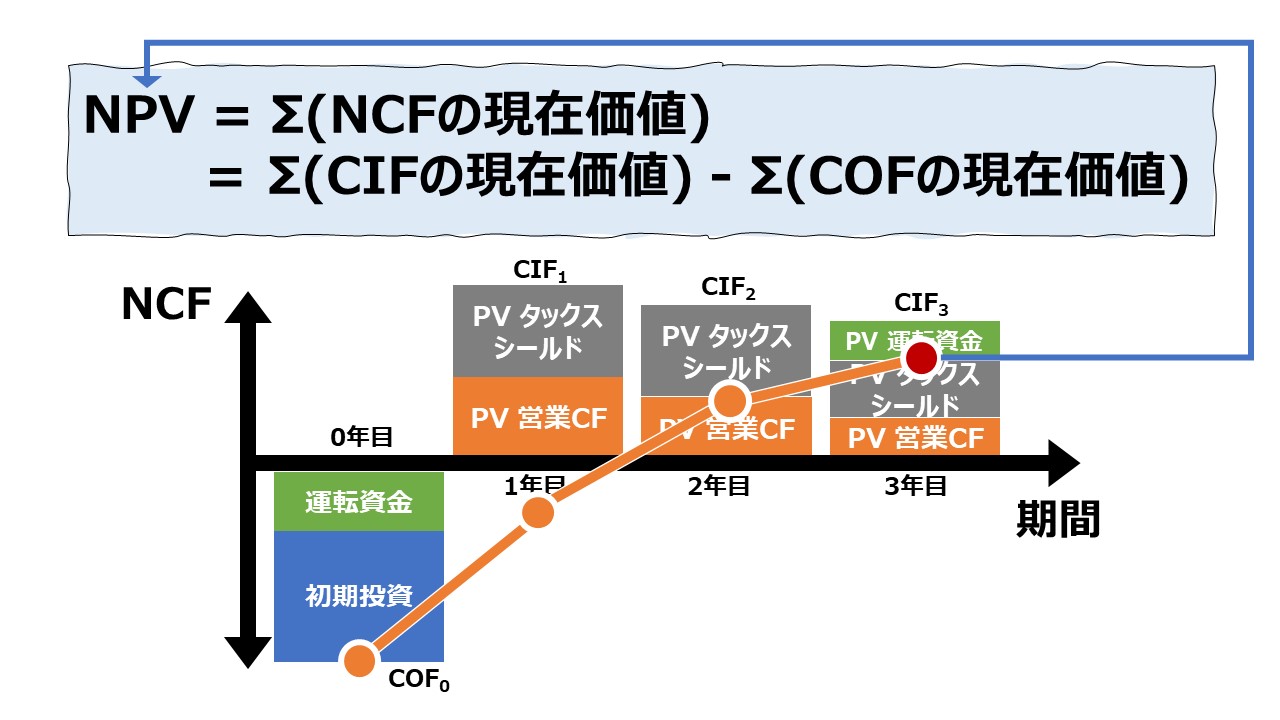
正味現在価値法（NPV: Net Present Value Method）は、投資案件やプロジェクトからの全てのキャッシュ・イン・フローとキャッシュ・アウト・フローを割引率を用いて現在価値に置き換えた合計値で投資案件やプロジェクト全体の採算を評価する手法である。
プロジェクト期間（投資期間）の各会計期において、それぞれ異なる金額（キャッシュ・イン・フロー：CIF）で投資回収が行われた場合、各期のCIFから個別に割引現在価値を算出してから最後に合計して、プロジェクト（投資案件）全体のNPVを導き出す。
一方で、プロジェクト期間（投資期間）を通じて、毎期一定額のCIFで投資回収できる場合、毎期一定額のCIFの額と割引率が分かれば、即時にプロジェクト（投資案件）全体のNPVを計算することができる。
●不定額回収のケース
- プロジェクトプロファイル情報を洗い出す
- 初期投資額
- 投資期間
- 割引率
- 各期ごとの投資回収額
- 各期の投資回収額の割引現在価値を求める
- 各期の割引現在価値を集計する
- 上記集計額から初期投資額を引いてNPVを算出する
●定期回収のケース
- プロジェクトプロファイル情報を洗い出す
- 初期投資額
- 投資期間
- 割引率
- 各期共通の投資回収額
- 投資回収総額の割引現在価値を求める
- 上記額から初期投資額を引いてNPVを算出する
各期とプロジェクト全体の割引現在価値の算出方法の違い
「現価係数」で各期回収額の割引現在価値を求める
各期ごとの回収額に現価係数を乗じることで、各期ごとに異なる回収額の割引現在価値を算出できる。
該当年数をn、割引率をr とおくと、
\( \displaystyle \bf 現価係数＝\frac{1}{(1+r)^n}\)
- 初期投資額：100
- 投資期間：2年
- 割引率：10%
- 1年目回収額：55
- 2年目回収額：60.5
\( \displaystyle \bf 1年目回収額の現在価値＝55\times\frac{1}{(1+0.1)^1}\)
\( \displaystyle \bf ＝\frac{55}{1.1}=50\)
\( \displaystyle \bf 2年目回収額の現在価値＝60.5\times\frac{1}{(1+0.1)^2}\)
\( \displaystyle \bf ＝\frac{60.5}{1.21}=50\)
\( \displaystyle \bf NPV＝1年目回収額の現在価値+2年目回収額の現在価値-初期投資額\)
\( \displaystyle \bf NPV＝50+50-100=0\)
「年金現価係数」で投資回収総額の割引現在価値を求める
投資回収総額＝共通回収額×回収期間なので、共通回収額が分かれば投資回収総額が分かるはず。
共通回収額に年金現価係数を乗じることで、投資回収総額としての割引現在価値を計算することができる。
投資期間（年数）をn、割引率をr とおくと、
\( \displaystyle \bf 年金現価係数＝\frac{(1+r)^n-1}{r(1+r)^n}\)
- 初期投資額：100
- 投資期間：2年
- 割引率：10%
- 定期回収額：57.619
\( \displaystyle \bf 投資回収総額の現在価値＝定期回収額\times \frac{(1+r)^n-1}{r(1+r)^n} \)
\( \displaystyle \bf ＝57.619 \times \frac{(1+0.1)^2-1}{0.1(1+0.1)^2} \)
\( \displaystyle \bf ＝57.619 \times \frac{(1.1)^2-1}{0.1(1.1)^2} \)
\( \displaystyle \bf ＝57.619 \times \frac{1.21-1}{0.1\times1.21} \)
\( \displaystyle \bf ＝\frac{ 57.619 \times 0.21}{0.121}= \frac{12.0999}{0.121} =99.999\)
\( \displaystyle \bf NPV＝投資回収総額の現在価値-初期投資額\)
\( \displaystyle \bf NPV＝99.999-100≒0\)
年金現価係数の公式の内容が文系人間にとって直観的には分からないので、同様のシンプル例につき、各期の回収額と現価係数からNPVを求めてみる。
\( \displaystyle \bf 1年目回収額の現在価値＝57.619\times\frac{1}{(1+0.1)^1}\)
\( \displaystyle \bf ＝\frac{57.619}{1.1}=52.3809\)
\( \displaystyle \bf 2年目回収額の現在価値＝57.619\times\frac{1}{(1+0.1)^2}\)
\( \displaystyle \bf ＝\frac{57.619}{1.21}=47.619\)
\( \displaystyle \bf NPV＝1年目回収額の現在価値+2年目回収額の現在価値-初期投資額\)
\( \displaystyle \bf NPV＝52.3809+47.619-100=99.999-100≒0\)
Excel の PV関数を用いて計算する
とにかく、計算ロジック（理屈）はややこしく、年金現価係数の公式を端から暗記する気力が湧かないので、手っ取り早く結果だけほしい人には、おあつらえ向きに、「PV関数」が用意されている。
（※類似のものに「NPV関数」「XNPV関数」もある。「NPV関数については、「正味現在価値法（NPV法: Net Present Value Method）- 不定額回収」で下記と同様の解説をしている）
そして、機械的に数字を当てはめても期待通りの結果が得られない可能性も高い。
PV関数の使い方はシンプルである。上記と同じ例を用いれば、次のように記述することができる。
=PV(割引率,投資期間,–定期回収額)
初期投資額をPV関数の外から引いてやると、
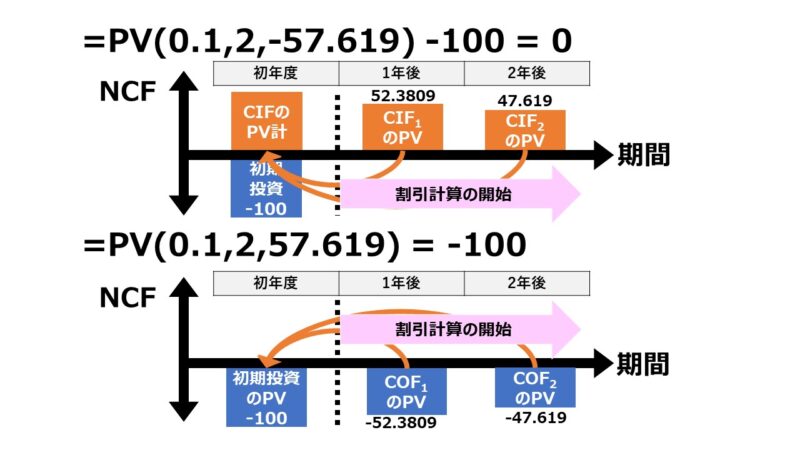
=PV(0.1,2,-57.619)-100 ≒ 0 →意図通りに計算された
そのまま機械的にPV関数を（おそらくは意図に反して）使ってしまうと、
PV(0.1,2,57.619) = -99.999917… ≒-100
計算結果から、２つの違和感があるはず。
❶ 意図したゼロにならずに絶対値100を示す値になっている
❷ その絶対値の符号がマイナスになっている
❶について
PV関数で計算される値は、割引計算対象範囲のものだけである。初期投資額は、割引計算対象外なので、PV関数の外から反映してやる必要がある。
❷について
PV関数（Excel財務関数に共通して言えるお約束だが）の使い方として、入力する数（引数）と計算結果として表示される数（戻り値）の符号は逆になる。
毎月同額を定期積立する場合は、毎月は定額のCOF（マイナス）になり、積立満期時に元利金が手許に戻ってくる（CIFで符号はプラス）。
逆に、毎月同額が借りられる（CIF）という条件の借入金は、返済期限になったら元利金を完済（COF）する必要がある。
PV関数を使用してプロジェクト（投資案件）の投資採算を評価するならば、イメージとしては借入金パターンで、毎期の回収額（CIF）が、初期投資額（COF）を上回ることを目指す。
その他の資本予算の構成について
☞NCFの意味を確認するには、下記稿を参考にするとよい。
☞各期の抽出すべき取引内容を確認するには、下記稿を参考にするとよい。
☞割引現在価値を求めるための、❶年利、❷回収期間、❸回収額の関係を知るためには、下記稿を参考にするとよい。
計算プロセス
定額回収による正味現在価値法（NPV法）の計算プロセスは、基本的に 「正味現在価値法（NPV法: Net Present Value Method）- 不定額回収」と同じである。
不定額と定額の違いから、各期の回収額を集計するというステップのひとつを省略することができる。
- 初期投資額の計算初期投資額を明らかにする
・設備投資などの初期投資額
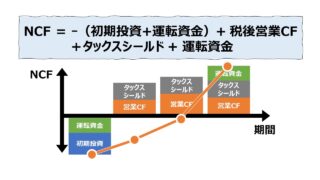
- 回収NCFの計算各期の定額回収NCFを計算する
・CIFとCOFを相殺した正味（ネット）額を計算する
・税引後で計算する - 割引率の設定各期の定額回収額を現在価値に置き換えるための割引率を設定する
・各期共通の定額回収額を現在価値に割り引くための予定利率を想定する
・年利で求めれば回収期間の単位は年になる - NPVの算出各期定額回収額の割引現在価値（NPV）を求める
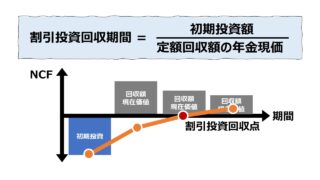
・NPV=定額回収額×年金現価係数
・年金現価係数は、割引率と投資期間で一意に決まる - 投資採算性の判断NPVの正負の大きさで、投資収益性を判定する
・ NPV＞０ならば、投資額を上回る価値を創出していると判断できる
NPVの計算自体は、Excel関数も存在することから、Excel関数を意図に反して使ってしまう（❶初期投資額を反映するのを忘れない、❷定期回収額はマイナス値で入力する）ことだけ注意しておけば、大した手間もかからずあっけないぐらい簡単に計算することができる。
大事なことは、そのNPV計算にかけるべき初期投資額を構成する要素の洗い出しと妥当な定期回収額の決定の方であり、かかる手間暇もほぼこれが99%を占めるものと思われる。
シミュレーション
Excelテンプレート形式で各期定額の投資回収が見込める場合の正味現在価値（NPV）を求める計算方法を示す。
入力欄の青字になっている「初期投資額」「定期回収額」「回収期間」 「割引率」 に任意の数字を入力すると、年金現価係数（PV関数）を用いた正味現在価値（NPV）が求められる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
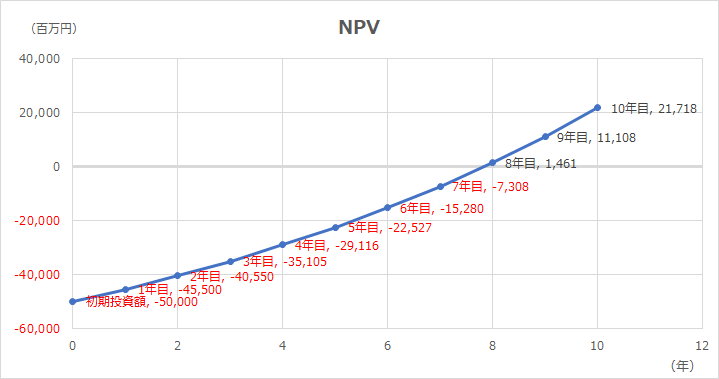
グラフの見方
Excelの散布図グラフを用いてグラフ表示している。
横軸は経過年を示しており、0.0年（ゼロ年）が初期投資した時点で、投資期間が最長（終期）となる。
途中経過年（経過点）は、一律10等分で自動計算されている。仮に投資期間が20年ならば、2年ごとのプロットとなる。10年未満の場合は、1.5年など、年数に対して小数点表示となる。
定額回収のため、年数が経過するにつれて複利効果が次第に大きくなるので、下に凸の（下方に膨らむ）曲線を描く。
時間が長くなればなるほど、割引率（裏返すと時間の利益、金利みたいなもの）の効果が大きくなることが実感として読み取れるはずである。
【参考】使用しているExcel関数
CONCAT関数、PV関数、ROW関数
解説
以下の論点は、正味現在価値法（NPV法: Net Present Value Method）に共通であるため、「正味現在価値法（NPV法: Net Present Value Method）- 不定額回収」にて説明を付している。
- IRR（内部収益率）との使い分けについて
- NPV法を用いるメリット
- NPV法を用いるデメリット
定額回収の妥当性について
定額回収の前提条件を付すると、年金現価係数という複雑な数字を用いてNPVを計算することになるが、その一方で、不定額回収より計算の手間が省けるので便利でもある。
しかし、実際には、この「定額回収」という条件付けは実務的にはかなり無理がある。例えば、
- 追加投資によるCOFを考慮することができない
- 減価償却費のタックスシールドが投資期間において同額であるという仮説に基づいている
- 終期に廃棄または売却する資産の残存価値や処分損を考慮することができない
- 運転資本の追加投資は初期投資に含めることができるが、終期以降の回収額を反映できない
などといった非現実的な仮定を置く必要がある。
逆に言うと、投資期間が5～15年程度で、回収サイクルが年単位ならば、不定額回収のプロジェクトとして割り切って、減価係数を使用して各期の不定額回収額の現在価値を集計した方がよさそうである。
本稿で紹介した定額回収のパターンを用いるのは、
❶本当に定額回収であるプロジェクト（投資案件）である
❷定額回収の仮定をおいても年差があまり気にならない超長期のプロジェクト（投資案件）※ である
といったケースに限られるのかもしれない。
※ ここでの「超長期」の定義は、年数で何年以上という考え方ではなく、回収時点の数の多さが、処理に困るほどという意味である。月単位で投資回収や積立てが行われる場合は、回収期間が12倍（年×月数）に膨れ上がるからである。その場合には、割引率は、年利ではなく、月利換算するなど、他の引数の処理が手間ではある
投資意思決定（Investment Decisions）の全体像
コメント