- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算手法
概要
正味現在価値法（NPV: Net Present Value Method）は、投資案件やプロジェクトからの全てのキャッシュ・イン・フローとキャッシュ・アウト・フローを割引率を用いて現在価値に置き換えた合計値で投資案件やプロジェクト全体の採算を評価する手法である。
通常、割引現在価値を求める際に使用される割引率には、その企業（投資主体）が直面する市場から見あえりとして得ることが期待できる収益率（期待収益率 RRR: Required Rate of Return）を用いる。
期待収益率の考え方として代表的なものは、
❶ その企業が同程度のリスクを持つ他投資から得られると期待できる収益率（expect to receive in the market）
❷ その企業が投下する経営資源から最低限稼がないといけない期待収益率（minimum rate of return）
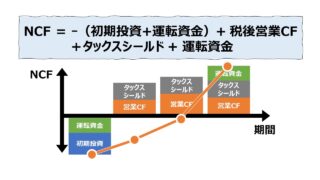
毎期の投資回収額は、会計的利益ではなく NCF（ネットキャッシュフロー）を基本とする。
毎期の回収額が定期定額ではなく、毎期異なる場合や時にはマイナス値（追加投資の必要性やその期の収入が極端に落ち込むなど）になる期を含む場合は、現在価値に置き換えるための簡単な係数法を使うことができない。
そのため、毎期のNCFをそれぞれ算出した後、ひとつひとつのNCFを発生した期間でそれぞれ割引現在価値に置きなおしてから投資案件（プロジェクト）単位で集計することで、投資案件（プロジェクト）全体の割引現在価値を算出する。
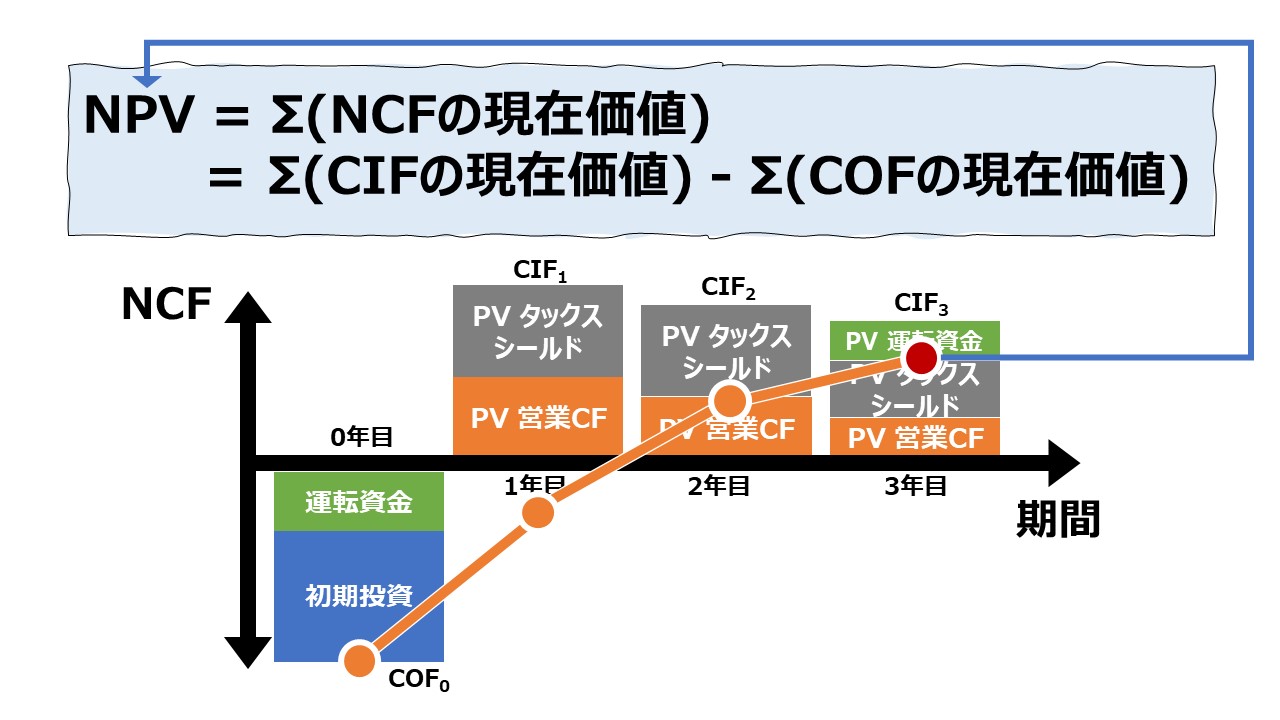
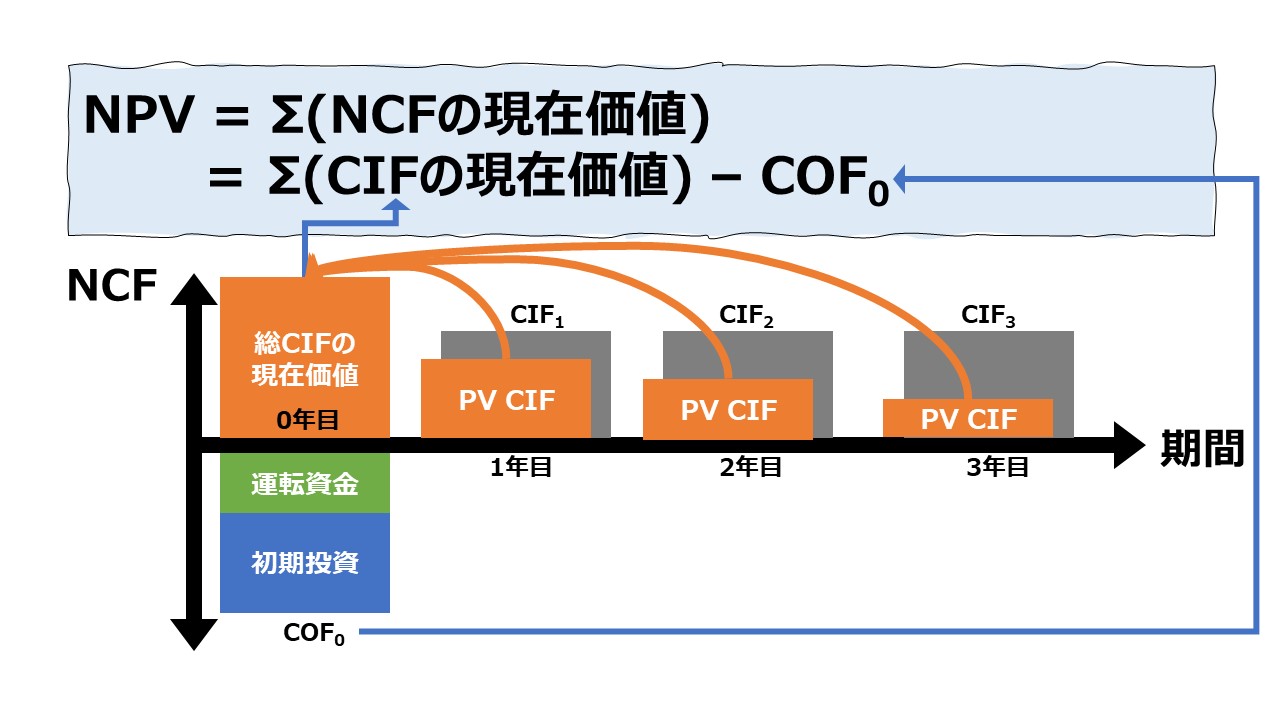
その合計値であるNPVは、投資案件（プロジェクト）全体のキャッシュ・アウト・フロー（COF）とキャッシュ・イン・フロー（CIF）の割引現在価値の合計であるから、
\( \displaystyle \bf NPV＝ CIFの現在価値 – COFの現在価値\)
理解しやすいように、COFは初期投資額のみで、プロジェクト期間中（投資継続中）は各期末にCIFがある典型例で考えると、
添字を用いて、1年目、２年目、３年目・・・を表すのに、n年目、プロジェクト期間を数列としての総和（Σ）で表し、初期投資額は、「-CF0」と捉えれば、
\( \displaystyle \bf NPV＝\sum_{n=1}^N \frac{CF_{n}}{(1+r)^n} -CF_{0}\)
どうしても、数学の記号が理解を妨げる場合は、下記の超シンプル例で数式を頭に浸み込ませればよいかもしれない。
例
初期投資額：100
1年目の収入：55
2年目の収入：60.5
割引率：10%
\( \displaystyle \bf NPV＝\sum_{n=1}^2 \frac{CF_{n}}{(1+0.1)^n} -100\)
\( \displaystyle \bf NPV＝\frac{CF_{1}}{(1+0.1)^1} + \frac{CF_{2}}{(1+0.1)^2 } -100\)
\( \displaystyle \bf NPV＝\frac{55}{(1.1)} + \frac{60.5}{(1.1)^2 } -100\)
\( \displaystyle \bf NPV＝50 + 50 -100\)
\( \displaystyle \bf NPV＝0 \)
今現在、手元にある 100 を投資して、1年後に 55 、2年後に 60.5 を得られるプロジェクトのNPVは、割引率 10% の世界では、ちょうど 0 となる。
つまり、「このプロジェクトに投資してもしなくても、儲けも損もありませんよ」という状態を表す。
確かに、1年後に55、2年後に60.5の合計 110.5 > 100 が得られるプロジェクトは何か得するように感じられるが、割引率10%の作用により、この 100 の投資用資金を他の平均的な投資機会に投下しても、2年後に累計で110.5だけの投資回収が見込めるため、相対的に、このプロジェクトが特別有利なわけではない、ということを、NPVの数字は教えてくれている。
Excel の NPV関数を用いて計算する
とにかく、計算ロジック（理屈）はややこしいから、手っ取り早く結果だけほしい人には、おあつらえ向きに、その名もズバリ「NPV関数」が用意されている。
そして、機械的に数字を当てはめても期待通りの結果が得られない可能性も高い。
NPV関数の使い方はシンプルである。上記と同じ例を用いれば、次のように記述することができる。
=NPV(割引率,値 1,[値 2],…)
初期投資額をNPV関数の外から引いてやると、
=NPV(0.1,55,60.5)-100 = 0 →意図通りに計算された
そのまま機械的にNPV関数を（おそらくは意図に反して）使ってしまうと、
\( \displaystyle \bf NPV(0.1,-100,55,60.5) = -1.29129E-14 \)
\( \displaystyle \bf NPV(0.1,-100,55,60.5) = -1.29129^{\frac{1}{100000000000000}} \)
わずかながら、NPVがマイナスを示す。その認識の差が発生する理由は下図のとおり。
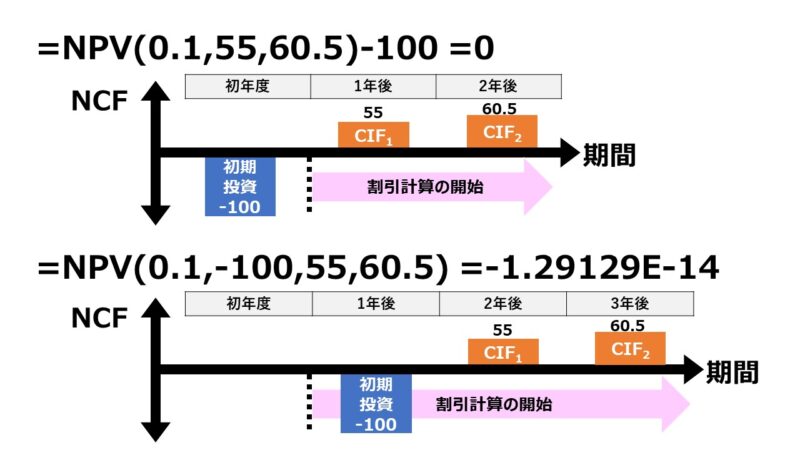
NPV関数は、割引計算対象期間に発生するキャッシュフロー全体の正味現在価値を計算してくれるものだが、マイクロソフト社のバグではなく、ユーザ側がきちんと初期投資額が0期として1期首発生か、それともそのまま1期末発生かを理解し、関数の適用の仕方を使い分けるだけのことである。
ちなみに、これくらいのNPV計算ならば、スプレッド機能の上にマニュアルで割引計算した方が、割引計算の汎用性も失うことなく、その後のグラフ表示の元ネタにも流用できることからおススメである。
なぜなら、割引計算は、
\( \displaystyle \bf 特定期間のNPV= \frac{CF_{n}}{(1+割引率)^n}\)
で求められることが分かっているから、
\( \displaystyle \bf 初期投資のNPV= \frac{CF_{0}}{(1+割引率)^0}\)
\( \displaystyle \bf 初期投資のNPV= \frac{CF_{0}}{1} = CF_{0} \)
となるだけだからである。
（底の数（1+割引率の値）が何になっても、ゼロ乗は全て１になる）
その他の資本予算の構成について
☞NCFの意味を確認するには、下記稿を参考にするとよい。
☞各期の抽出すべき取引内容を確認するには、下記稿を参考にするとよい。
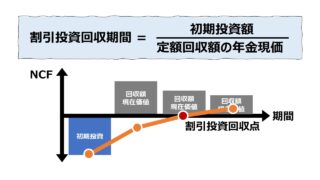
☞割引現在価値を求めるための、❶年利、❷回収期間、❸回収額の関係を知るためには、下記稿を参考にするとよい。
計算プロセス
定額回収による正味現在価値法（NPV法）の計算プロセスは、基本的に、「割引回収期間法（定期定額回収）」と同じで、投資案件（プロジェクト）の投資採算の評価基準として「割引回収期間」という時間軸を用いたものか、それとも実現が期待できる正味収益の絶対額を用いたものかという違いになる。
- 初期投資額の計算初期投資額を明らかにする
・設備投資などの初期投資額
・追加で必要になる運転資金 など - 回収NCFの計算各期ごとの回収NCFを計算する
・各期のCIFとCOFを相殺した正味（ネット）額を計算する
・税引後で計算する - 割引率の設定投資回収額を現在価値に置き換えるための割引率を設定する
・各期の投資回収額を現在価値に割り引くための予定利率を想定する
・年利で求めれば回収期間の単位は年になる - 割引後NCFの計算各期のNCFの割引現在価値を求める
・現在価値の考え方に基づき、各期の回収額と割引率の組み合わせで決まる現価係数を用いて、割引回収額を計算する
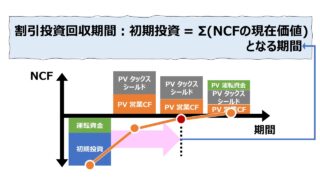
- NPVの算出各期のNCFの割引現在価値（NPV）の合計を求める
・NPV＝1年目のNCFの現在割引価＋・・・＋最終年のNCFの現在割引価値
- 投資採算性の判断NPVの正負の大きさで、投資収益性を判定する
・NPV＞０ならば、投資額を上回る価値を創出していると判断できる
NPVの計算自体は、Excel関数も存在することから、Excel関数を意図に反して使ってしまう（初年度の初期投資額を割引計算対象に入れるか入れないか）ことだけ注意しておけば、大した手間もかからずあっけないぐらい簡単に計算することができる。
大事なことは、そのNPV計算にかけるべき各期のNCFの洗い出しの方であり、かかる手間暇もほぼこれが99%を占めるものと思われる。
シミュレーション
Excelテンプレート形式で各期不定額の投資回収が見込める場合の正味現在価値（NPV）を求める計算方法を示す。
入力欄の青字になっている「期間（任意の期間名）」「初期投資額」「追加投資額」「運転資金投資」 「運転資金投資回収」 「追加運転資金投資」 「追加運転資金投資回収」 「営業CF」「減価償却費」 「設備の売却/廃棄にかかる現金収入」「設備の未償却残高（簿価）」「設備の売却/廃棄にかかる現金支出」「設備の売却/廃棄にかかる税率」「営業CFにかかる税率」「割引率」に任意の数字を入力すると、5期からなる資本予算に基づく正味現在価値（NPV）が求められる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
グラフの見方
Excelの折れ線グラフを用いてグラフ表示している。
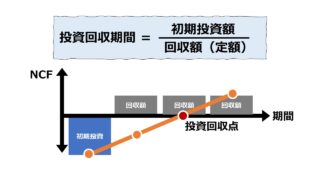
横軸は経過年を示しており、0.0年（ゼロ年）が初期投資した時点で、縦軸の金額がちょうどゼロになったときが、初期投資額を回収した時点ということになる。
ここまでは、投資回収期間（または割引投資回収期間）を表すグラフと同じである。
違いは、投資回収期間法では、開始年（初期投資タイミング）から、投資回収がなされた期間までが描画されれば事足りるところが、NPVは全プロジェクト期間（全投資期間）にわたって計算・描画される必要がある点。
よって、Excelテンプレートを用いてグラフ表示をきちんとしたい場合は、評価対象となるプロジェクト（投資案件）の終期まできちんと確保されたものにしてから使用を開始する必要がある。
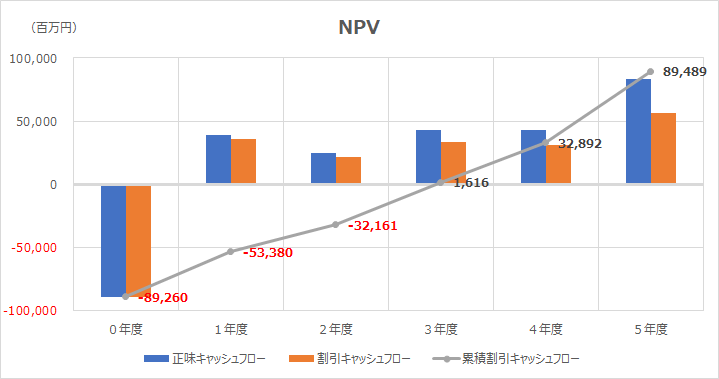
テンプレートで用いた例では、3年目にして漸く利益がプラスに転じ、5年目には単期で 56,597、累計で 89,489 の割引正味キャッシュフローとなっている。
各期のキャッシュフローは、割引前と割引前をあえて並べて表記している。その差は、投資開始時期から離れれば離れるほど、大きくなっていることが分かる。
時間が長ければ、割引率（裏返すと時間の利益、金利みたいなもの）の効果が大きくなることが実感として読み取れるはずである。
【参考】使用しているExcel関数
NPV関数、SUM関数
解説
IRR（内部収益率）との使い分けについて
共通の計算構造について
共に、割引現在価値をベースにプロジェクト（投資案件）の投資採算評価技法として有名なIRR（内部収益率：Internal Rate of Return）との相違をここでは見ることで、NPVへの理解を深めることにする。
NPVとIRRの基本の計算構造は、裏表の関係にあるため、一方の指標に対する理解を深めると、もう一方への理解も深まる傾向が高い。
先述のシンプル例を再掲する。
例
初期投資額：100
1年目の収入：55
2年目の収入：60.5
割引率：10%
ここに、0年度は、割引率計算においては、0乗だという数学知識を加えてやると、
\( \displaystyle \bf NPV＝ \frac{CF_{0}}{(1+0.1)^0} + \frac{CF_{1}}{(1+0.1)^1} + \frac{CF_{2}}{(1+0.1)^2 }\)
\( \displaystyle \bf NPV＝ \frac{-100}{1.1^0} + \frac{55}{1.1^1} + \frac{60.5}{1.1^2 }\)
\( \displaystyle \bf NPV＝-100+50 + 50 = 0\)
逆に、NPV がゼロになる割引率を r と置いた場合、上式は、
\( \displaystyle \bf NPV＝ \frac{CF_{0}}{(1+r)^0} + \frac{CF_{1}}{(1+r)^1} + \frac{CF_{2}}{(1+r)^2 }=0 \)
\( \displaystyle \bf NPV＝ \frac{-100}{(1+r)^0} + \frac{55}{(1+r)^1} + \frac{60.5}{(1+r)^2 }=0 \)
と表現でき、これを 割引率：r で解くと、r=10%（0.1）となる。
すなわち、割引現在価値（PV）の計算という関数を用いて、
❶各期のNCF、❷割引率が分かれば、NPV を計算することができ、
❶各期のNCF が分かり、❸NPV=0 という前提が置かれると、IRRを計算することができる。
ちなみに、詳細はIRRの解説ページに譲るが、NPVが計算できたとしても、IRRは計算できない場合（解が無し）もあるし、解が2つ以上存在する場合もある。
NPVとIRRの使いどころ
前章で触れた通り、IRRは解が無かったり、２つ以上解を持ったりしてしまうので、時には取り扱いに困ることがある。
それゆえ、会計実務において、NPVかIRRかどちらを使えばよいか迷う場合は、迷いを断ち切り、NPVを用いることが早道であることが圧倒的に多い。
NPVで投資採算を評価したい場合とは、前提となる割引率が分かっていて、同じ割引率を適用して、複数の投資プランを対比させるとか、ひとつのプランに投資するか中止するかの判断をするためにNPVを使いたいからである。
逆に、割引率データを入手できずに、とりあえず企業（自身）が置かれている状況下で、適切な期待収益率の前提が全く分からない場合に、分析対象とするプロジェクト（投資案件）のNPVをゼロにする損益トントンの割引率をいったん知りたい、という場合にIRRを算出することが多いからである。
よく勉強されている方の中には、ハードルレートと分析対象のプロジェクトのIRRを比較して、ハードルレートを上回ったプロジェクトの実行を決断するのにIRRを使用することを知っている方がいらっしゃるかもしれない。
残念ながら、その適用方法は半分正解で半分間違っている可能性が高い。
ハードルレートを超えるIRRを持つプロジェクトは、ハードルレートを割引率に用いてNPVを計算し、NPVが正になったり、NPVがより大きい方を採用しても、大きく判断を間違えることはあまりない。
しかし、特に資本予算制約のある中で、IRRを基準にプロジェクトの取捨選択を行うと、投資ポートフォリオ全体の収益性がかえって低くなる可能性が高い。
IRRの計算構造の中に、IRRが高くてもNPVが小さくなるもの（厳密にはNPVのリターン率、BCR、NPV-Rなどと呼ばれる指標）が発生することが不可避となる要因が含まれているからである。
- NPVは割引率が分かっていないと計算できないし、IRRはNPV=0になる割引率を求めるもの
- それでもどちらを使うか迷うときは、NPVを使った方が間違いが少ない
- それに加えて、IRRは「解なし」「解が2つ以上」という結果になることも多い
NPV法を用いるメリット
NPVは、プロジェクトプロファイル情報に加え、割引率の情報を必要とするが、その手間と複雑性を上回るメリットがあると考えられている。
NPV法を用いるデメリット
NPVは有用性の高い計算方法であるという風評が最初になるおかげで、要らぬ期待値まで高まってしまい、計算結果と算出手順の複雑さから、かえって「使えない技法」というレッテルを張られることも多い。
これは、割引率を用いる評価技法に共通するデメリットだということもできる。
「量」と「質」の問題というのは社会・経済の中に結構内在している。
NPVの大きいプロジェクトはその分、巨額の投資額を必要とする可能性も高いので、一律、NPVの大きいものを優先して投資することが全体の収益性を高めるとまでは言えない。
プロジェクト投資の採算性を見極めるのは、もう少し知恵※が必要となる。
（※もちろん、本テーマを全て読了いただければ、その知恵を育むことができると信じて原稿を作成している）
投資意思決定（Investment Decisions）の全体像
コメント