- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算手法
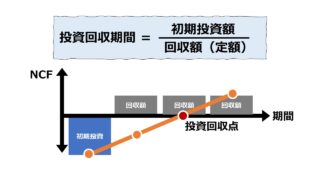
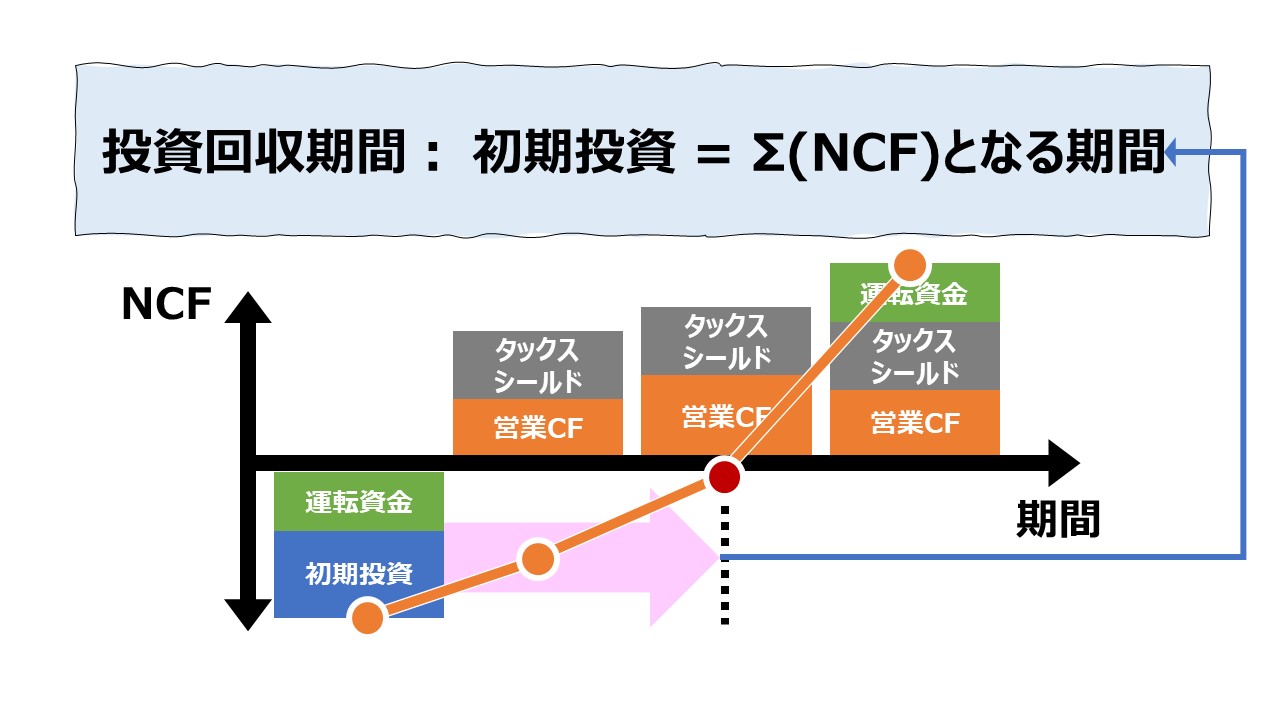
回収期間法（Payback Period, Payback Method）は、初期投資額が全額回収されるまでにどれくらいの期間（の長さ）が必要かを測定することで、投資の回収安全性の観点から投資可否判断をするためのツールである。
投資の回収安全性の観点からは、できるだけ回収期間が短い方が好まれる。
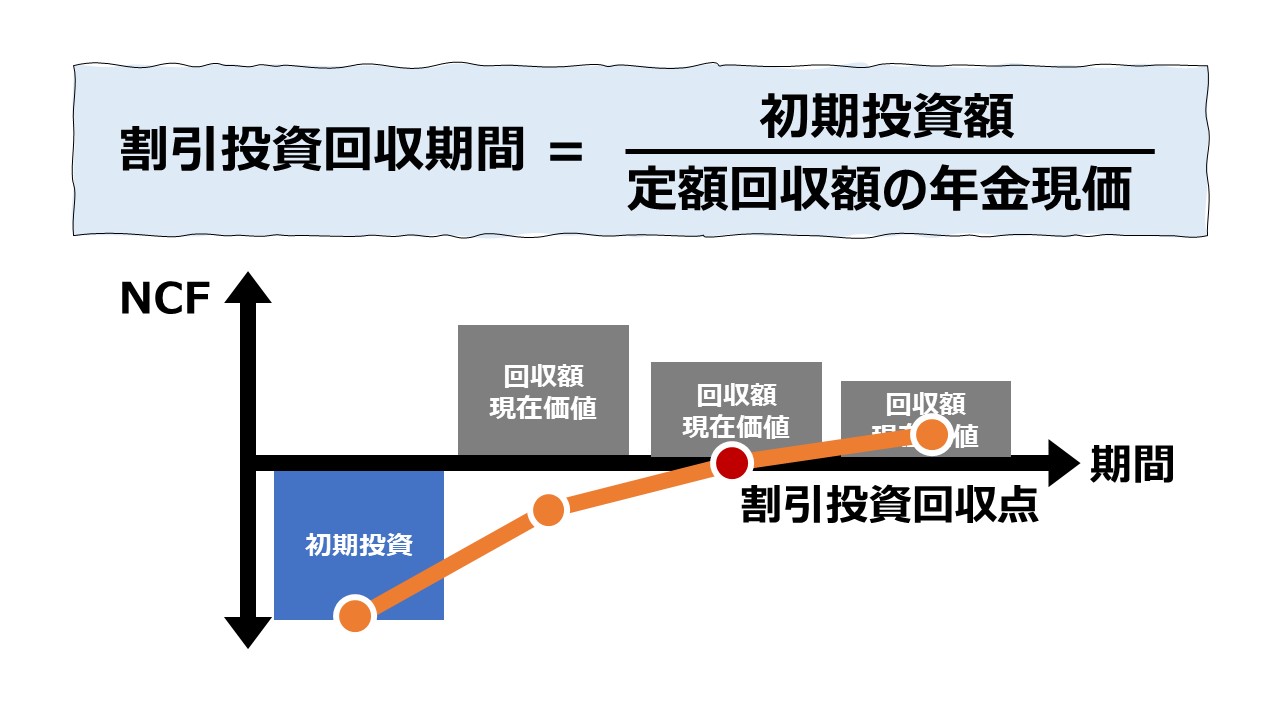
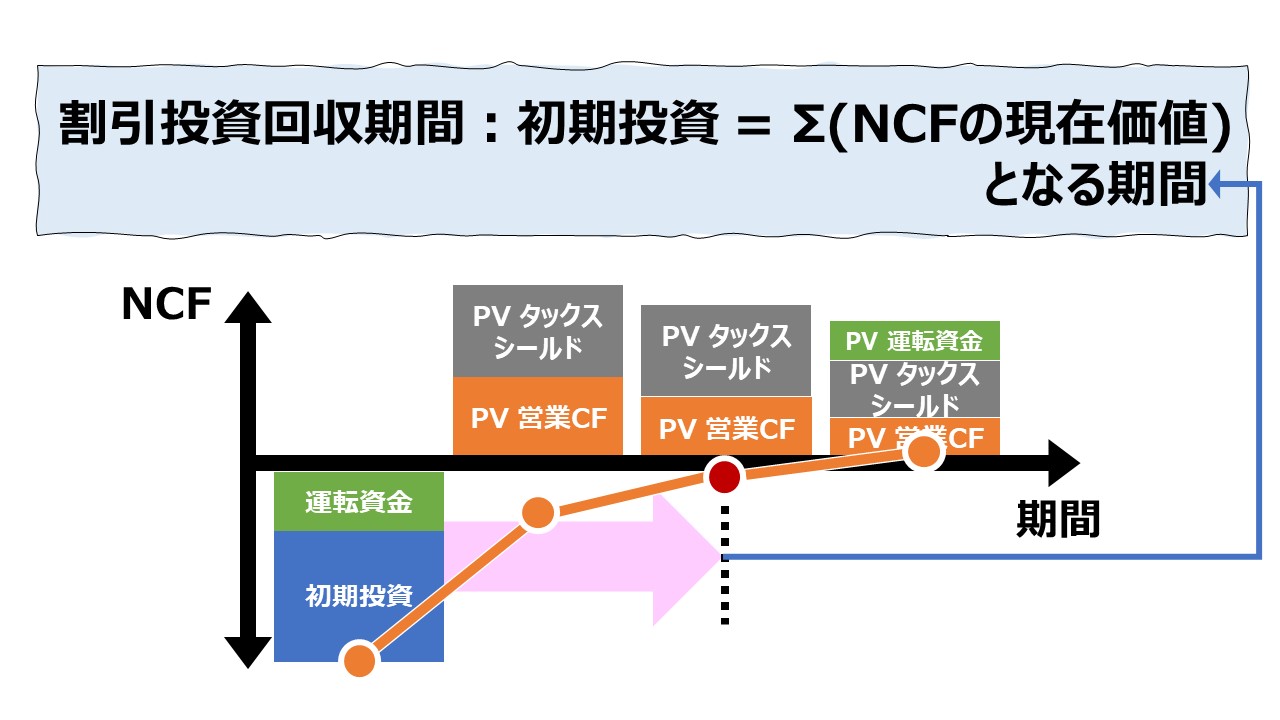
割引回収期間法（Discounted Payback Period, Discounted Payback Method, Breakeven Time）は、回収期間法において、毎期の回収額を現在価値に置き換えたものを用いて回収期間を計算する技法である。
こうすることで、従来の回収期間法の特徴に加えて、「お金の時間価値」を考慮したうえで投資回収期間を算定することが可能になる。
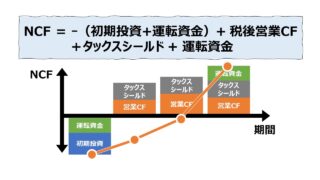
毎期の投資回収額は、NCF（ネットキャッシュフロー）として計算されることになる。
投資の回収条件として、
❶毎期必ず定期的に投資回収がなされる
❷それぞれの回収額は一定（不変）である
という条件が付された場合、非常にシンプルな計算式で、割引投資回収期間を求めることができる。
\( \displaystyle \bf 割引投資回収期間（年）＝ \frac{初期投資額}{定期定額NCFの年金現価}\)
「年金現価」とは、「将来支払われる年金総額を現在価値に割引計算した額」である。
計算方法は、毎年発生する年金額（この場合は定期定額の投資回収額を意味する）を予定利率（割引率）により現在時点まで割引計算したものを合計する。
なぜ、「毎期一定額」という条件がシンプルな計算式を導くカギを握るかというと、年金現価を計算するとき、年金額が一定であるなら、年金額に「年金現価係数」なる数字を掛け算してあげるだけで、年金現価を計算することが可能だからである。
\( \displaystyle \bf 年金現価 ＝ 年金額 \times 年金現価係数 \)
例えば、年金額（毎期の投資回収額）が14,237円で、投資回収期間が10年間で、予定利率が 7% だとしたら、年金現価係数は 7.024 と予め分かっている（※）ので、
\( \displaystyle \bf 年金現価 ＝ 14,237円 \times 7.024 \)
\( \displaystyle \bf 年金現価 ≒ 100,000円 \)
となる。
（※）「予め分かっている」の意味は、割引率と回収期間の組み合わせで年金現価係数が計算できるということ。実際に探し求める具体的方法は「解説」箇所で説明
この計算式を逆に解釈していくと、最初に投資した100,000円に対して、毎年 14,237円ずつ回収することができたなら、予定利率が7%の場合は、ちょうど10年間で回収可能である、と考えることができるわけである。
計算プロセス
前章で解説した通り、毎期一定額の回収のケースは非常にシンプルな手順で割引投資回収期間を求めることができる。
- 初期投資額の計算初期投資額を明らかにする
・設備投資などの初期投資額
・追加で必要になる運転資金 など - 回収NCFの計算各期の定額回収NCFを計算する
・各期のCIFとCOFを相殺した正味（ネット）額を計算する
・税引後で計算する
・現実的に一定額でない場合、概算になるが平均値も使える - 割引率の設定投資回収額を現在価値に置き換えるための割引率を設定する
・各期の投資回収額をまとめて現在価値に割り引くための予定利率を想定する
・年利で求めれば回収期間の単位は年になる - 割引回収期間の計算初期投資額、定額回収額、割引率から割引投資回収期間を計算する
・「年金現価」の考え方に基づき、定期回収額（年金額）と割引率の組み合わせで決まる年金現価係数を用いて、初期投資額に一致する期間を求める。
シミュレーション
Excelテンプレート形式で各期定額の投資回収が見込める場合の割引投資回収期間を求める計算方法を示す。
入力欄の青字になっている「初期投資額」「定期回収額」「割引率（予定利率）」が必須入力項目となっている。
割引投資回収期間を求めるためにExcel関数の中から NPER関数 を採用しているが、引数として、任意入力項目である「将来価値」「回収期日フラグ」の2つは原則として使用しない。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
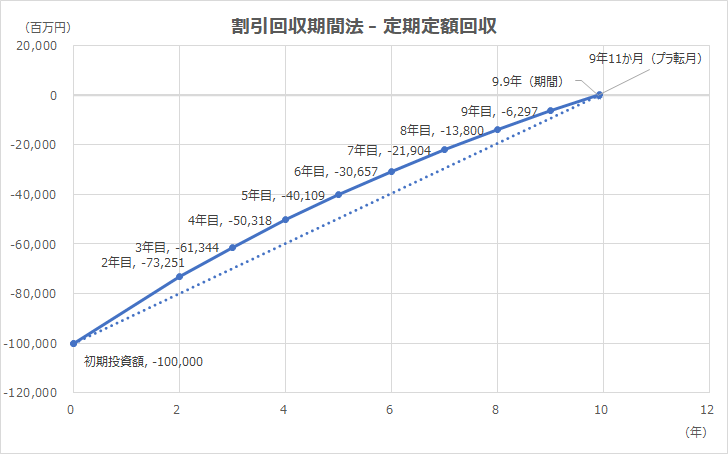
グラフの見方
Excelの散布図を用いてグラフを表示している。
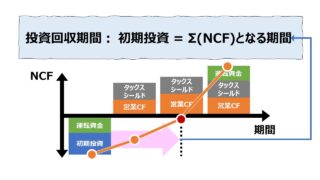
横軸は経過年を示しており、0.0年（ゼロ年）が初期投資した時点で、縦軸の金額がちょうどゼロになったときが、初期投資額を回収した時点ということになる。
初期投資は、キャッシュフローのベクトル方向から、マイナス値を用いて表現し、各期の回収されるべきNCFはプラス値を想定して作成している。
（そもそもNCFがマイナスの場合、何年かかっても初期投資額は回収できない）
投資回収線がy軸上でゼロになる点のx座標が投資回収期間（年）であり、小数点有りで表示されている。
小数点部分を月表示に変換し月中の場合は月末になるように調整してある（→プラ転月）。
VBAマクロ/ソルバー等を使用しないという制限から、投資回収期間内の「X年目」は、最大8年分のみ用意してある。投資回収期間の伸び縮みで自動的に刻み年が調整される。
通常は、初期投資年度から割引投資回収年度までの間、上に凸の折れ線グラフになるはずである。
参考として、初期投資年度から割引投資回収年度まで直線も引いているが、これは、割引をしない場合の投資回収期間線を示すものではない。
→ ∵ 割引をしない投資回収期間線は、x軸との交点がそもそも割引投資回収期間線とは異なる
CONCAT関数、MOD関数、NPER関数、PV関数、ROUNDDOWN関数、ROUNDUP関数
解説
「年金現価係数」の求め方
「年金現価係数」 を使う必要性まで理解できたと仮定して、次はどうやって「年金現価係数」なる数字をはじき出すかが問題となる。
従来は、利率と運用期間（投資回収期間）のクロステーブルである「年金現価係数表」から条件に当てはまる年金現価係数を探してきて、毎年の年金額（回収額）に掛け算していた。
最近では、Excelなどの表計算ソフトに専用の関数も準備されているし、計算式自体を知っていれば、スプレッドシート上で計算式を簡単に自分でも組むことができる。
\( \displaystyle \bf 年金現価係数 ＝ \frac{(1+i)^n-1}{i(1+i)^n} \)
\( i=割引率(予定利率), n=年数 \)
前述の、7% で10年間 を当てはめると、
\( \displaystyle \bf 年金現価係数 ＝ \frac{(1+0.05)^{10}-1}{0.05(1+0.05)^{10}} \)
\( \displaystyle \bf 年金現価係数 ＝ \frac{(1.05)^{10}-1}{0.05(1.05)^{10}} \)
\( \displaystyle \bf 年金現価係数 ＝ \frac{1.62889-1}{0.05 \times 1.62889} \)
\( \displaystyle \bf 年金現価係数 ＝ 0.62889 \div 0.08144 \)
\( \displaystyle \bf 年金現価係数 ＝ 7.72173… ≒ 7.721 \)
Excelの場合は、PV関数を使用することになる。
= PV(利率, 期間数, 支払額, [将来価値], [支払期日])
引数が5つもあるが、
- 利率：投資回収に用いる割引率
- 期間数：投資回収期間
- 支払額：この場合は回収額（年金額）
- [将来価値]：この場合は「0（ゼロ）」固定
- [支払期日]：期末に回収ならば「0（ゼロ）」固定
というわけなので、実質的には、割引率と回収期間と投資回収額の3つが分かればよい。
表計算ソフトがまだ登場する前、どうやって計算を手早く済ますか天才的な式を編み出した先人の叡智に表敬して、式の意味が分からずとも、我々は上式を使うだけでまずは目的を果たそう。
NPER関数
❶割引率、❷投資回収期間、❸投資回収額の３つから年金現価係数をはじき出す方法について、年金現価の理解のために、PV関数 の成り立ちを説明したに過ぎない。
残念ながら、本稿における投資回収期間そのものを PV関数 は教えてくれない。なぜなら、PV関数の引数の内、 ❷投資回収期間 が本稿で求めたい割引投資回収期間そのものだからである。
直接、❶割引率、❷投資回収額、❸初期投資額 の組み合わせから、割引投資回収期間を導き出してくれるのが、Excelにおける NPER関数 である。
= NPER(利率, 定期支払額, 現在価値, [将来価値], [支払期日])
引数が5つもあるが、
- 利率：投資回収に用いる割引率
- 定期支払額：この場合は回収額（年金額）
- 現在価値：この場合は初期投資額（マイナス値で入力する）
- [将来価値]：この場合は「0（ゼロ）」固定
- [支払期日]：期末に回収ならば「0（ゼロ）」固定
というわけなので、実質的には、割引率と投資回収額と初期投資額の3つが分かればよい。
回収期間法を用いるメリット
回収期間法はただでさえ簡単で分かりやすいうえに、定期定額の回収という条件が付けたされると、2つの数の割り算だけで求めることができるため、その分かりやすさに拍車がかかる。
回収期間法を用いるデメリット
回収期間法は簡単で分かりやすいということは、その分だけ捨てたものも多くなるため、以下のようなデメリットを内包していることに留意する必要がある。
投資意思決定（Investment Decisions）の全体像
コメント