- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算手法
概要
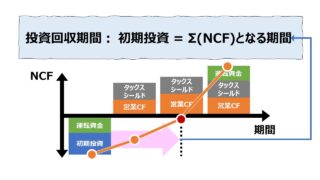
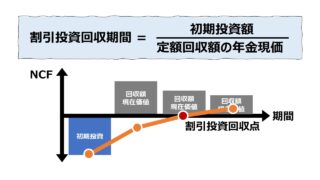
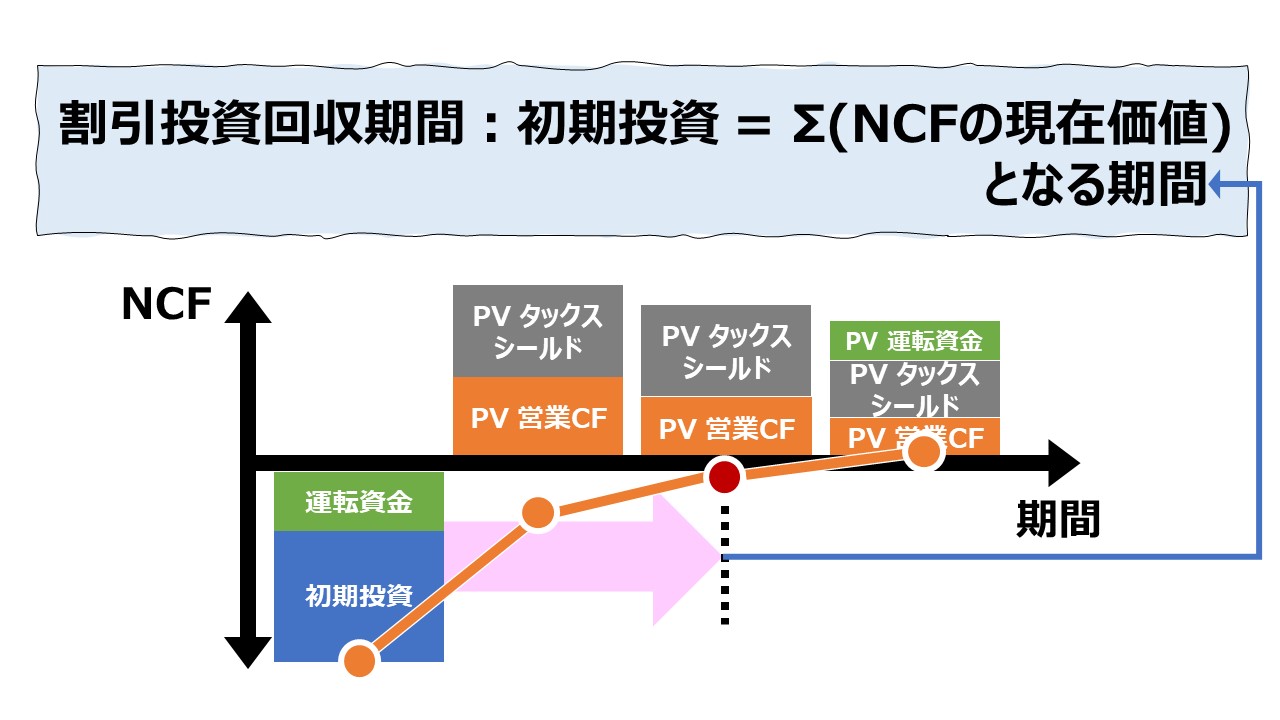
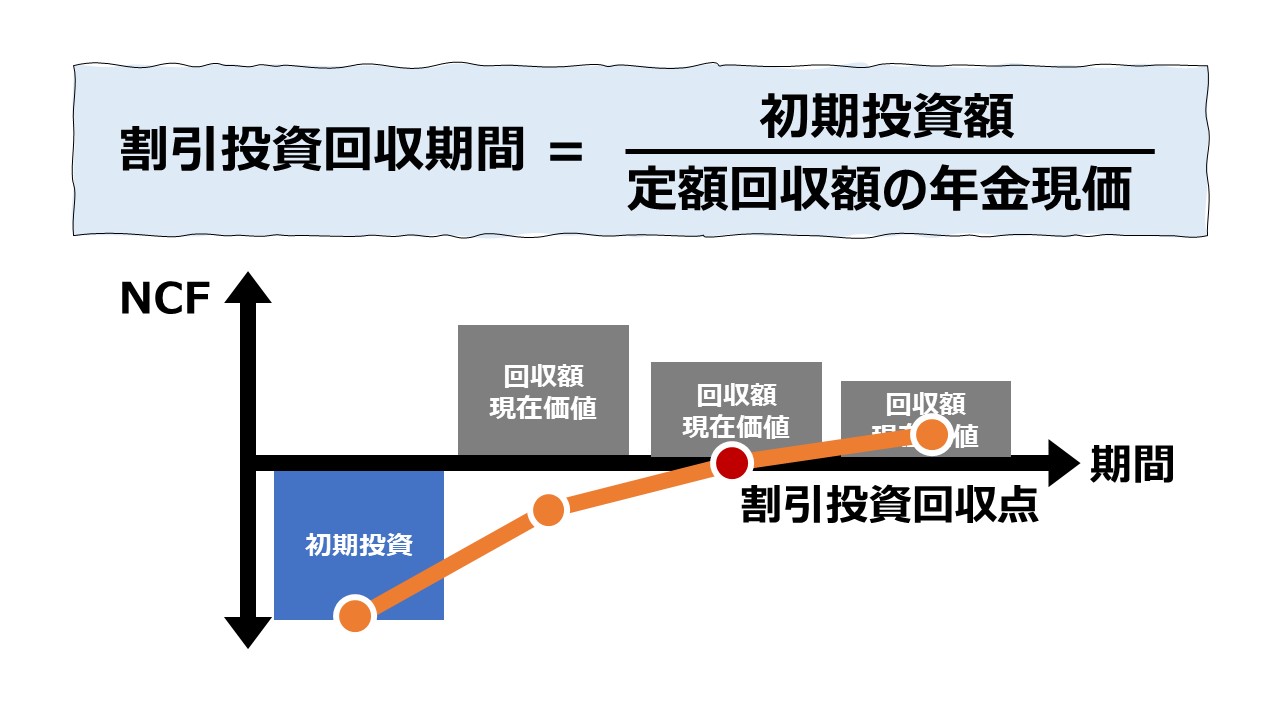
割引回収期間法（Discounted Payback Period, Discounted Payback Method, Breakeven Time）は、現在価値に置き換えた毎期の回収額を合計していって、初期投資額が回収される期間を計算する技法である。
投資回収期間が短ければ短いほど高く評価されるため、投資回収の安全性の観点から投資可否判断をするためのツールとして利用される。
従来の回収期間法の特徴に加えて、回収額を全て現在価値に置き換えることで「お金の時間価値」の考慮後の金額ベースで投資回収期間を算定することが可能になる。
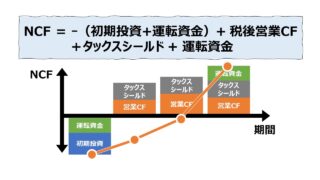
毎期の投資回収額は、会計的利益ではなく NCF（ネットキャッシュフロー）を基本とする。
毎期の回収額が定期定額ではなく、毎期異なる場合や時にはマイナス値（追加投資の必要性やその期の収入が極端に落ち込むなど）になる期を含む場合は、現在価値に置き換えるための簡単な係数法を使うことができない。
そのため、毎期のNCFをそれぞれ算出した後、ひとつひとつのNCFを発生した期間でそれぞれ割引現在価値に置きなおしてから合計することになる。
毎期の割引後累積NCFがちょうどゼロになる時点が、割引投資回収期間ということになる。
この計算方法を言葉と式で表すと次のようになる。
\( \displaystyle \bf 割引投資回収期間（年）＝ 割引累計NCFがマイナスである年数 – \frac{最後のマイナス割引累計NCF額}{プラ転する期の割引NCF額}\)
これは無理やり数式を使うと却って理解を妨げることになる好例のひとつだが、投資回収期間をまず２つの部分に分けることから始める。
- まるまる１年(Full year)が投資回収に必要な年数
- こういう年は、その年までの割引累計NCFはまだマイナスのまま沈んでいるはずである
- 期の途中で累計NCFがマイナスからプラスに変わった年において、実際にプラスに変わった月数
- 年初に残っているマイナス割引累計NCFをその年で回収可能な割引NCFで割り算して月数を算出
上記のような月数計算が成り立つためには、２つの仮定を置いている。
❶月次で投資回収が行われている
❷月末に投資回収が行われている
ちなみに、右辺第2項の符号がマイナスになっているのは、割り算の分子がマイナス値で分母がプラス値になるためである。結果として、正数となって Full year（1年）の年数に月数として足されていく。
厳密な計算のことを言えば、割引計算は複利計算なので、極端な話、日別や時間別にでも複利計算が可能になり、当然に期間が異なれば複利計算結果も異なる。
上式は、年単位の複利計算で割引価値を求め、年に足らない月単位は、ざっと単利で月数計算をしている。
年単位未満の複利計算を考慮した方法は別途解説する予定である。
☞NCFの意味を確認するには、下記稿を参考にするとよい。
☞各期の抽出すべき取引内容を確認するには、下記稿を参考にするとよい。
☞割引現在価値を求めるための、❶年利、❷回収期間、❸回収額の関係を知るためには、下記稿を参考にするとよい。
割引現在価値の計算
回収額の割引現在価値は、回収額に予め分かっている「現価係数」を乗じるだけで算出できる。
例えば、5年間で7%の組み合わせにおける「現価係数」は .713 なので、5年後に回収される 100万円の現時点の価値は、
割引現在価値 = 100万円 × 0.713 = 71.3万円
となる。
これは、現在もしも手許に 71.3万円あって、5年間かけて、複利（利息にも孫利息が付く）で7% の運用ができたとしたら、100万円 になる元本利息計算を時計を逆回しに5年後から現在を見たものに置き換えた計算である。
「現価係数」の求め方・考え方は「解説」の章を参照。
計算プロセス
割引投資回収期間の計算（不定額回収）プロセスは、基本的に「回収期間法（不定額回収）」の手順に、「割引回収期間法（定期定額回収）」で説明した割引現在価値計算を加えたものになる。
- 初期投資額の計算初期投資額を明らかにする
・設備投資などの初期投資額
・追加で必要になる運転資金 など - 回収NCFの計算各期の定額回収NCFを計算する
・各期のCIFとCOFを相殺した正味（ネット）額を計算する
・税引後で計算する - 割引率の設定投資回収額を現在価値に置き換えるための割引率を設定する
・各期の投資回収額を現在価値に割り引くための予定利率を想定する
・年利で求めれば回収期間の単位は年になる - 割引後NCFの計算各期のNCFの割引現在価値を求める
・現在価値の考え方に基づき、各期の回収額と割引率の組み合わせで決まる現価係数を用いて、割引回収額を計算する
- 累積割引NCFマイナス期間の特定累積割引NCFがマイナスになっている期間をカウントする
・累積割引NCFがマイナスということは、まだ投資回収中である（回収残がある）
- 残月計算プラ転する年における月数をカウントして加える
・割引累計NCFの最後のマイナス値を翌期の割引回収NCFで割り算して、×12することで月数を求める
念押しだが、プラ転する月数計算には、複利を使用していない（最終年は単利でもってリニアに計算）。
理由は、そこまで厳密に複利計算しても、手間の分を上回る正確性が得られないからである。
シミュレーション
Excelテンプレート形式で各期不定額の投資回収が見込める場合の割引投資回収期間を求める計算方法を示す。
入力欄の青字になっている「期間（任意の期間名）」「初期投資額」「追加投資額」「運転資金投資」 「運転資金投資回収」 「追加運転資金投資」 「追加運転資金投資回収」 「営業CF」「減価償却費」 「設備の売却/廃棄にかかる現金収入」「設備の未償却残高（簿価）」「設備の売却/廃棄にかかる現金支出」「設備の売却/廃棄にかかる税率」「営業CFにかかる税率」「割引率」に任意の数字を入力すると、5期からなる資本予算に基づく割引投資回収期間が求められる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
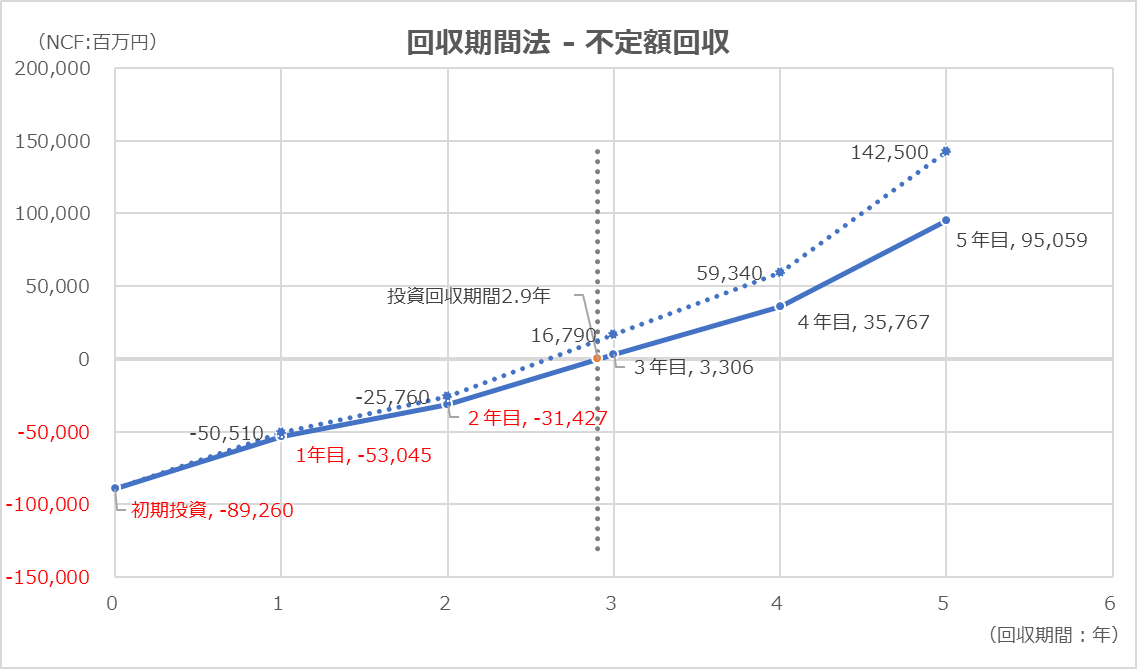
グラフの見方
Excelの散布図を用いてグラフを表示している。
横軸は経過年を示しており、0.0年（ゼロ年）が初期投資した時点で、縦軸の金額がちょうどゼロになったときが、初期投資額を回収した時点ということになる。
初期投資は、キャッシュフローのベクトル方向から、マイナス値を用いて表現し、各期の回収されるべきNCFはプラス値を想定して作成している。
（そもそもNCFがマイナスの場合、何年かかっても初期投資額は回収できない）
投資回収線がy軸上でゼロになる点のx座標が割引投資回収期間（年）であり、小数点有りで表示されている。
参考として、割り引く前の各期NCFの値を点線で示して両者を比較できるようになっている。
通常は、現在価値に割り引かれている分だけ各期のNCFの方が値が大きくなるため、実線より点線の方が上にプロットされているはずである。
それゆえ、割引回収期間は通常の回収期間より長くなっているはずである。
【参考】使用しているExcel関数
CONCAT関数、COUNTIF関数、IF関数、INDEX関数、ROUNDUP関数、SUM関数
解説
「現価係数」の求め方
「現価係数」 を使う必要性までは理解できたと仮定して、次はどうやって「現価係数」なる数字をはじき出すかが問題となる。
従来は、利率と運用期間（投資回収期間）のクロステーブルである「現価係数表」から条件に当てはまる現価係数を探してきて、各年の該当する投資回収額に掛け算していた。
最近では、Excelなどの表計算ソフトに専用の関数も準備されているし、計算式自体を知っていれば、スプレッドシート上で計算式を簡単に自分でも組むことができる。
\( \displaystyle \bf 現価係数 ＝ \frac{1}{(1+i)^n} \)
\( i=割引率(予定利率), n=年数 \)
前述の、7% で5年間 を当てはめると、
\( \displaystyle \bf 現価係数 ＝ \frac{1}{(1+0.07)^5} \)
\( \displaystyle \bf 現価係数 ＝ \frac{1}{1.07^5} \)
\( \displaystyle \bf 現価係数 ＝ \frac{1}{1.40255} \)
\( \displaystyle \bf 現価係数 ＝ 0.712986… ≒ 0.713 \)
Excelの場合は、PV関数を使用することになる。
= PV(利率, 期間数, 支払額, [将来価値], [支払期日])
引数が5つもあるが、
- 利率：投資回収に用いる割引率
- 期間数：投資回収期間
- 支払額：この場合は「0（ゼロ）」固定
- [将来価値]：その期の回収額
- [支払期日]：期末に回収ならば「0（ゼロ）」固定
というわけなので、実質的には、割引率と回収期間とその期の回収額の3つが分かればよい。
表計算ソフトがまだ登場する前、どうやって計算を手早く済ますか天才的な式を編み出した先人の叡智に表敬して、式の意味が分からずとも、我々は上式を使うだけでまずは目的を果たそう。
※なお上記テンプレートでは、PV関数は用いずにべき乗を含む現価係数の計算式をExcel演算子だけで構築している
回収期間法を用いるメリット
回収期間法はややこしい複雑な計算をやらなくて済むので簡単で分かりやすい。割引回収期間法はそれにお金の時間価値の考慮ポイントを付け加えたものになる。
回収期間法を用いるデメリット
回収期間法は簡単で分かりやすいということは、その分だけ捨てたものも多くなるため、以下のようなデメリットを内包していることに留意する必要がある。
デメリットの後2つは、上記テンプレートを眺めているだけでは理解することが難しいだろう。
ごく自然に、本稿で提示しているExcelテンプレートは、5年間で投資回収が終わることが分かっており、解としての割引投資回収期間が5年以内に到来するケースを大前提として使用している。
もし仮に、割引率が思った以上に高く設定されて、5年以内に投資回収が見込めない場合、
（ケース１）投資回収できるまでプロジェクト案件を永遠に延長できる
・Excelテンプレートの投資継続期間を延長して、投資回収できる時点まで試行錯誤的に伸ばしていき、力業で解を見つける
・回収額が未来永劫プラスであっても、割引率が高いために永遠に投資回収点に到達できない可能性がある
（ケース2）投資回収期間をある程度（例：10年程度）には延長できる
・Excelテンプレートの投資継続期間をある程度延長して、投資回収時点を力業で見つける
・回収額の総合計がそれでも初期投資額に未達で、与えらえた延長期間を使い切っても解が得られない可能性がある
という割引投資回収期間が見つけられるかどうかわからない不安定な状態で、計算に挑まなくてはならない。
これは、割引投資回収期間法のみならず、投資回収期間法にも共通する性質である。
こういう解が見つからない不安定さや、割引率を投資案件（プロジェクト）の全体収支を含めて設定するためには、NPV法（正味現在価値法）など、他の手法を使用しなければならない。
投資意思決定（Investment Decisions）の全体像
コメント