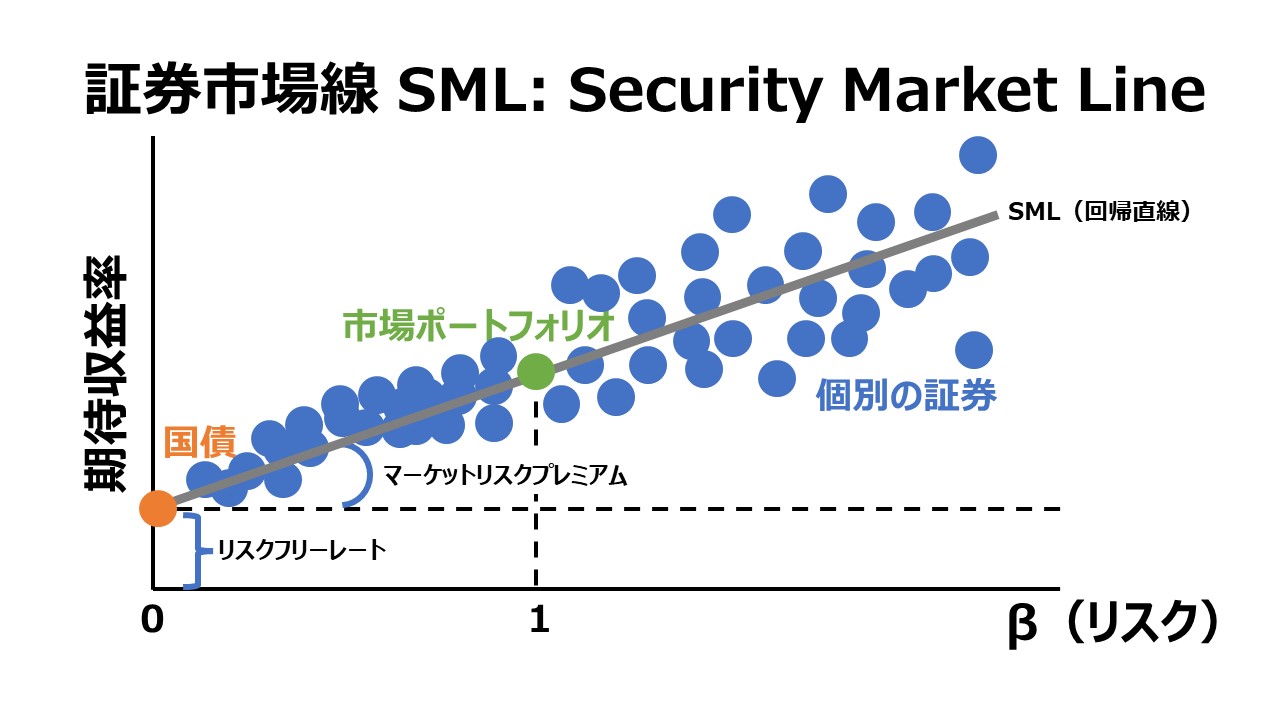
証券市場線 SML: Security Market Line
概要
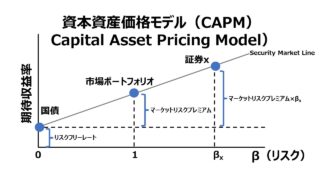
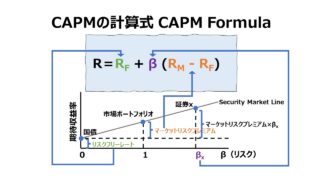
資本資産価格モデル Capital Asset Pricing Model (CAPM)をグラフとして可視化したものが証券市場線(SML: Security Market Line)になる。
株式市場全体の必要収益率(目標収益率)が各β値(システマティック・リスク)水準における個別証券の平均値を示すものだとしたら、縦軸に必要収益率(required rate of return)、横軸にβ値をとったグラフ上では、それは右肩上がりの回帰線を描くことになるだろう。それが証券市場線(SML)の正体である。
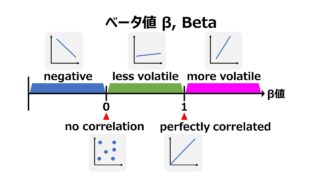
ハイリスクのより大きいβには、ハイリターンの必要収益率がプロットされ、ローリスクのより小さいβには、ローリターンの必要収益率がプロットされることになる。これは、資本資産価格価格モデル(CAPM)の考え方に基づく。
このようにグラフ化されればより視覚的に、証券市場線(SML)は、株式市場におけるシステマティック・リスク(β値)と投資家の期待収益率の相関に対する予測を行うことが可能になる。
β値から期待収益率を予想できるのは、個別の証券や投資ポートフォリオはもちろんのこと、S&P500や日経平均株価やTOPIXといった投資インデックスについても同様である。
ただし、個別の証券や投資ポートフォリオについては、常に証券市場線(SML)上にプロットされるとは限らない。
短期的には、株価が過大評価されれば、証券市場線より大きく下方に乖離し、株価が歌唱されていれば、証券市場線より大きく上方に乖離する可能性がある。
上場株式(公開株式)である以上、売買取引は常時行われているため、そうした時価評価額の激しく細かい変動は、理論値である証券市場線から乖離しがちになることも知られている。
※ histrical volatility でβ値を計算する帰納法的アプローチでは、こうした瞬時の乖離は全てを防ぐことはできない。もし、恒常的に特定の銘柄について株価の過小評価または過大評価が起こっている場合は、投資家からの「期待収益率」の方が見直されて新しい値になっていることが多い。なぜなら、βは過去実績から計算される経験則(経験値)であるため、将来に向かった投資家の予測値である「期待収益率」の方を上下に調整することで、市場全体のCAPM理論が成立する(SMLがきちんと描かれる)ことになるからだ。もちろん、historical volatility を用いる分析手法には、鶏が先か卵が先か、異論は多々ある。それについては別稿で扱うこととする。
証券市場線(SML)の形の意味
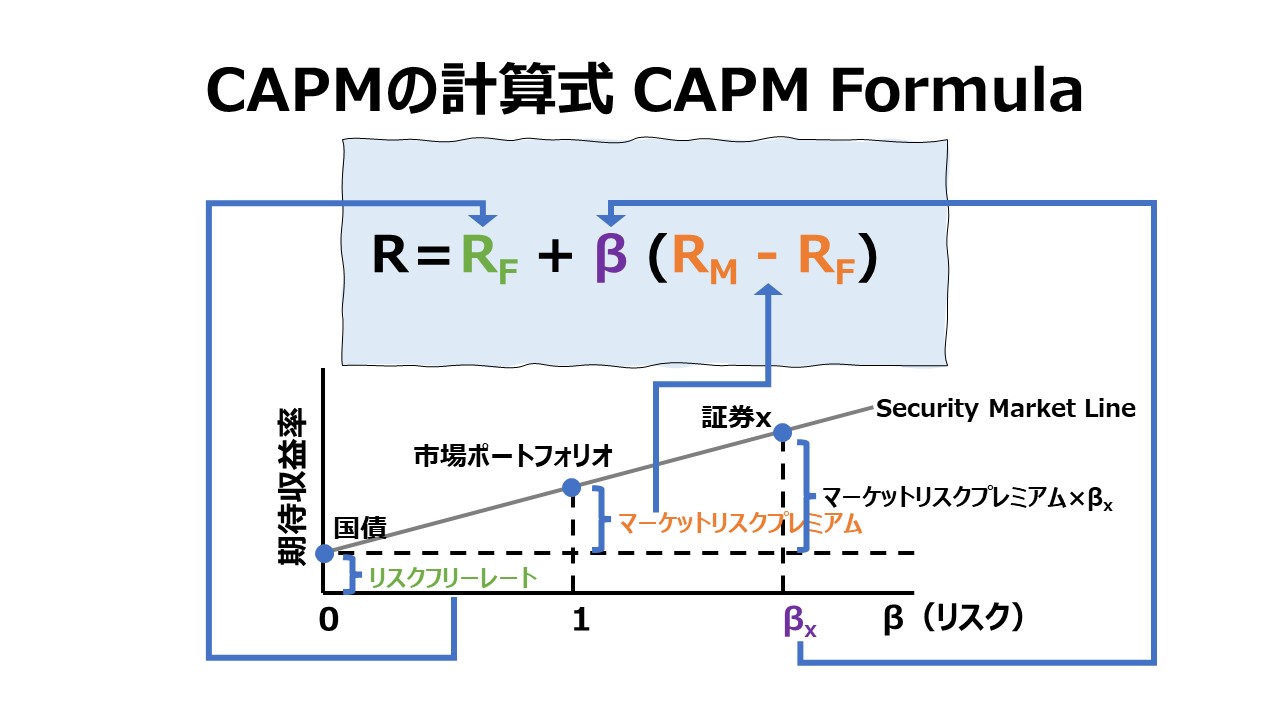
証券市場線(SML)は、リスクフリーレートでy軸と交差することになる。この時、x軸はゼロでそれは、β=0を意味する。β=0はリスクフリーレートを有する投資機会(実質的には米国債を意味する)だから、証券市場線(SML)がy軸と交差する点の高さが、その時のリスクフリーレートである投資機会の目標収益率(米国債の場合は利回り)となる。
このことは同時に、投資機会を与える証券投資のβ値(システマティック・リスク)がゼロであるならば、投資家の目標利益率はお金の時間価値(value of money)だけから構成されることになる。
※ なぜなら、目標利益率に加えられるべきリスクプレミアムは、投資家が負うべきリスク(≒システマティック・リスク、β値)に見合ったものになるべきだから。リスクフリーレートの投資機会にはシステマティック・リスクが無いので、当然、見返りとしてのリスクプレミアム(利回りの上乗せ)は生じない。
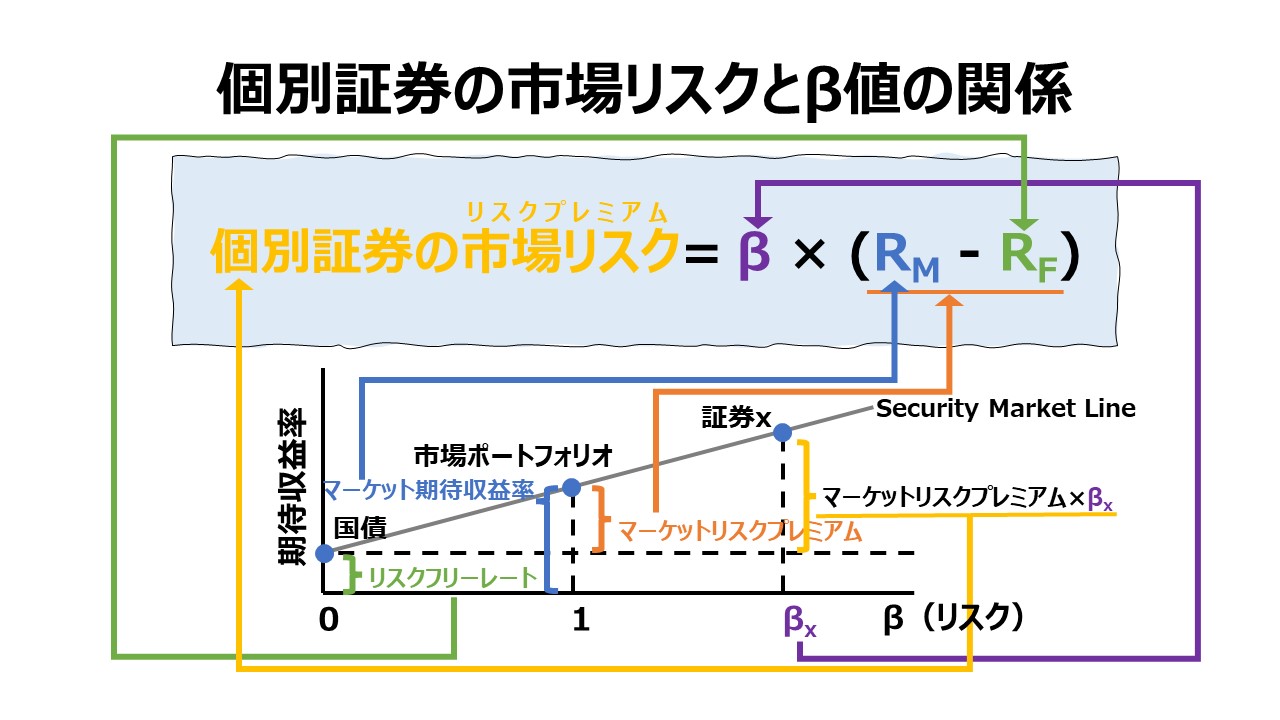
投資家が市場全体より高い価格変動性を持つ個別証券に投資することで被る可能性がある価格変動リスクを打ち消すために、価格変動リスクがゼロであるリスクフリーレートを持つ証券の利回りより高い利回りを要求することは普通の投資行動である。
このリスクフリーレートに上積みされて要求される利回り(リターン)のことをリスクプレミアムと呼ぶが、このリスクプレミアムは、価格変動リスク=システマティック・リスク=β値がより大きくなればなるほど、より高いリターンとして要求されるものだ。
したがって、証券市場線(SML)は、y軸とリスクフリーレートの高さで交差した後、x軸のβ値が増えれば増えるほど、右肩上がりで伸びていくことになる。
証券市場線(SML)上の特定の点は、その点で、システマティック・リスク(β値)と投資家からの目標収益率(リターン)が丁度釣り合うポイントを表すことになる。
証券市場線(SML)を描く
証券市場線(SML)の形状についてその特徴をまとめる。
- y切片(x=0のとき、y軸と交差するときのyの値)は、リスクフリーレートを意味する
- x軸上でβ=1のとき、yの値は、そのときの証券市場全体の必要収益率(目標収益率)である
- 証券市場線の傾きは、そのときの市場リスクプレミアム(マーケットリスクプレミアム)である
ここでは、証券市場線(SML)は回帰直線(1次式)で与えられているという大前提がある。1次直線の場合は、その直線上のいかなる(x,y)の組み合わせをとってきても、直線の傾きは常に同じである。
\( \displaystyle \bf 直線の傾き=\frac{Δy}{Δx} \)
上式で、ΔyとΔxは、x2>x1のとき、この直線上にある(x1,y1)と(x2,y2)という2つの座標が与えられれば、
\( \displaystyle \bf 直線の傾き=\frac{Δy}{Δx} = \frac{y_2-y_1}{x_2-x_1}\)
とすることで求めることができる。
このことは、❶リスクフリーレート と ❷証券市場全体の必要収益率の2つが分かれば、市場リスクプレミアムも分かることを意味する。
リスクフリーレートが0.5%、証券市場全体の必要収益率が4.0%のとき、リスクフリーレートのβ=0、集権市場全体のβ=1だから、リスクフリーレートの証券市場線上における座標は(0, 0.5%)、証券市場全体の証券市場線上における座標は(1, 4.0%)とおけるので、
\( \displaystyle \bf 直線の傾き=\frac{Δy}{Δx} = \frac{y_2-y_1}{x_2-x_1} = \frac{4-0.5}{1-0}=\frac{3.5}{1}=3.5\)
となり、市場リスクプレミアムが3.5であるということが判明した。
ファイナンシャルマネジメント Financial Management
コメント