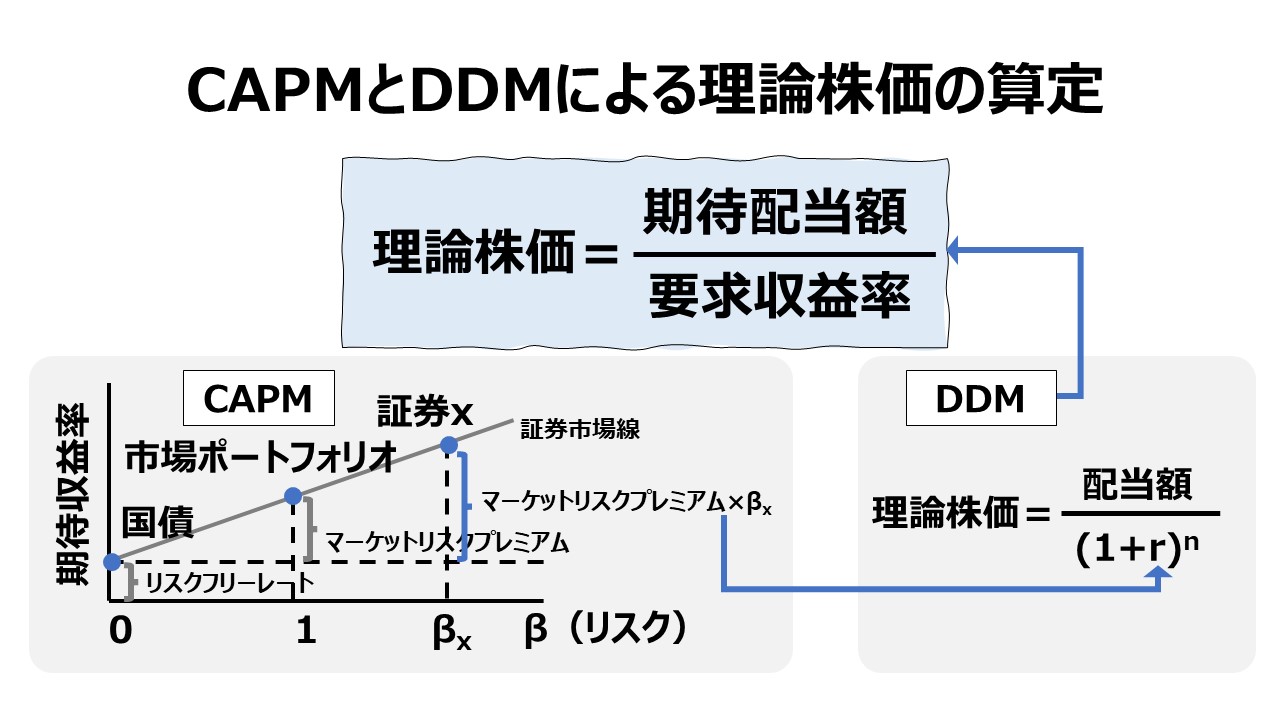
CAPMとDDMによる理論株価の算定
CAPMと配当割引モデル(DDM)
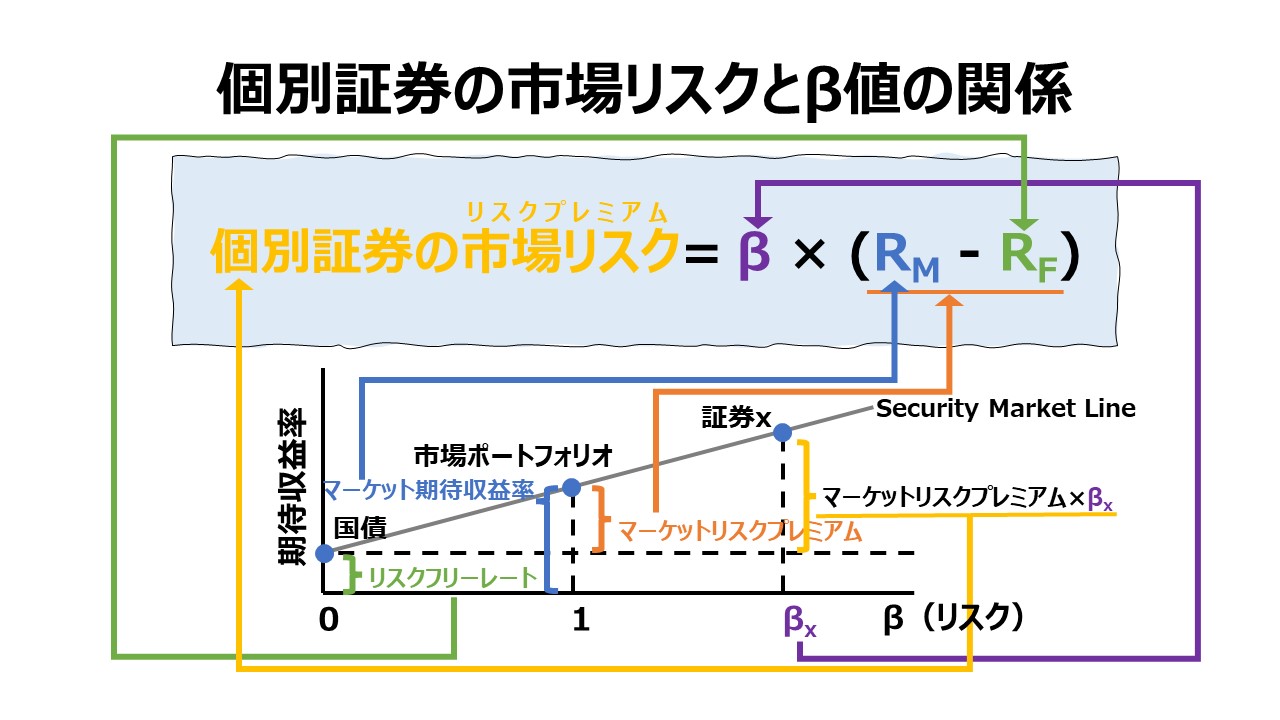
CAPMにより個別証券に対する要求収益率(目標収益率)を推計することができる。
これを個別株式に当てはめて理論株価を求めようとするときに用いられるのが「配当割引モデル(DDM: Dividend Discount Model)」である。
要求収益率(目標収益率)を用いることで、個別株式の本質的価値/公正価値(intrinsic value, fair value)を算定する。
株式の本質的価値/公正価値は、配当金の形で支払われる将来の期待キャッシュフローの総合計額を要求収益率(目標収益率)で割り引くことで、あるべき理論株価を求める。
これと株式市場における実際の株価とを比較することで、現在の株価が割高なのか割安なのかを推し量ろうというものである。
株価の理論値はその株を持ち続けた場合に将来支払われる配当の現在価値の合計値であるとする考え方から導かれる。割引現在価値を計算する際に使用される割引率に、CAPMで計算される要求収益率(目標収益率)を採用するのである。
要求収益率(目標収益率)と期待収益率
※ 言葉の定義
- 要求収益率(目標収益率):required rate of return
- 投資家が同じ市場リスクに直面する証券に対して等しく要求する利回り
- CAPM等、ある理論やモデルに従って導かれる一般解
- 期待収益率:expected rate of return
- 実際にその証券投資から得られる利回り
- 株式市場での特定日時における実際株価を用いて導かれる特殊解
株式市場におけるミスプライシング(値付けの間違い)が無ければ、理論株価=実際株価となり、要求収益率=期待収益率となり、何ら問題は生じない。
しかし、いかに効率的な株式市場であっても、極短期的には価格変動(大きな振れ、モメンタム等)により、実際の利回りが理論値を大きく上下に外れる場合がある。
ファンダメンタルズ分析では、実勢値と理論値の差を明らかにして、割安株・割高株を洗い出すことを目的としている。そのため、最初から、ミスプライシングが起こり得ることを前提とした株価評価手法である。
日本語の区別としては、CAPMなどの理論や一般的な投資家の評価視点から要求されて当然の収益率だから「要求収益率」、購入者の立場から見て期待できる、実際の株価から算出された「期待収益率」というふうに、こじつけてでも呼び名を分けておくことを意識付けしておいた方がよい。
ただし、翻訳本や日本人の論文・投資コラムなどでは、両者の混同が多発しているため、読者側が文脈から両者の違いを意識して解読する姿勢が常に必要になる。
配当割引モデル(DDM) の種類
期待収益(配当額)と要求収益率/目標収益率(割引率)に対する仮定を色々と工夫することで、下記のようにDDMを活用した理論株価の求め方にはいくつかの手法が存在する。
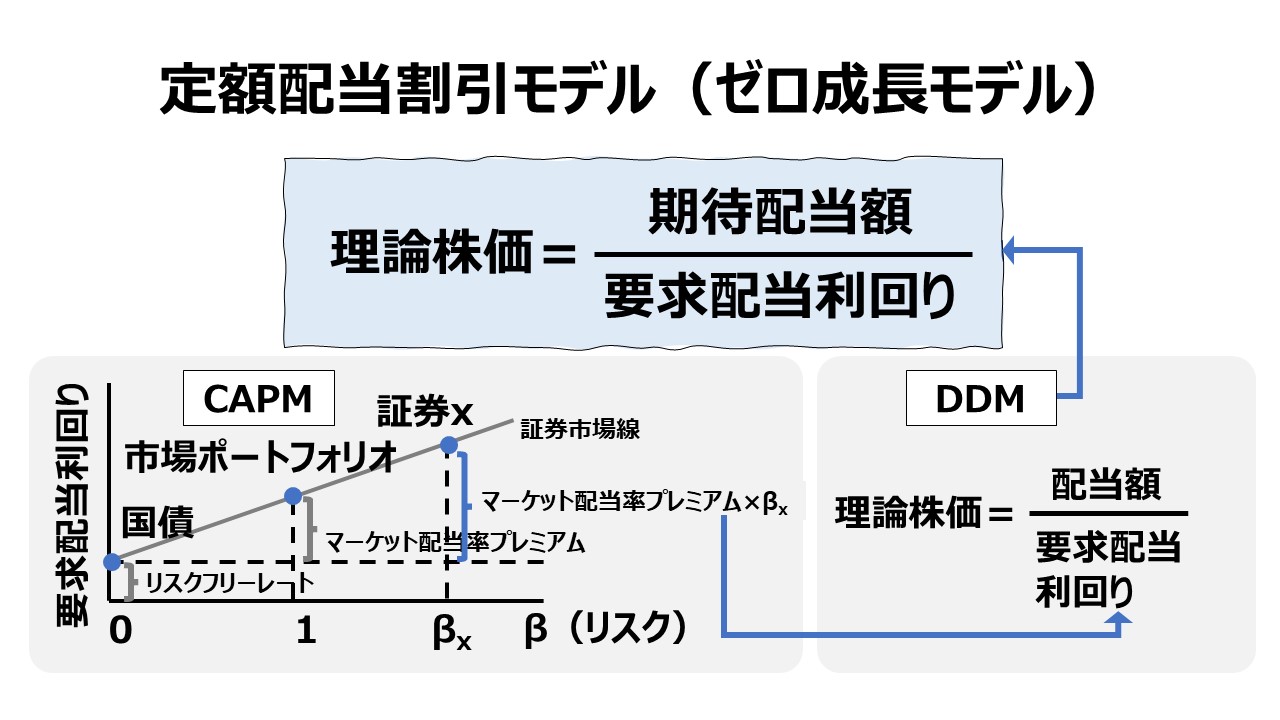
定額配当割引モデル(ゼロ成長モデル)
- 将来にわたって一定額の配当が続くという仮定
- 終身年金(perpetual annuity)の計算式をモデルにする
\( \displaystyle \bf 理論株価=\frac{配当額}{要求収益率} \)
定率成長配当割引モデル
- 将来にわたって一定率で配当が成長していくという仮定
- 割引率から配当成長率を控除する
\( \displaystyle \bf 理論株価=\frac{配当額\times(1+成長率)}{要求収益率-成長率} \)
二段階成長配当割引モデル
- 配当が急成長する期間と安定成長する期間の2ステージに分けられるという仮定
- 下記は、急成長期間と安定成長期間それぞれの基準配当額と成長率が固定されている場合の計算式
\( \displaystyle \bf 理論株価=D_1 \times \sum_{t=1}^m \frac{(1+g_{1})^{t-1}}{(1+r)^t}+D_m \times \sum_{t=m+1}^n \frac{(1+g_{2})^{t-m}}{(1+r)^t} \)
多段階成長配当割引モデル
- 割引率が異なる期間ごとに計算された各期の割引現在価値の総合計が理論株価となるという仮定
\( \displaystyle \bf (バリエーションが多いためここでの計算式の例示は割愛) \)
コメント