- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算式
売上高成長率は、基準時点からの売上高の増減比率で、一般的には事業の拡大または縮小を時系列で捉える際に利用される。
単純な2時点間の成長率は、いわゆる単利計算で求めることができる。
\( \displaystyle \bf 売上高成長率＝ \frac{売上高変化額}{基準年の売上高} \times 100\% \)
例えば、基準年の売上高が100で、売上高変化額が+40だとしたら、
\( \displaystyle \bf 売上高成長率＝ \frac{40}{100} \times 100\% \)
\( \displaystyle \bf 売上高成長率＝ 40\% \)
という割り算だけで成長率を求めることができる。
しかし、この売上成長が4年間かけて実現されたとしたら、毎年の平均的な売上高成長率はどれくらいになるのかを知りたくなる。
40%÷4年＝10%/年
残念ながら、上式は数学的には間違いである。
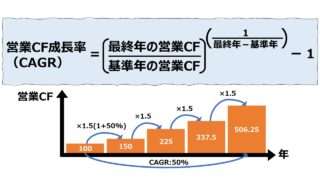
背理法で説明すると、もし、10%の成長率で100の売上高が4年間成長し続けるとしたら、
1年後：100×(100% + 10%)=110
2年後：110×(100% + 10%)=121
3年後：121×(100% + 10%)=133.1
4年後：133.1×(100% + 10%)=146.41
4年かけて、100の売上高が146.41になるので、
\( \displaystyle \bf 売上高成長率＝ \frac{46.41}{100} \times 100\% \)
\( \displaystyle \bf 売上高成長率＝ 46.41\% ≠ 40\% \)
40%を4で割るのは、算術平均（足し算したものを数量で割る）の考え方だが、今年の成長率が前年の売上高と掛け算されて今年の売上高が求められるので、掛け算の結果の平均は、幾何平均（掛け算した合計のn乗根を取る）で求める必要がある。
上記の各年度の対前年売上高成長率が全て10%で、これが4期続くのだから、
\( \displaystyle \bf 年平均売上高成長率＝ \sqrt[4]{10\% \times 10\% \times 10\% \times 10\%} \)
\( \displaystyle \bf 年平均売上高成長率＝ \sqrt[4]{0.0001} \)
\( \displaystyle \bf 年平均売上高成長率＝ 10\% \)
ここから、幾何平均で年平均成長率を求めるやり方を、公式化したものを示す。
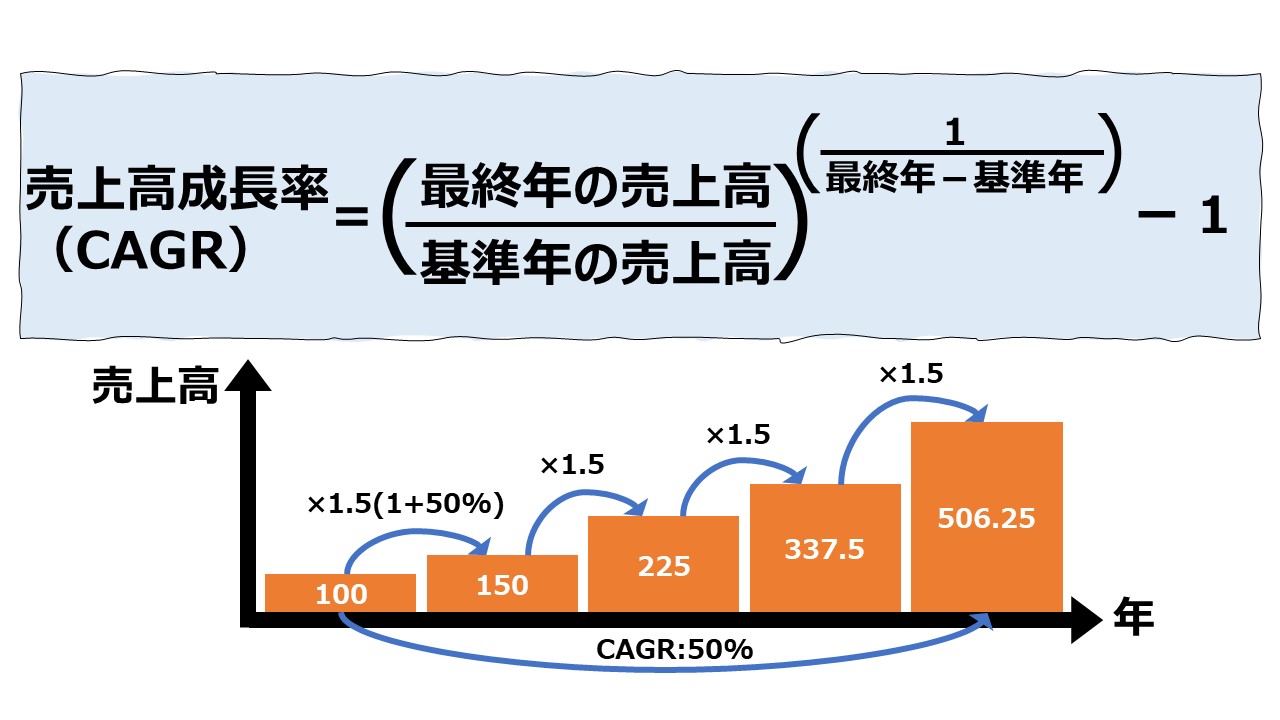
\( \displaystyle \bf 年平均売上高成長率(\%)＝ \left( \frac{ｎ年の値}{基準年の値} \right)^{\frac{~~~~~~~~~~1~~~~~~~~~~~~~~~}{n年-基準年~~~~}}-1 \)
この時、基準年＝１（年目）と置くことができれば、
\( \displaystyle \bf 年平均売上高成長率(\%)＝ \left( \frac{ｎ年の値}{基準年の値} \right)^{\frac{1}{n-1}}-1 \)
と記述することができる。
最初は「n-1」の意味が分からずこの公式の使いまわしに苦慮することが多い。
基準年から5年後までの年平均成長率を求めたい場合、基準年を含めると6期間（6年間）の平均をとることになる。
基準年は初年度で、基準年自体に成長率は設定されないから、6期間（6年間）の平均は、5つの数字の平均をとることになる。だから、この場合は、ｎ=6 で、n-1=5となる。
ちなみに、2021年が基準年で、2025年が最終年だとしたら、
2025 – 2021 = 4
実際に売上高成長率が計算されるのは、2022年、2023年、2024年、2025年の4期間（4回）なので、この場合の幾何平均のn乗根は、4乗根で計算することになる。
最初から、基準年から翌年の2年目は最初の成長率を数える一つ目の年、という風に数える脳の癖がある場合、最初から n-1 の数を脳内にイメージしていることになる。
この幾何平均でもって年平均成長率を計算する方式は英語で、CAGR: Compound Annual Growth Rate となる。
ちなみに、「Annual」は「Average」と間違いやすい。
さらに、年平均ではなく、月平均や四半期平均、日次平均は求めることができるかと考えを進めると、要は成長率をカウントする期間数のみが重要なので、回答から言うと、期間数の計量単位が年/半期/四半期/月次/日次と変わるだけで、公式自体は変わらない。
但し、日利（日歩）や月利を年利換算しないと皮膚感覚に合わない方は、最初から年利換算した数値を用いた方が無難である。
※別途、年利⇔日歩・月利等の変換方法の解説をする予定
定義と意味
年平均成長率（CAGR）による売上高成長率は、年平均をとる期間の長短にもよるが、一般にその企業のビジネス規模（事業規模）の成長スピードを示す。
この成長率は「名目成長率」として、インフレーション（簡単に言うと物価変動）の影響を含んで計算することが多い。
名目成長率として用いることで、利子率や世の中の経済成長率（GDP成長率など）と比較しやすくなる。
売上債権回収期間は複数年のスパンで見る成長率を議論する場合は度外視（無視）する方が分かりやすい。
そうすると、売上高はその企業の本業における収入額を表すことから、その企業の収益の成長スピードそのものを示し、とりあえずビジネスから手にすることができる現金が増えるスピードを意味する。
一般的には、売上高が増加すればするほど、儲けとなる収益（≒収入）も増えることから、売上高成長率が高水準で保持されることは歓迎される傾向にある。
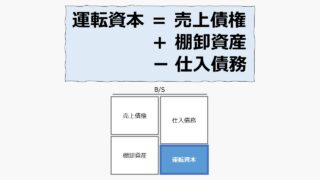
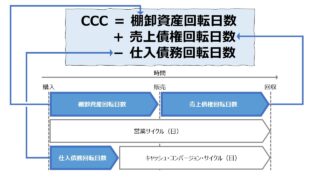
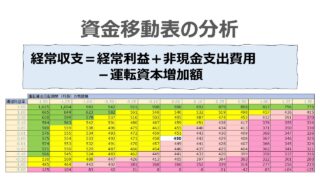
ただし、売上高が増加すると、その売上高を生み出すだけのビジネスを回転させるために必要とする運転資金（運転資本）も同率だけ増加することが多い。
急激な売上高成長は、ビジネス規模の拡大、知名度の上昇、シェアの拡大から競争優位なポジションの強化などといった歓迎すべき点より、運転資金不足による「黒字倒産」のリスクも高まることについて十分に配慮した方がよい。
解釈と使用法
成長率の解釈
普通に財務諸表における売上高の数値を用いて計算すれば、「名目成長率」として売上高成長率の数字が求められる。
仮に、企業が自社が対面する市場が国内市場（日本のみ）であったとしても、最低限、自社の売上高成長率は世界経済成長率（名目）の 3～5%は欲しいところである。
理由は、直接には国内市場を対象としたビジネスであったとしても、競争は必ずグローバル市場で行われているからである。
❶国内に所在する顧客は、個人・法人を問わず、顧客自身の収入はグローバル市場から得ているかもしれない。
❷国内市場だからと言って、外国企業の参入を阻止されて、100%輸入分が無いとは限らない。
❸資本の論理はグローバル市場を前提に機能しているため国別の例外は存在しない。
❶について、自社の国内顧客が輸出や海外子会社から収入を得ているとしたら、顧客の購買力はグローバル市場の成長率に伴って同率分大きくなっているはずである。
その中で、日本国内がほぼゼロ成長率だから、自社の売上高成長率もゼロでいいと安閑としていると、顧客の購買力の成長していくにつれて、自社の購買力内シェアが低下していくのを看過するのと同義となる。
❷について、短期的には強固な関税障壁により、海外市場から守られているとしても、中長期的にはいずれ市場開放が実現してしまうかもしれない。
市場競争にさらされて自社を鍛え続けていないと、いったん市場開放がなされ、安価で高品質な輸入品が入ってきた途端に顧客を失いかねない。
❸について、財市場、労働市場を海外から閉ざすことができたとしても、資本市場を完全にクローズすることは不可能である。
世界経済成長率が3～5%であり、株式資本（エクイティファイナンス）が求める利益率は8%前後である。
地球上でビジネスをしている以上、3～8%程度の成長を毎年遂げていないと、世間一般の購買力の成長率に負けていることになり、実質、ゼロ成長どころかマイナス成長となってしまう。
よって、CAGRによる売上高成長率は、世界経済成長率（名目成長率）が最低限達成すべき下限を示してくれているという意味で、
逆に、世界経済成長率（名目）を上回っている場合は、
使用法
大別して、3つの活用法が考えられる。
❶コンペチターとCAGRによる売上高成長率を比較し、自社の市場競争力を推し量る
❷過去実績におけるCAGRによる売上高成長率を検証し、予実分析の視点から過去施策の良否を判定する
❸CAGR計算をベースに将来予測を行う
❸について、CAGRの公式から、計算要素は、「基準年の売上高」「n年目の売上高」「ｎ年目（n-1年後）」「CAGR」の４つである。
「基準年の売上高」はそもそものCAGR計算の基礎なので常に与えられるとして、他の2変数が与えられれば、代数の基礎知識から、残りひとつの変数は求めることができる。
よって、❸の将来予測は、以下の3パータンから選ぶことができる。
| ＃ | 予測したい値 | 前提となる変数 |
|---|---|---|
| １ | 目標CAGR | 基準年の売上高、目標売上高、年数 |
| ２ | 達成可能売上高 | 基準年の売上高、目標CAGR、年数 |
| ３ | 目標達成必要年数 | 基準年の売上高、目標売上高、目標CAGR |
シミュレーション
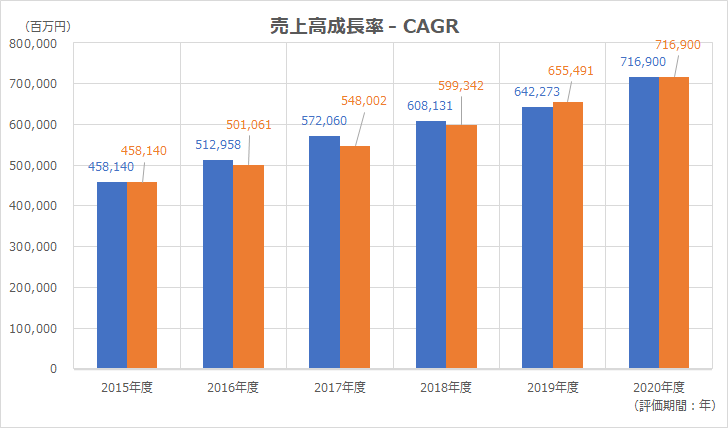
以下に、Excelテンプレートとして、FY15～FY20のニトリホールディングスの実績データをサンプルで表示している。
入力欄の青字になっている「評価期間（年）」「売上高」に任意の数字を入力すると、表とグラフを自由に操作することができる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
テンプレートの使用方法
【グラフ】過去チェック
「過去チェック」とあるが、年別に立案した中期事業計画をCAGR成長率のものと比較するケースでも使用できる。
要は、CAGR成長率が示す巡航速度と、各期の実績値または計画/予測値のズレを明らかにするものである。
サンプルとして表示しているニトリホールディングスの場合、CAGR成長率が示す巡航速度より、基準年に近い前半期間（FY16-18）の実績値の方が高くなっている。
これは、ニトリホールディングスの売上高成長がリニアに近い線で実現されていることを意味している。
この事実が示唆することは2つある。
❶ 計画期の後半部分の加速を頼みにするホッケースティックの形ではないため、より健全な成長軌道である
❷ 既存店売上高の増大より、新規店舗出店による拡販実現によるものである可能性が高い
CAGRは、複利計算と同質なので、利息に利息が付く構造のため、評価期間の後半部分の成長率の方が前半部分より高くなる。
すなわち、一般的には下に凸の曲線の形状（もちろん指数関数）になる。
これがリニアになっていることは、より早期に成長を実現していることを意味している。
リニアに成長しているということは、あまり複利効果が発揮されていないことを同時に示唆する。チェーンストアにとっての複利効果は既存店の拡販に他ならない。
出店ペースが毎年同じ場合、売上成長率もまた毎年同じ数字になる。
ちなみに、途中経過年において、前年対比で売上高が減少した場合でも、評価年を通した年平均成長率（CAGR）は変わらないし、CAGRの計算が狂うこともない。
また、基準年の売上高より最終年度の売上高が減少した場合は、計算されるCAGRはマイナス値をとる。
その場合でも、途中経過年の実績値（または計画/予測値）がきちんと設定されていれば、CAGRから導かれる巡航速度との比較が可能である。
シミュレーション
前章で解説した通り、CAGRの公式から、代数計算を用いることで、与件となる変数が分かれば、残りのひとつを求めることができる。
上から順に、「目標CAGR」「達成可能売上高」「目標達成必要年数」を求める計算式をグラフ付きで表示している。
なお、３つとも同じ結果に似せるための端数調整を「CAGR」で行っているため、CAGRの小数点以下を10桁表示している。
折れ線グラフについては、VBA/マクロを用いずに描画するために、任意の最終年が選ばれても、必ず間に7つの経過年を自動にプロットするようにスプレッドシート計算だけで組んである。
評価期間が10年程度では折れ線グラフに歪さが残るが、15～20年程度の期間をとると違和感がなくなってくる。
【参考】使用しているExcel関数
CONCAT関数、COUNTA関数、LOG関数、ROUNDUP関数
参考サイト
同じテーマについて解説が付され、参考になるサイトをいくつか紹介しておく。
![[財務諸表分析]比率分析指標の体系と一覧](https://management-accounting.biz/wp-content/uploads/2020/07/financial-analysis-system.jpg)
[財務諸表分析]比率分析指標の体系と一覧
| 1 | 財務諸表分析の理論 | 経営分析との関係、EVAツリー |
| 2 | 成長性分析（Growth） | 売上高・利益・資産成長率、持続可能成長率 |
| 3 | 流動性分析（Liquidity） | 短期の支払能力、キャッシュフロー分析 |
| 4 | 健全性分析（Leverage） | 財務レバレッジの健全性、Solvency とも |
| 5 | 収益性分析（Profitability） | ROS、ROA、ROE、DOE、ROIC、RIなど |
| 6 | 効率性分析（Activity） | 各種資産・負債の回転率（回転日数）、CCC |
| 7 | 生産性分析（Productivity） | 付加価値分析、付加価値の分配 |
| 8 | 市場指標（Stock Market） | 株価関連分析、株主価値評価 |
コメント