概要
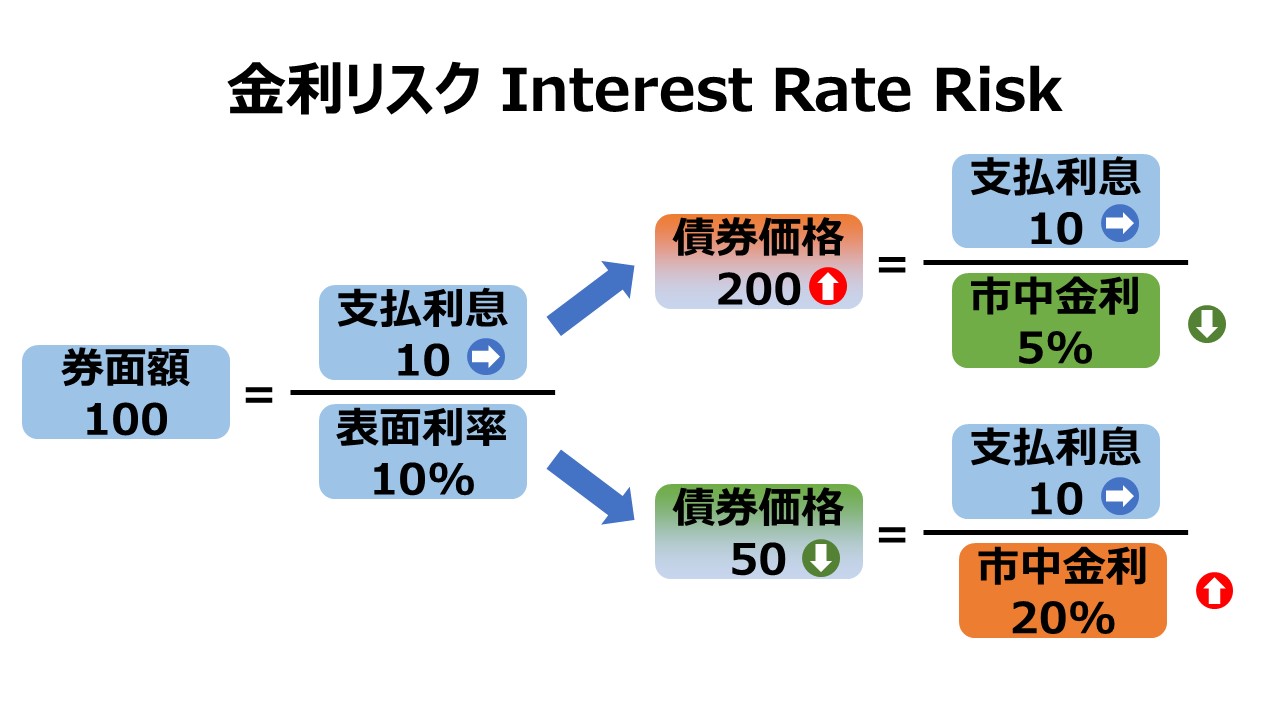
金融市場での金利の変化がもたらす投資価値の変化のことを金利リスクという。投資対象が金融商品の場合は、往々にしてその金融商品の価格(時価)が変わってしまうことから、価格リスク(price risk)と呼ばれることもある。
市場金利より低い利息しか支払われない投資案件(金融商品)は、市場金利に見合うまで、すなわち、実効金利が市場金利に一致するまで、投資価値(金融商品の時価)が割り引かれ(時価が値下げされ)て売買されることになる。
投資商品の満期までの期間が長くなればなるほど、金利リスクは大きくなる。
したがって、長期債の価格は短期債の価格より、金利変動に対して敏感に反応することになる。
金利リスクの考え方は、固定金利でかつ流通市場(secondary market)で売買可能な債券にとって非常に重要なものとなる。なぜなら、そうした債券の売却価格すなわち時価・市場価値は、その債券から得られる将来キャッシュフロー(固定金利で支払われる利息の全てと償還される元本)の割引現在価値になっているからである。
割引現在価値を計算するために使用される割引率はその時点の市場金利となる。
仮に、市場金利が上昇したら、長期債からの利払は固定だとしても、割引率もその分上昇するため、その固定利息分の割引現在価値は減少してしまう。そのため、この長期債の魅力度(お得度)が下がってしまい、流通市場での時価もその分だけ下がってしまうことになる。
長期の固定利付である債券を用いた説明
ある債券の固定利息が額面に対し6%で、債券が売買されている流通市場における市場金利は5%だとする。
この時点で、この債券をこのまま購入すると、市場より1%有利な金利による利払を享受できる。債券市場が十分に効率的である場合、市場裁定(金利裁定)が自動で発動し、6%の固定金利を計算している根拠のひとつである債券の額面(face value)が市場金利の5%に見合うように市場メカニズムに従って価格調整され、実際の購入価額は額面より高くなる。
数年経ち、今度は市場金利が8%に上がったとする。
この債券の利回りは額面に対して6%固定であるため、今度は市場金利より2%低い利回りになってしまう。
そうすると、この債券に類似する他の投資機会(類似する長期債を購入すること)に対して魅力度(お得度)が下がってしまうことになる。そのため、市場金利(とりわけ類似の長期債)と同レベルの利回りを実現するために、額面より低い価格で売買されることになる。
つまり、市場金利が上昇すると、この債券の保有者は保有債券の元本価値をその分失うことになる。もし、この債券保有者が流通市場でこの債券を売却しようと試みたら、売却債券の実際利回りが8%となるまで、額面よりいくらか割引された価格でしか売却できないということを意味する。
言い換えると、この投資家(債券保有者)は、券面額より低い割引価格でしか保有債券を売却できないということであり、それは同時にプレミアムを付けてこの債券を購入してしまったということである。
しかしながら、この債券保有者が満期までこの長期債を保有し続ければ、満期日には額面通りの元本の償還(払い戻し)を受けることができる。但しその償還される元本は、プレミアムを付けてこの債券を購入した際の購入価額よりは少なくなっているはずだ。
確かに満期日までこの長期債を持ち続けた投資家は、券面額に基づいた6%の利払を受け続けることができる。
しかし、満期日までこの債券を保有し続けた投資家の年あたり総収益(total annual return)は、保有期間平均で5%に収斂するように元本の償還額が購入時価格より減額されるのである。
【例題】固定利付債で金利リスクを感じる
- 額面金額:100,000
- 満期:5年
- 表面利率:8%(半年)
- 発行日:2021/1/1
- 市中金利
- 2021/1/1:10%
- 2022/1/1:12%
2021/1/1時点の発行価格を求めよ
❶利息価値
利払額=100,000×8%÷2=4,000(∵2で割るのは半年ごとの利払いだから年払いの半額にするため)
満期まで5年で半期払いだから、5×2=10回が割引回数(割引期間)となる
利払額の割引現在価値は、
\( \displaystyle \bf 年金現価係数=\frac{(1+r)^n-1}{r(1+r)^n}\)
であり、r=5%(利払いが半年ごとにあるので市中金利である年利10%の半分)、n=10 なので、
\( \displaystyle \bf 利払分の割引現在価値=4,000\times \frac{(1+0.05)^{10}-1}{0.05(1+0.05)^{10}} \)
\( \displaystyle \bf =4,000 \times \frac{1.05^{10}-1}{0.05 \times 1.05^{10}} \)
\( \displaystyle \bf =4,000 \times \frac{1.628894627-1}{0.05 \times 1.628894627^{10}} \)
\( \displaystyle \bf =4,000 \times \frac{0.628894627}{0.081444731} \)
\( \displaystyle \bf =4,000 \times 7.721734929 = 30,886.93972 ≒ 30,887\)
❷元本価値
額面金額:100,000が5年後(10割引期間後)に償還されてくるのだから、その時点での市中金利10%の半分の5%でこれを10期間分(5年ではない)で割り引けばよい
\( \displaystyle \bf 元本の割引現在価値= \frac{100,000}{(1+0.05)^{10}} = \frac{100,000}{1.628894627} =61391.32535 ≒ 61,391\)
❸この債券の発行時点の割引現在価値(=発行価額)は、
\( \displaystyle \bf 債券の割引現在価値= 利息の割引現在価値+元本の割引現在価値\)
\( \displaystyle \bf 債券の割引現在価値= 30,887 + 61,391 = 92,278\)
となる。
これは、額面金額:100,000より小さい金額となるため、割引発行となる。
2022/1/1の市場価格を求めよ
❶利息価値
利払額=100,000×8%÷2=4,000(∵2で割るのは半年ごとの利払いだから年払いの半額にするため)
満期まで4年で半期払いだから、4×2=8回が割引回数(割引期間)となる
利払額の割引現在価値は、
\( \displaystyle \bf 年金現価係数=\frac{(1+r)^n-1}{r(1+r)^n}\)
であり、r=6%(利払いが半年ごとにあるので市中金利である年利12%の半分)、n=8 なので、
\( \displaystyle \bf 利払分の割引現在価値=4,000\times \frac{(1+0.06)^8-1}{0.06(1+0.06)^8} \)
\( \displaystyle \bf =4,000 \times \frac{1.06^8-1}{0.06 \times 1.06^8} \)
\( \displaystyle \bf =4,000 \times \frac{1.593848075-1}{0.05 \times 1.593848075^8} \)
\( \displaystyle \bf =4,000 \times \frac{0.593848075}{0.095630884} \)
\( \displaystyle \bf =4,000 \times 6.209793811 = 24,839.17524 ≒ 24,839\)
❷元本価値
額面金額:100,000が4年後(8割引期間後)に償還されてくるのだから、その時点での市中金利12%の半分の6%でこれを8期間分(4年ではない)で割り引けばよい
\( \displaystyle \bf 元本の割引現在価値= \frac{100,000}{(1+0.06)^8} = \frac{100,000}{1.593848075} =62,741.23713 ≒ 62,741\)
❸この債券の2022/1/1時点の割引現在価値(=市場価格)は、
\( \displaystyle \bf 債券の割引現在価値= 利息の割引現在価値+元本の割引現在価値\)
\( \displaystyle \bf 債券の割引現在価値= 24,839 + 62,741 = 87,580\)
となる。
設例から示唆されていること
債券の市場価値が、発行時の92,278から1年後には87,580に減少していることが分かる。そのもっとも大きな理由は、この債券が券面額に対して固定で年利8%の利払いをするのは変わっていないのに対し、発行時点の市中金利が10%から1年後には12%に上昇したためである。
確かに、2022/1/1にこの債券を購入した者が満期日までこの債券を保有し続けたとしたら、手にする利払いと償還元本の合計の購入価額に対する利回りは市中金利と同様の12%になっている。
この債券の発行者がデフォルトしない限り、この債券の購入者は、満期日に間違いなく100,000の償還を受け、償還日を迎えるまで、半年に1回、4,000の利払いをきちんと受け取ることができるのである。

ファイナンシャルマネジメント Financial Management
コーポレートファイナンスを英語と日本語のデュアルで学ぶことができる。
原書と和訳の両方を揃えて本格的な学習を始める前段階に活用するとよい。
コメント