- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
資金管理の全体像計算式
営業キャッシュフロー成長率は、基準時点からの営業キャッシュフローの増減比率で、一般的には収益力の成長度合いを時系列で捉える際に利用される。
営業キャッシュフローは本業からの収入を基礎とし、期間損益とは異なり、キャッシュの裏付けを持つ実在の資産でもあることから、収益性の成長に加えて財務健全性の変化を推し測る機能も併せ持つ。
単純な2時点間の成長率は、いわゆる単利計算で求めることができる。
\( \displaystyle \bf 営業CF成長率＝ \frac{営業CF変化額}{基準年の営業CF} \times 100\% \)
例えば、基準年の営業CFが100で、営業CF変化額が+40だとしたら、
\( \displaystyle \bf 営業CF成長率＝ \frac{40}{100} \times 100\% \)
\( \displaystyle \bf 営業CF成長率＝ 40\% \)
という割り算だけで成長率を求めることができる。
投資の時間価値（金利相当部分）を考慮しない短期（単期）の成長性分析、例えば、対前年比率を見る場合は、この単利計算による成長率で事足りる。
しかし、この営業CF成長が4年間かけて実現されたものだとしたら、毎年の平均的な営業CF成長率はどれくらいになるのかを知りたくなる。それは決して対前年比率では分からないからである。
40%÷4年＝10%/年
残念ながら、上式は数学的には間違いである。
背理法で説明すると、もし、10%の成長率で100の営業CFが4年間成長し続けるとしたら、
1年後：100×(100% + 10%)=110
2年後：110×(100% + 10%)=121
3年後：121×(100% + 10%)=133.1
4年後：133.1×(100% + 10%)=146.41
これは、4年かけて、100の営業CFが146.41になるので、
\( \displaystyle \bf 営業CF成長率＝ \frac{46.41}{100} \times 100\% \)
\( \displaystyle \bf 営業CF成長率＝ 46.41\% ≠ 40\% \)
40%を4で割るのは、算術平均（足し算したものを数量で割る）の考え方だが、今年の成長率が前年の営業CFと掛け算されて今年の営業CFが求められるので、掛け算の結果の平均は、幾何平均（掛け算した合計のn乗根を取る）で求める必要がある。
上記の各年度の対前年営業CF成長率が全て10%で、これが4期続くのだから、
\( \displaystyle \bf 年平均営業CF成長率＝ \sqrt[4]{10\% \times 10\% \times 10\% \times 10\%} \)
\( \displaystyle \bf 年平均営業CF成長率＝ \sqrt[4]{0.0001} \)
\( \displaystyle \bf 年平均営業CF成長率＝ 10\% \)
ここから、幾何平均で年平均成長率を求めるやり方を、公式化したものを示す。
\( \displaystyle \bf 年平均営業CF成長率(\%)＝ \left( \frac{ｎ年の値}{基準年の値} \right)^{\frac{~~~~~~~~~~1~~~~~~~~~~~~~~~}{n年-基準年~~~~}}-1 \)
この時、基準年＝１（年目）と置くことができれば、
\( \displaystyle \bf 年平均営業CF成長率(\%)＝ \left( \frac{ｎ年の値}{基準年の値} \right)^{\frac{1}{n-1}}-1 \)
と記述することができる。
最初は「n-1」の意味が分からずこの公式の取りまわしに苦慮することが多い。
基準年から5年後までの年平均成長率を求めたい場合、基準年を含めると6期間（6年間）の平均をとることになる。
基準年は初年度で、基準年自体に成長率は設定されないから、6期間（6年間）の平均は、5つの数字の平均をとることになる。だから、この場合は、ｎ=6 で、n-1=5となる。
ちなみに、2021年が基準年で、2025年が最終年だとしたら、
2025 – 2021 = 4
実際に営業CF成長率が計算されるのは、2022年、2023年、2024年、2025年の4期間（4回）なので、この場合の幾何平均のn乗根は、4乗根で計算することになる。
最初から、基準年から翌年の2年目は最初の成長率を数える一つ目の年、という風に数える脳の癖がある場合、最初から n-1 の数を脳内にイメージしていることになる。
この幾何平均でもって年平均成長率を計算する方式は英語で、CAGR: Compound Annual Growth Rate となる。
ちなみに、「Annual」は「Average」と間違いやすい。
さらに、年平均ではなく、月平均や四半期平均、日次平均は求めることができるかと考えを進めると、要は成長率をカウントする期間数のみが重要なので、結論から言うと、期間数の計量単位が年/半期/四半期/月次/日次と変わるだけで、公式自体は変わらない。
但し、日利（日歩）や月利を年利換算しないと皮膚感覚に合わない方は、最初から年利換算した数値を用いた方が無難である。
※別途、年利⇔日歩・月利等の変換方法の解説をする予定
定義と意味
年平均成長率（CAGR）による営業CF成長率は、年平均をとる期間の長短にもよるが、一般にその企業のビジネス規模（事業規模）の成長スピードというより、収益性と財務安定性の変化の度合いを表すと見た方が良い。
売上高のいち早い成長を望んで、スキミングプライス戦略ではなく、市場シェアの早期獲得を狙いとして、敢えて低価格を設定するペネトレイティング戦略を選択した場合、売上成長より利益成長が後ズレしていく。
（実際には、特定の価格戦略を意識しなくても、収穫逓減の法則が働き、普及度が高まれば、需要意欲が飽和して市場での価格付けは低下傾向になる）
その成長ギャップが大きければ大きいほど、急激な売上成長加速を企図するばかりに、在庫投資と資金回収されない売上債権の増大による運転資本の圧迫から資金枯渇を招いて、いわゆる”黒字倒産”の危機に陥りかねない。
その点、営業CF成長率をウォッチしておけば、キャッシュの裏付けのある収入の成長率を見ることになるので、運転資本の枯渇にはいち早く気づくことができるので知らないうちに黒字倒産となる恐れはない。
なぜなら、運転資本の増減は、営業CFの計算要素のひとつになっているからである。
一方で、営業CFは、営業利益を代表とする期間損益と比べて、キャッシュの裏付けがある分、資金繰りの逼迫度への感度もよく荒あしてくれるものだから、収益性のみならず、財務健全性（財務安定性）の度合いも示してくれる。
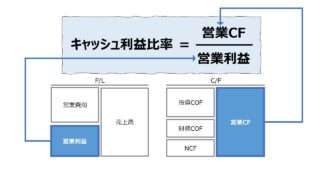
また、これは中級以上の論点だが、営業利益の成長と営業CFの成長は、得てして相反する性質を持つ。詳細は「キャッシュ利益比率（Cash to Income Ratio）」を参照して頂きたい。
解釈と使用法
成長率の解釈
営業CFの成長率自体の目安を求めるのは、業種・業態や地域別特性を考えると、一律で「●●%」だと断言することは難しい。
そこで、前章で見てきた、売上高、営業利益と営業CFの成長率を相対比較することで、財務健全性と収益性を両立する営業CFの適正値の幅を考えてみたい。
●ケーススタディ：売上成長と共に、マージンが縮小していく商材を扱う卸売業
＜条件1：通例的な数値例＞
購入単価：@10（現金仕入）
販売単価：@30（掛販売）→１年経過ごとに▲2.5
購入数量：2年目まで10個、以降は+5個/年
販売数量：1年目が5個、以降は+5個/年
債権回収期間：1年
その他経費はゼロと想定
＜商材（PSI）の動き＞
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | 5年目 |
|---|---|---|---|---|---|
| 期首在庫 | – | 5 | 5 | 5 | 5 |
| 当期仕入 | 10 | 10 | 15 | 20 | 25 |
| 当期販売 | 5 | 10 | 15 | 20 | 25 |
| 期末在庫 | 5 | 5 | 5 | 5 | 5 |
＜期間損益＞
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | ５年目 |
|---|---|---|---|---|---|
| 売上高 | 150 | 275 | 375 | 450 | 500 |
| 売上原価 | 50 | 100 | 150 | 200 | 250 |
| 利益 | 100 | 175 | 225 | 250 | 250 |
| ROS(%) | 66.7 | 63.6 | 60.0 | 55.6 | 50.0 |
＜キャッシュフロー＞
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | ５年目 |
|---|---|---|---|---|---|
| 現金仕入 | ▲100 | ▲100 | ▲150 | ▲200 | ▲250 |
| 債権回収 | 0 | 150 | 275 | 375 | 450 |
| NCF | ▲100 | 50 | 125 | 175 | 200 |
| 累積NCF | ▲100 | ▲50 | +75 | +250 | +450 |
売上高、営業利益（上記では利益と表記）、営業CF（上記ではNCFと表記）それぞれの5年目までの年平均成長率（CAGR）は、
\( \displaystyle \bf 年平均売上高成長率(\%)＝ \left( \frac{500}{150} \right)^{\frac{1}{5-1}}-1 = (3.333・・)^{\frac{1}{4}}-1 = 35.1\% \)
\( \displaystyle \bf 年平均営業利益成長率(\%)＝ \left( \frac{250}{100} \right)^{\frac{1}{5-1}}-1 = 2.5^{\frac{1}{4}}-1 = 18.9\% \)
\( \displaystyle \bf 年平均営業CF成長率(\%)＝ \left( \frac{200}{▲100} \right)^{\frac{1}{5-1}}-1 = ▲5^{\frac{1}{4}}-1 = 計算不能 \)
残念ながら、被開平数<1となるマイナスのCAGRは計算できても、被開平数が負数のCAGRは正しく計算することはできない。
※被開平数とは、 \( \sqrt[n]{x}=x^{\frac{1}{n}} \) のときの ”x” のこと
こういう場合は、単利計算（前年対比の成長率）を並べて比較分析するしかない。
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | 5年目 |
|---|---|---|---|---|---|
| 売上高成長率 | – | 83.3 | 36.4 | 20.0 | 11.1 |
| 営業利益成長率 | – | 75.0 | 28.6 | 11.1 | 0.0 |
| 営業CF成長率 | – | – | 150.0 | 40.0 | 14.3 |
単利計算による対前年成長率を並べて観察した結果、収穫逓減の法則が効いている成長過程にある企業は、数学的厳密性には欠けるが、経験則的には、
営業利益成長率 ＜ 売上高成長率 ＜ 営業CF成長率
となることが多そうである。
営業CFのCAGRを求められるようにするには、被開平数が正数になればよいから、ケーススタディにおける債権回収条件を人為的に緩やかにしてみると、
＜条件2：CAGRを妥当にする数値例＞
購入単価：@10（現金仕入）
販売単価：@30（掛販売）→１年経過ごとに▲2.5
購入数量：2年目まで10個、以降は+5個/年
販売数量：1年目が5個、以降は+5個/年
債権回収期間：一律年度末
その他経費はゼロと想定
＜商材（PSI）の動き＞
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | 5年目 |
|---|---|---|---|---|---|
| 期首在庫 | – | 5 | 5 | 5 | 5 |
| 当期仕入 | 10 | 10 | 15 | 20 | 25 |
| 当期販売 | 5 | 10 | 15 | 20 | 25 |
| 期末在庫 | 5 | 5 | 5 | 5 | 5 |
＜期間損益＞
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | ５年目 |
|---|---|---|---|---|---|
| 売上高 | 150 | 275 | 375 | 450 | 500 |
| 売上原価 | 50 | 100 | 150 | 200 | 250 |
| 利益 | 100 | 175 | 225 | 250 | 250 |
| ROS(%) | 66.7 | 63.6 | 60.0 | 55.6 | 50.0 |
＜キャッシュフロー＞
| 項目 | 1年目 | ２年目 | 3年目 | 4年目 | ５年目 |
|---|---|---|---|---|---|
| 現金仕入 | ▲100 | ▲100 | ▲150 | ▲200 | ▲250 |
| 債権回収 | 150 | 275 | 375 | 450 | 500 |
| NCF | 50 | 175 | 225 | 250 | 250 |
| 累積NCF | +50 | +225 | +450 | +700 | +950 |
売上高、営業利益（上記では利益と表記）、営業CF（上記ではNCFと表記）それぞれの5年目までの年平均成長率（CAGR）は、
\( \displaystyle \bf 年平均売上高成長率(\%)＝ \left( \frac{500}{150} \right)^{\frac{1}{5-1}}-1 = (3.333・・)^{\frac{1}{4}}-1 = 35.1\% \)
\( \displaystyle \bf 年平均営業利益成長率(\%)＝ \left( \frac{250}{100} \right)^{\frac{1}{5-1}}-1 = 2.5^{\frac{1}{4}}-1 = 18.9\% \)
\( \displaystyle \bf 年平均営業CF成長率(\%)＝ \left( \frac{250}{50} \right)^{\frac{1}{5-1}}-1 = 5^{\frac{1}{4}}-1 = 49.5\% \)
となるので、
営業利益成長率(18.9%) ＜ 売上高成長率(35.1%) ＜ 営業CF成長率(49.5%)
である。これは、条件1で見た、単利計算の対前年成長率を並べてみたものと順位は一致している。
であれば、この順位（大小関係）には、ある程度の法則が認められるのかもしれない。
まず、売上高成長率より営業利益成長率が一般的に劣後する理由は、売上成長と共に、営業費用も成長するわけだから、収益と費用をネット（相殺）して計算される営業利益の伸び率の方が売上高の伸張率に劣るのは当然の帰結である。
次に、営業利益・売上高が営業CFに劣後する理由は生半可では解読できない。
一般的な事例として挙げた、＜条件1：通例的な数値例＞にあるように、通常、キャッシュフローの採算分岐点が損益分岐点より遅くなる。どうしても売上債権の回収が収益認識よりタイミングとして遅れるからである。
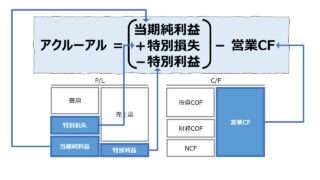
それが、アクルーアル（会計発生高）が正数を採ることが多い理由でもある。
それゆえ、事業開始直後は低く抑えられてきたネットキャッシュフローが一旦採算分岐点を超えるとこれまでのビハインドを一気に取り返し、成長率として営業利益と売上高を上回るようになるのである。
これは、事業の成長期特有の性質で、業績がシクリカル（循環的）な状態であったり、安定期に入れば、再び営業CFの成長率優位の時期は終焉を迎える。
であるから、
と見ることができよう。
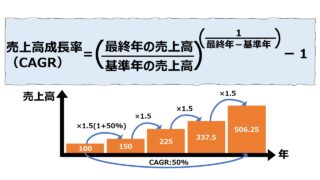
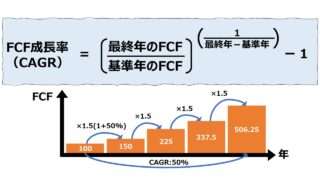
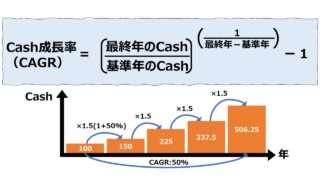
将来予測への活用法
CAGRの計算式の理解は難しくとも、変数は限られているため、変数の組み合わせ次第で、様々なシミュレーション分析に活用することは容易である。
CAGRの公式から、計算要素は、「基準年の営業CF」「n年目の営業CF」「ｎ年目（n-1年後）」「CAGR」の４つである。
「基準年の営業CF」はそもそものCAGR計算の基礎なので常に与えられるとして、他の2変数が与えられれば、代数の基礎知識から、残りひとつの変数は求めることができる。
よって、将来予測対象は、以下の3パータンから選ぶことができる。
| ＃ | 予測したい値 | 前提となる変数 |
|---|---|---|
| １ | 目標CAGR | 基準年の営業CF、目標営業CF、年数 |
| ２ | 達成可能営業CF | 基準年の営業CF、年数 、目標CAGR |
| ３ | 目標達成必要年数 | 基準年の営業CF、目標営業CF、目標CAGR |
シミュレーション
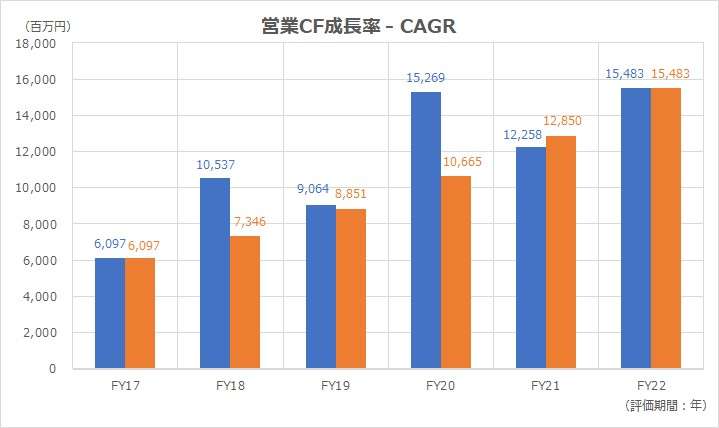
以下に、Excelテンプレートとして、FY17～FY22のＭｏｎｏｔａＲＯの実績データをサンプルで表示している。
入力欄の青字になっている「評価期間（年）」「営業CF」「売上高」「経常利益」に任意の数字を入力すると、表とグラフを自由に操作することができる。
これらの値は、EDINETにて公開されている有価証券報告書から取得したものである。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
残念ながら、僅差で 利益＜売上高＜営業CF という成長期中のピークを過ぎているようで、利益(17.36%) ＜ 営業CF(20.49%) ＜ 売上高(20.66%) と、僅かながら売上高成長率が営業CF成長率を上回るという結果になった。
過去事例から見た限り、これからの成長率は鈍化していくことが見込まれる。
テンプレートの使用方法
【グラフ】過去チェック
「過去チェック」とあるが、年別に立案した中期事業計画をCAGR成長率で機械的に算出したものと比較するケースでも使用できる。
要は、CAGR成長率が示す巡航速度と、各期の実績値または計画/予測値のズレを明らかにするものである。
サンプルとして表示しているＭｏｎｏｔａＲＯの場合、CAGR成長率が示す巡航速度より、FY18とFY20だけ、実績値が突出している。これは新型コロナ禍の影響により、在庫と売上債権が激増した期にあたる。
但し、CAGR計算期間の途中年度であるため、それらがCAGRの計算に影響を及ぼすことはない。
各年度における営業CFの実績成長率がCAGRより情報に突き抜けがちな事実が示唆する点は、非常に質が良い営業CFの成長軌道を描いている事である。
CAGRは複利計算と同質なので、利息に利息が付く構造となる。そのため、評価期間の後半部分の成長率の方が前半部分より高くなる。
すなわち、一般的には下に凸の曲線の形状（もちろん指数関数）になる。
これがリニアになっている、かつ時たま上方に突き抜けていることは、より早期に成長を実現していることを意味している。
リニアに成長しているということは、あまり複利効果が発揮されていないことを同時に示唆する。
また、基準年の営業CFより最終年度の営業CFが減少した場合は、計算されるCAGRはマイナス値をとる。
その場合でも、途中経過年の実績値（または計画/予測値）がきちんと設定されていれば、CAGRから導かれる巡航速度との比較が可能である。
シミュレーション
前章で解説した通り、CAGRの公式から、代数計算を用いることで、与件となる変数が分かれば、残りのひとつを求めることができる。
上から順に、「目標CAGR」「達成可能営業CF」「目標達成必要年数」を求める計算式をグラフ付きで表示している。過去6年間の実績をもって10年後までの予測計算に用いているため、いずれのシミュレーション結果も一致するように作成している。微妙に各年度数値がずれているのは入力したCAGRが持つ四捨五入差異による。
折れ線グラフについては、VBA/マクロを用いずに描画するために、任意の最終年が選ばれても、必ず間に7つの経過年を自動にプロットするようにスプレッドシート計算だけで組んである。
評価期間が10年程度では折れ線グラフに歪さが残るが、15～20年程度の期間をとると違和感がなくなってくる。
CONCAT関数、COUNTA関数、LOG関数、ROUNDUP関数
参考サイト
同じテーマについて解説が付され、参考になるサイトをいくつか紹介しておく。
コメント