証券市場線と株価の関係
概要
証券市場が十分に効率的でかつ個別株式が公正価値で評価されているならば、実勢株価と将来の期待配当額に基づいた投資家の期待収益率(expected rate of return)と、CAPMを用いて算定された要求収益率/目標収益率(required rate of return)はぴったり一致するはずだ。
言い換えるなら、実際株価は、期待収益率と要求収益率を一致させるように株式市場の中で決められるということだ。
割安株の価格調整メカニズムの例示
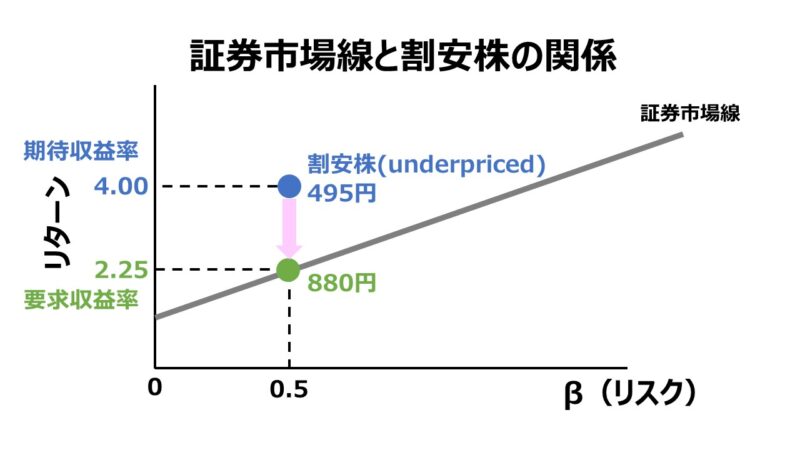
しかしながら、個別株は一時的にはミスプライスを起こし、あるべき証券市場線の上から外れることが往々にしてある。
例えば、β値が 0.5 の株式AがCAPMに基づき、要求収益率が 2.25% と計算されるとする。このとき、配当額は 19.8円だと予想されているならば、DDM(配当割引モデル)の中でも一番シンプルなゼロ成長モデルに基づくと、株式Aの理論株価は、
\( \displaystyle \bf 理論株価=\frac{配当額}{要求収益率}= \frac{19.8円}{2.25\%} =880円 \)
となる。
しかし、このときリアルの株式市場で株式Aの実際株価が495円だとしたら、
\( \displaystyle \bf 期待収益率=\frac{配当額}{実際株価}= \frac{19.8円}{495円} =4\% \)
と計算される。これをまとめると下記のようになる。
要求収益率 2.25% < 期待収益率 4% (高利回り)
理論株価 880円 > 実際株価 495円(割安 underpriced)
ここから、株式Aが証券市場線(SML: Security Market LIne)の線上に戻るためには、実際株価(495円)が切り上がって理論株価(880円)に近づき、期待収益率(4%)を要求収益率(2.25%)にサヤ寄せさせる必要が生じる。
もし、株式Aの実際株価を低く抑えている特段の理由が無いのならば、投資家たちは、株式Aの実際株価495円の中に超過利益を得る機会を発見することになるので、株式Aに対する需要が高じてやがて株式Aは理論株価である880円近傍まで上昇することになろう。
株式Aの実際株価の上昇は、株式Aに相応しいリスク許容度(それはβ値で表されている)に従って、要求収益率2.25%を達成するぎりぎりの880円にどんどん近づいていくはずだ。
逆に、880円を超えると、要求収益率2.25%より期待収益率が下回ってしまうため、株価の上昇はやがて880円で止まるはずである。
株価880円で利回り2.25%は、CAPMに導かれた与件としての証券市場線の上でβ値0.5の証券に丁度該当することになる。
注)β値が0.5の株式が常に2.25%の要求収益率であるとは限らない。あくまで例示であって、CAPMの世界観は、個別銘柄の金融的な性質の他、市場リスクプレミアムとリスクフリーレートにも左右される。
割高株の価格調整メカニズムの例示
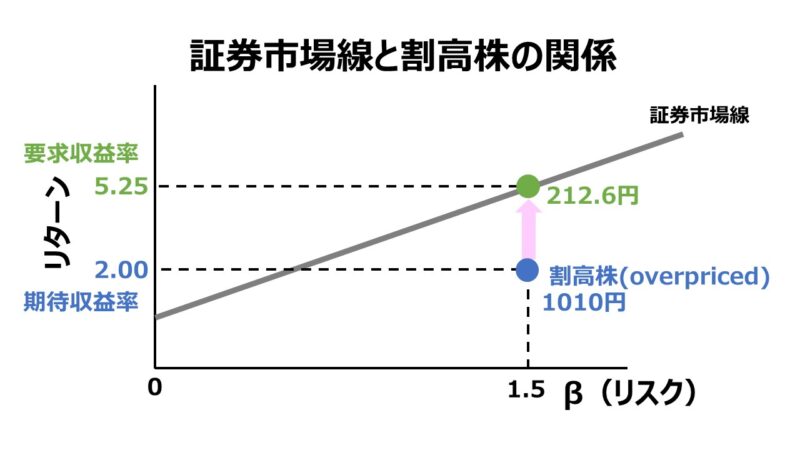
例えば、β値が 1.5 の株式BがCAPMに基づき、要求収益率が 5.75% と計算されるとする。このとき、配当額が 10.0円で毎年1%ずつ成長するものだと予想されているならば、DDMの中でも定率成長配当割引モデルに基づくと、株式Bの理論株価は、
\( \displaystyle \bf 理論株価=\frac{配当額\times(1+成長率)}{要求収益率 – 成長率}= \frac{10円\times(1+1.00\%)}{5.75\%-1.00\%} =\frac{10.1円}{4.75\%}≒212.6円 \)
となる。
しかし、このときリアルの株式市場で株式Bの実際株価が1,010円だとしたら、
\( \displaystyle \bf 期待収益率=\frac{次年度の配当額}{実際株価}+配当成長率= \frac{10円\times(1+1.00\%)}{1,010円}+1.00\% =1\%+1\%= 2\% \)
と計算される。これをまとめると下記のようになる。
要求収益率 5.25% > 期待収益率 2% (低利回り)
理論株価 212.6円 < 実際株価 1,010円(割高 overpriced)
ここから、株式Bが証券市場線(SML: Security Market LIne)の線上に戻るためには、実際株価(1,010円)が切り下がって理論株価(212.6円)に近づき、期待収益率(2%)を要求収益率(5.75%)にサヤ寄せさせる必要が生じる。
もし、株式Bの実際株価を高く留めている特段の理由が無いのならば、投資家たちは、株式Bの実際株価1,010円の中ではなく、株式B以外の銘柄に超過利益を得る機会を発見することになるので、株式Bに対する需要が減少してやがて株式Bは理論株価である212.6円近傍まで下落することになろう。
株式Bの実際株価の下落は、株式Bに相応しいリスク許容度(それはβ値で表されている)に従って、要求収益率5.75%を達成するぎりぎりの212.6円にどんどん近づいていくはずだ。
逆に、212.6円を下回ると、要求収益率5.75%より期待収益率が上回ってしまうため、株価の下落はやがて212.6円で止まるはずである。
株価212.6円で利回り5.75%は、CAPMに導かれた与件としての証券市場線の上でβ値1.5の証券に丁度該当することになる。
注)β値が1.5の株式が常に5.75%の要求収益率であるとは限らない。あくまで例示であって、CAPMの世界観は、個別銘柄の金融的な性質の他、市場リスクプレミアムとリスクフリーレートにも左右される。
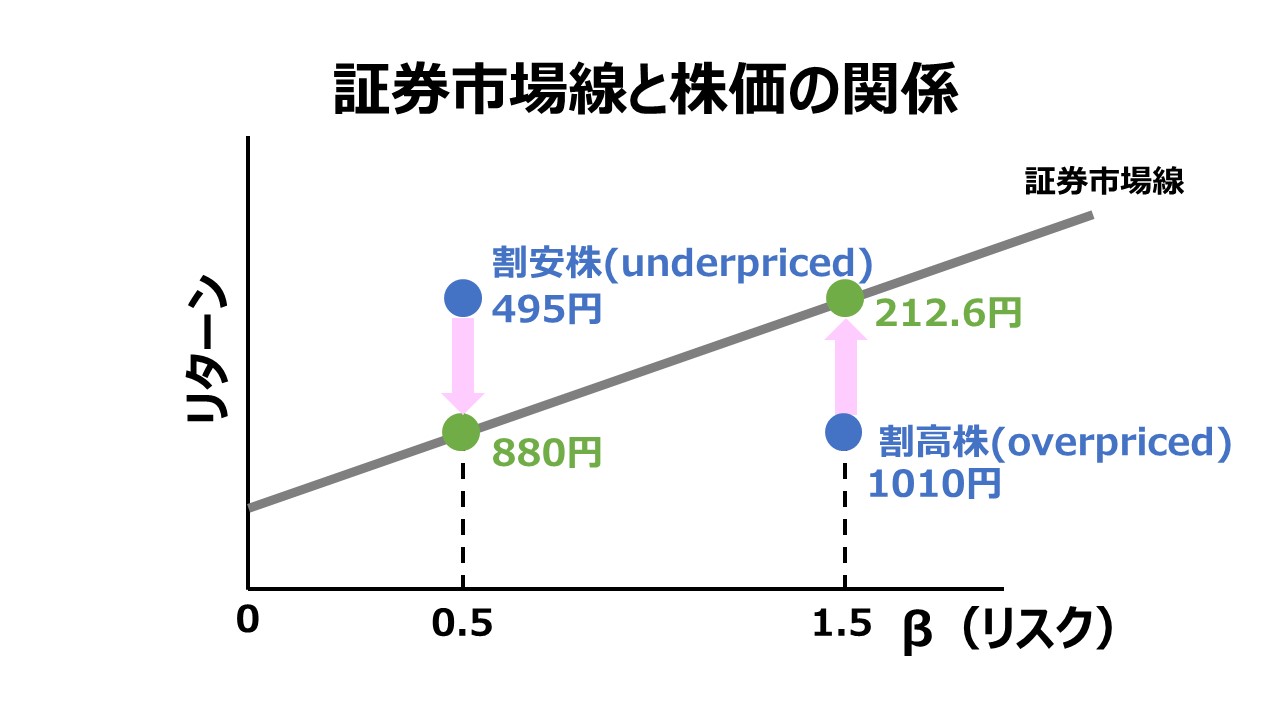
証券市場線(SML)上の均衡点
上記の例で用いた株式Aや株式Bの期待収益率が株価調整により要求収益率に再び収斂していけば、株式Aや株式Bは証券市場線(SML)上のリスクとリターンが見合った均衡点(equilibrium)に回帰することができる。
CAPMに基づけば、個別株式が均衡点から外れることはそう長く続かない。株価調整が必ず起こり、均衡点に速やかに回帰する。しかしながら、一時的な割安(underpriced)は、ロングポジション(現物を買うこと)の立場からすれば買い出動の良い投資機会になるし、一時的な割高(overpriced)は、ショートポジション(信用売り)の立場からすれば、売り出動の良い投資機会ということになる。
しかしながら、CAPMが証券の価格変動の全てを説明できるわけではないことには留意すべきだ。
投資家がとある企業がユニークで高い収益性をもたらす新製品の上市が予定されている企業の株式をCAPMのフレームワークでは割高となっても買い進むかもしれない。
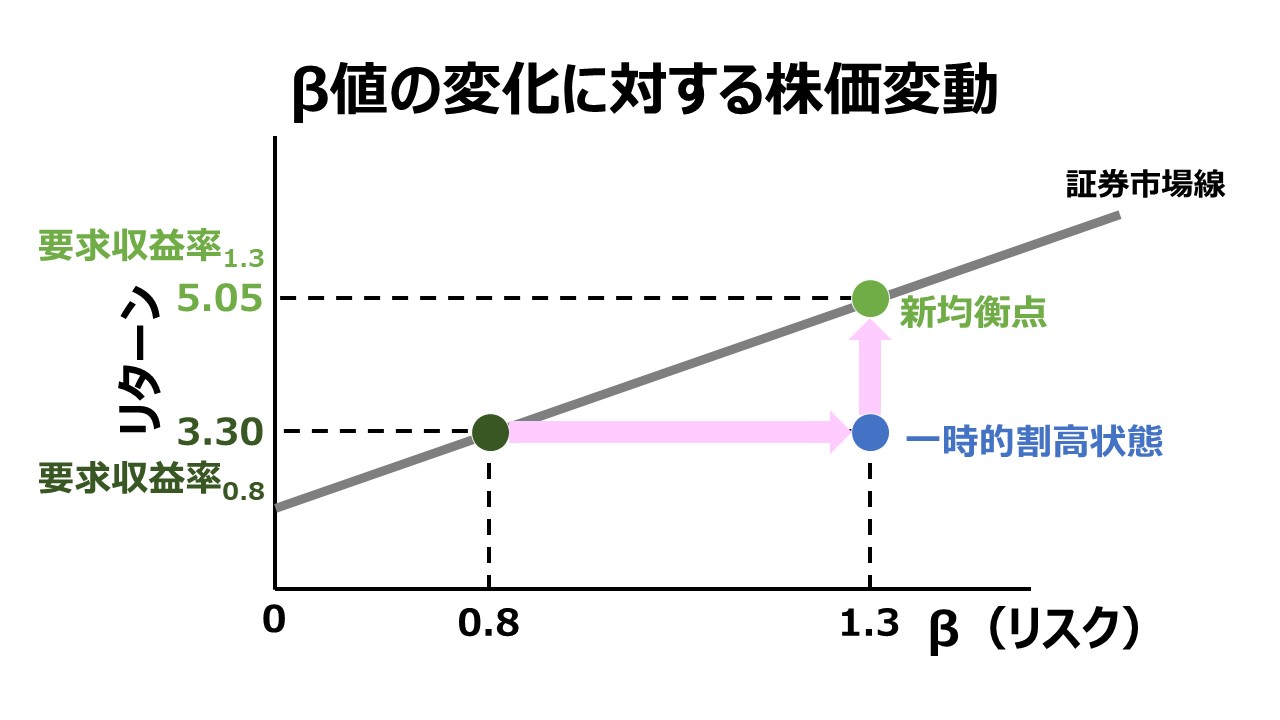
やがて、その高収益性が高い企業成長と収益性の向上を実際にもたらし、結果として増配がもたらされるとともに株価が大幅に見直されて、CAPMのフレームワーク内で新たな均衡点を証券市場線の上で実現することになる。
コメント