DCF法による企業価値評価の計算要素
要求収益率 Required Rate of Return
将来キャッシュフローの現在価値を計算する際に使用される割引率は、要求収益率(required rate of return)として知られている。企業は通常、投資家としての要求収益率を上回る収益が見込める場合にのみ己の資金を投資に向ける。
このように、その収益率は、市場が期待する収益率(期待収益率:expected rate of return)に個々の投資案件が投資に値するだけのリスクプレミアム(risk premium)を加えたものである。
割引率として用いられる要求収益率は、買収対象企業のキャッシュフローのリスクを反映するために、その企業の株式コストとなる必要がある。
買収しようとする企業の株式コストは、資本資産価格モデル(CAPM)を使って推計することができる。CAPMは、投資家からの要求収益率を決める手段である。CAPMを用いることで、リスクフリーレートにその企業の株式が直面するシステマティックリスク(分散不能リスク)に対応した上積み分を加味して、その企業の株式の最終的な要求収益率を計算することができる。
システマティックリスクが大きくなればなるほど、証券投資に投資家が望む要求収益率はより高くなる。
とりあえず、CAPMの計算式は次のように表すことができる。
\( \displaystyle \bf R=R_F+β(R_M-R_F) \)
- R: 投資家の必要利益率(目標利益率)
- RF:リスクフリーレート
- β: β値(その企業の株式の変動性(volatility)と市場全体の変動性の相対的な比較したもの)
- RM: 市場全体の期待収益率
- RM – RF: 市場のリスクプレミアム
- β(RM – RF): その企業の株式のリスクプレミアム
期待成長率 Expected Growth Rate
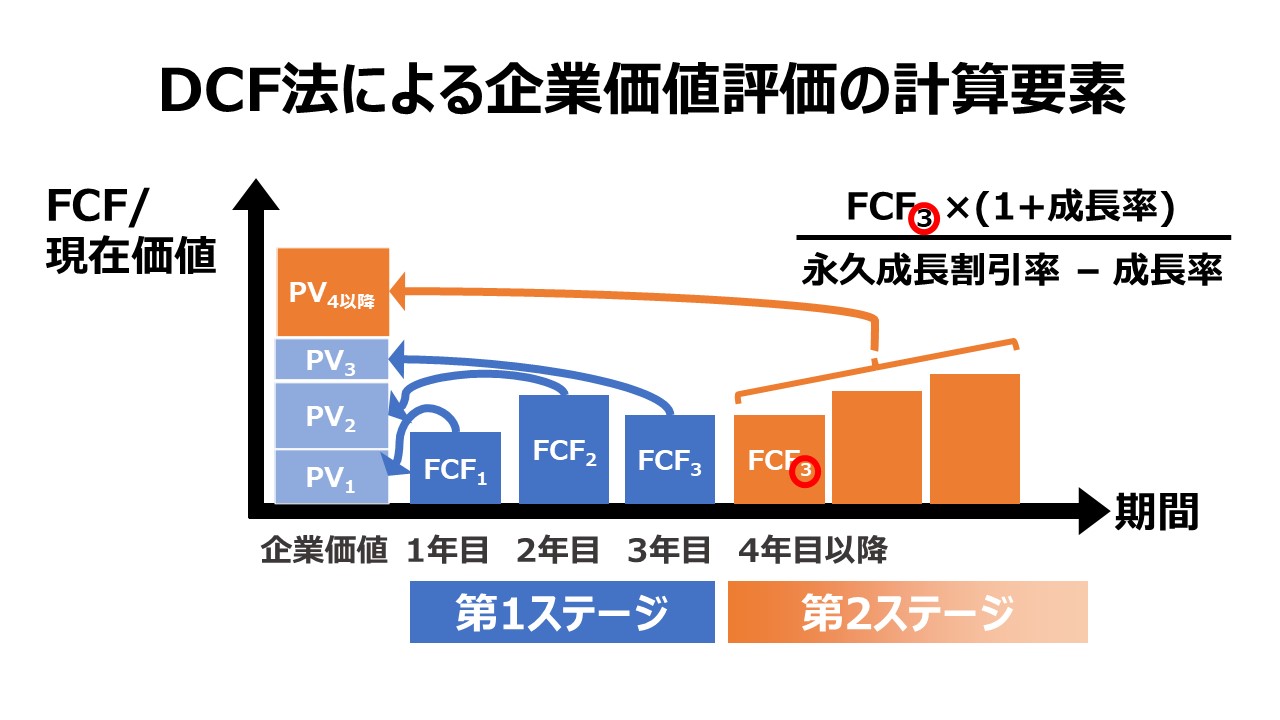
企業価値評価において、将来キャッシュフローの割引現在価値を算定する際に、二段階成長配当割引モデルのように、アナリストは2つのステージに分けて将来キャッシュフローを予測することが多い。
最初のステージは、将来のある特定の年限まで、財務諸表の細かい数値を分析して毎年のキャッシュフローを予測する。次のステージは、最初のステージの翌年から永遠に、ある定率の成長率でキャッシュフローが成長し続けるという仮定をおいて計算する。
このように、2つのパートから成る期待される将来キャッシュフローの割引現在価値を求めることで、その企業の本質的価値(intrinsic value)を推計しようとするものである。
最初のステージにおけるキャッシュフローの割引現在価値を求める計算は比較的シンプルである。しかし、次のステージにおける将来キャッシュフローの割引現在価値を求めるには、永久債のような永続性(perpetuity)を埋め込んだ計算をする必要がある。
定率成長率の世界では計算上、キャッシュフローは永遠に続くものだとしても、期待成長率を仮定してひとつ決めれば、計算結果はやがて収束して、そのキャッシュフローの割引現在価値は求めることができる。
一定の成長率で伸びるキャッシュフローの割引現在価値は、年率の成長率の多寡で決まるので、このモデルで最も重要なのは、この定率の期待成長率をはじく部分である。
ある将来時点を超えた先(ここでは便宜的に”次年度”と呼ぶ)の永久成長の将来キャッシュフローの割引現在価値を決める計算式は、Gordon Growth Model と呼ばれ、定率成長配当割引モデル(Dividend Growth Model)として、理論株価を算出する計算モデルと本質的には同じものである。
\( \displaystyle \bf 永続成長CFの割引現在価値 = \frac{次年度の期待フリーキャッシュフロー}{(資本コスト – 期待成長率)~~~~~} \)
期待成長率の求め方
期待成長率を実際に計算する場合には、持続可能成長率(Sustainable Growth Rate)の計算プロセスを踏襲することになる。
- 再投資比率を計算する
- 投下資本収益率を計算する
- 再投資比率×投下資本収益率=期待成長率を求める
長期におけるフリーキャッシュフロー(FCF)の成長は、各年度ごとに稼いだ利益を次の成長投資に回すことで実現されることから、FCFの成長は利益の成長からもたらされる。
ここで想定されるロジックの流れは次の通り。
❶今期利益を計上する → ❷来期のために稼いだ利益から幾分かを内部留保に回す → ❸内部留保を成長投資に使ってさらに利益額を増やす → ❹利益が増えるとフリーキャッシュフローも増える
この利益(内部留保)に対して次の成長投資に回される金額の比率を再投資率(plowback ratio)と呼ぶ。
長期的には、各年度の当期純利益から配当などによる社外流出から免れた金額、すなわち内部留保額と、企業の成長投資にかけるための再投資額は理論的に一致するため、再投資率=内部留保率(Retention Ratio) であると記述されていることも多い。
しかし、短期的には、前年度に内部留保された金額と、今年度に成長投資にかける金額は実務的にはいくらかずれることが多いため、計算に用いる数値と名称の取り扱いには注意しておきたいところである。
ここでは少しだけ横道に逸れるが、利益ベースでフリーキャッシュフロー(FCF)の成長率を簡便的に求める場合は、次の計算式が頭に入っていると計算のコツが理解しやすくなるかもしれない。
\( \displaystyle \bf 内部留保率(\%)=1–配当性向(\%) \)
例えば、配当性向(payback ratio)が40%ならば、再投資率(=内部留保率) は、1-40%=60% と計算することができる。
内部留保の再投資率の計算 Calculation of Rate of Reinvestment of Earnings
フリーキャッシュフロー自体は制度会計で開示されるべき項目とされていないため、直接的に財務諸表から示されるものではないうえ、その成長率をさらに求めようとするにはいくらかの工夫と努力が一層必要になる。
※ フリーキャッシュフローの定義にはいろいろあるが、有名どころには2つあって、ひとつは、シンプルに、営業活動によるキャッシュフローと投資活動によるキャッシュフローの単純合計とする手法である。これを、仮に❶制度会計準拠法(米国法)と名付けておく。もうひとつは、以下で説明する ❷管理会計法 である。いずれにせよ、単純に制度会計で開示されるべきものではない。
フリーキャッシュフロー(FCF)の再投資率の計算式を組み立てるための理屈を考える
ここでは、いくつかの仮定をおいて、間接的にフリーキャッシュフロー(FCF)の再投資率を求めることにする。
❶フリーキャッシュフロー(FCF)の再投資率が知りたい
❷長期的に見れば、当期純利益から内部留保に回った金額が企業成長に投資されることでFCFが増加するから、
→ ❸FCFと当期純利益の増減は比例的な関係にあると思われる かつ
→ ❹内部留保額と企業成長への投資額は、比例的な関係にあると思われる
→ ❺内部留保率(= 1- 配当性向) が常に一定ならば、当期純利益と内部留保額とは比例的な関係にあると思われる
❻限界税率:t が常に一定であるならば、当期純利益とEBITとは何らかの比例的な関係にあるはず
∵ 当期純利益 = (1 – t) × EBIT ± その他収支
→ ❼ならば、FCFとEBITも何らかの比例的な関係にあるはず
よって、
❸と❺より、FCFの再投資率には、当期純利益に対する再投資率の計算式が援用できるはずだし、
❼から、FCFの再投資率は、EBITを使って表現することもできるはず
フリーキャッシュフロー(FCF)の再投資率の計算式を組み立てる
管理会計法に基づくフリーキャッシュフロー(FCF)の定義式は、限界税率=t とすると、
\( \displaystyle \bf FCF =(1 – t)EBIT -(資本的支出-減価償却費)±運転資本増減 ・・・(1)\)
である。
これを、前章で確認した理屈により、当期純利益に対する再投資率の計算式の形にEBITを用いて、FCFの再投資率の計算式に再構成する。
(1)式の左辺第1項と右辺第2・3項を入れ替えた上で左右ひっくり返して、両辺を(1-t)EBITで割ると(既に答えを知っているからこそできる変形なのだが)、
\( \displaystyle \bf \frac{(1-t)EBIT-FCF}{(1-t)EBIT} = \frac{(資本的支出-減価償却費)±運転資本増減~~~~~~~~~~~~~~~~~~~~}{(1-t)EBIT} ・・・(2)\)
という形になる。
左辺を見ると、(1-t)EBIT というNOPAT的な利益概念からFCFを控除した値を(1-t)EBIT という NOPAT的利益概念で割り算している。これは、NOPAT的利益概念に基づく再投資率を表す式であると考えることができる。
FCFは、その事業から得られた付加価値であり、生産性分析における付加価値の分配論によれば、社外流出に相当する金額であるから、(2)の右辺は、FCFを用いたNOPAT的利益概念に基づく再投資率の内容を表すことになる。
(言い換えると、(1-t)EBIT-FCF の値は、内部留保額を意味する)
(2)式の左辺を概念(言葉)に置き換えて書き直すと、
\( \displaystyle \bf 再投資率 = \frac{(資本的支出-減価償却費)±運転資本増減~~~~~~~~~~~~~~~~~~~~}{(1-t)EBIT} ・・・(3)\)
※ 重ねてコメントするが、(3)式は、予め、管理会計方式によるFCFの定義式を知っていることと、FCFと当期純利益における再投資率の関係が比例的であるという知識とを前提にしないと、いきなりこれを導き出すことは大変難しい。初学者には(3)式をまず鵜呑みにして、使い込みながらじっくり理解していく方法をお勧めする
投下資本収益率の計算 Calculation of Rate of Return on Capital Invested
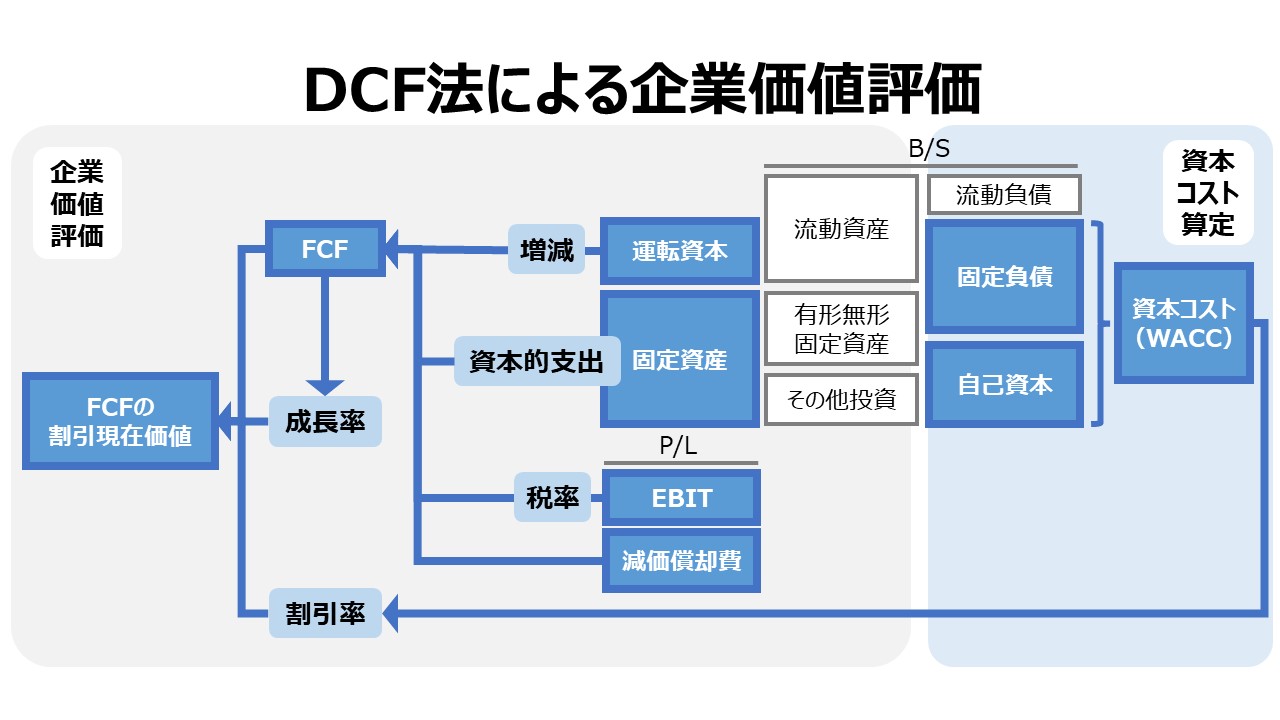
B/Sの金額をベースに資本収益率(資本利益率、資産収益率、資産利益率)を計算するものとして、ROI、ROA、ROE、ROICなどがある。
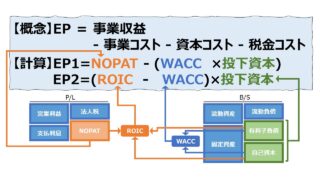
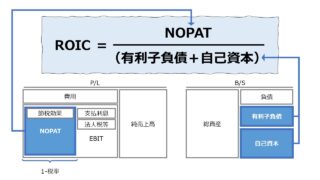
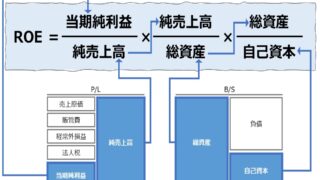
ここでは、フリーキャッシュフロー(FCF)を生み出す資産・資本の形として何が優れているかをまず考える。
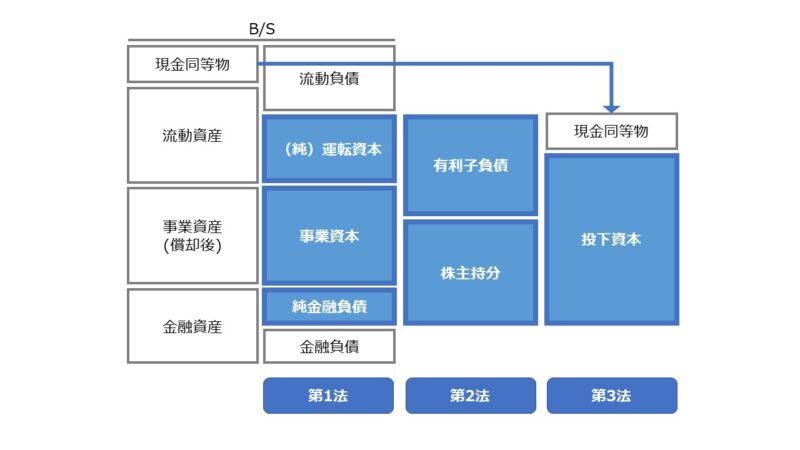
数ある教科書の中には、ROAと同様に、FCFの再投資率や資本収益率を計算するのに総資産を用いると解説しているものも存在する。
しかし、管理会計法によるフリーキャッシュフロー(FCF)の定義式は、運転資本増減を加味するようになっているため、上図(投下資本の計算方法)にある通り、「第1法」がふさわしいと思われる。
\( \displaystyle \bf 投下資本収益率 = \frac{(1-t)EBIT}{投下資本} ・・・(4) \)
期待成長率の計算 Calculation of Expected Growth Rate
期待成長率を計算する際に注意すべきなのは、再投資率も投下資本収益率も過去実績ではなく、将来予測値を用いることである。
それを理解し、実際に使いこなす(実際に数値を作る)ことの方が難しく、期待成長率自体を計算する式は至ってシンプルである。
計算式自体は、 持続可能成長率(Sustainable Growth Rate)と全く同じである。
\( \displaystyle \bf 期待成長率 = 再投資率 \times 投下資本収益率・・・(5) \)
具体的に実際数値を使って計算するには、(3)式と(4)式を(5)式にシンプルに代入すればよい。
\( \displaystyle \bf 期待成長率 = \frac{(資本的支出-減価償却費)±運転資本増減~~~~~~~~~~~~~~~~~~~~}{(1-t)EBIT} \times \frac{(1-t)EBIT}{投下資本} \)
\( \displaystyle \bf = \frac{(資本的支出-減価償却費)±運転資本増減~~~~~~~~~~~~~~~~~~~~}{投下資本} \)
資本コストの計算 Calculation of Cost of Capital
企業価値評価における資本コストは、CAPMを活用して、潜在的な買収先の企業の株式に対する要求収益率として立ち現れてくる。
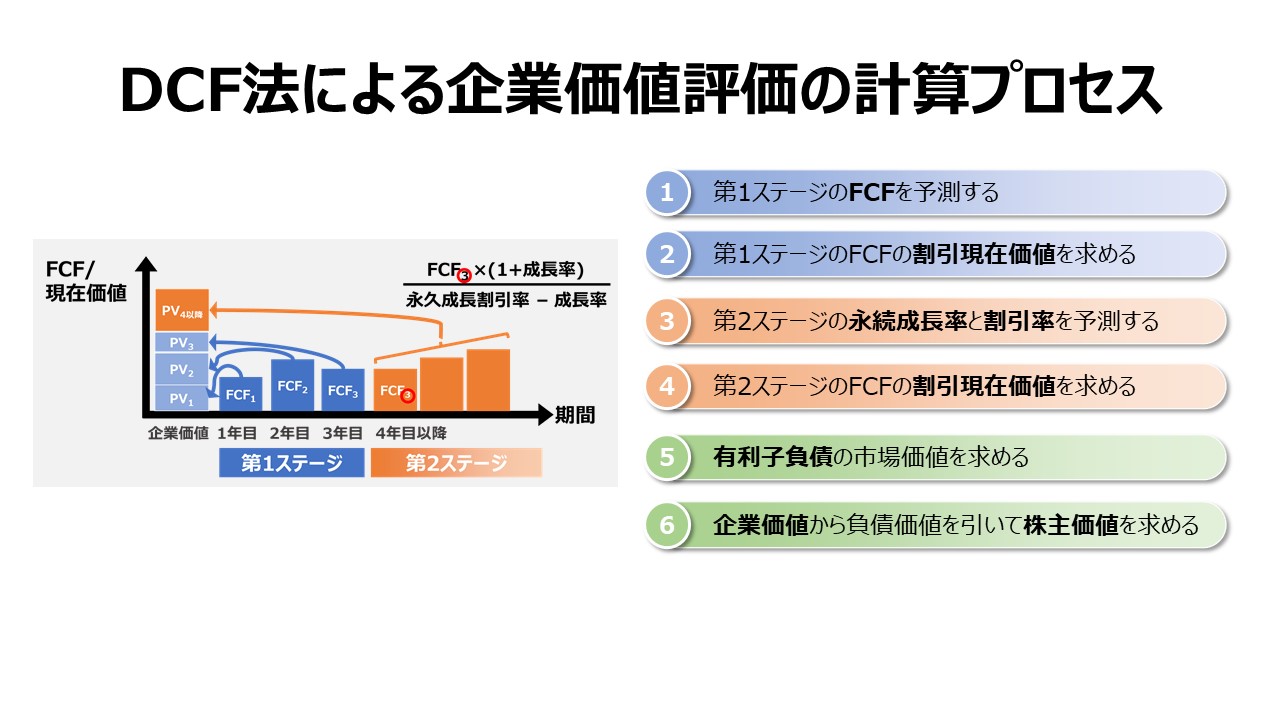
\( \displaystyle \bf FCFの割引現在価値 = 第1ステージのFCFの割引現在価値 + 第2ステージのFCFの割引現在価値 \)
例えば、定義式をシンプルにするために、第1ステージを3年と仮定し、割引率を10%とすると、
\( \displaystyle \bf 第1ステージのFCFの割引現在価値 = \frac{FCF_1}{(1+10\%)^1}+\frac{FCF_2}{(1+10\%)^2}+\frac{FCF_3}{(1+10\%)^3} \)
例えば、 定義式をシンプルにするために、第2ステージが4年目にスタートすると仮定し、割引率を15%(実務的には第1ステージの割引率と変える/変えないは大きな問題だが敢えて違える)とし、成長率を12%とすると、
\( \displaystyle \bf 第2ステージのFCFの3年度末時点の割引現在価値 = \frac{FCF_{3} \times (1+12\%)}{15\% – 12\%} \)
この値を、第1ステージと同じ時点に揃えるために、1年目が始まる前の時点まで割り引いてくると、
\( \displaystyle \bf 第2ステージの割引現在価値 = \frac{第2ステージのFCFの3年度末時点の割引現在価値}{(1+10\%)^3} \)
上記を分割したまま頭の中で足し座して理解すればよいが、FCFの割引現在価値を PVFCFと表記し直し、一応この画面上で合わせて記述することを試みると、
\( \displaystyle \bf PV_{FCF} = \frac{FCF_1}{(1+10\%)^1}+\frac{FCF_2}{(1+10\%)^2}+\frac{FCF_3}{(1+10\%)^3} + \frac{\left(\frac{FCF_{3} \times (1+12\%)}{15\% – 12\%}\right)}{(1+10\%)^3} \)
注意すべき点は、第2ステージの始まりのFCFの値を、第1ステージの最終年度のFCFに成長率を乗じたものを使うか、改めて第2ステージの始まりのFCFの値を定義し直した方がよいかを見極めることである。
もちろん、計算モデルの一貫性とシンプルさからは、前者の方をお勧めはする(上記の例も前者に倣っている)。
コメント