β値の変化に対する株価変動
概要
β値は個々の証券投資(個別株式、投資ポートフォリオ)のシステマティック・リスクを表すものである。そしてこのシステマティック・リスクが個々の証券投資のリターン(要求収益率)を規定する。
システマティック・リスクが高くなればなるほど、β値がより大きくなる。β値がより大きくなるほど、投資家がその証券投資を続けるのに必要と考えるリターン(要求収益率)が高くなる。
したがって、証券の市場価格は投資家がその証券を保有する際に感じるリスク量に影響を受けることになる。もし投資家がよりリスクが高くなると考えるならば、そのリスクを中和・相殺するためにもっと高いリターンが必要になる。高いリターンを実現するには、その証券の市場価格を下げることになる。
例証
β値が0.8の株式Aがあると仮定する。投資家が期待している市場全体のリターンが4%でリスクフリーレートが0.5%だとすると、CAPMに基づく株式Aの要求収益率Rは、
\( \displaystyle \bf R=リスクフリーレート+ β(市場全体の期待収益率-リスクフリーレート) \)
\( \displaystyle \bf =0.005+ 0.8(0.04-0.005) =0.005+0.028=3.3\% \)
株式Aの要求収益率が3.3%と、市場全体の期待収益率の4%を下回っているのは、株式Aのβが0.8と1を下回っているからである。
(※ よりリスクが小さい(=価格変動が少ない)投資機会に対する要求収益率はより低く抑えられるため)
ここで、株式Aが、積極的なデッドファイナンスによる規模の拡大を図ったとする。株式Aに対面する投資家の心理として、株式Aがより大きな収益をもたらす可能性が膨らむものの、よりリスクも大きくなると感じるため、市場全体との相対比較により、以前より株式Aの価格変動(volatility)が大きくなることを予想するはずだ。
この投資家からの株式Aに対するリスク評価の変化を、β値の0.8から1.3への変化分として定量化できると仮定したなら、CAPMに基づくと、株式Aの要求収益率Rは、
\( \displaystyle \bf R=0.005+ 1.3(0.04-0.005) =0.005+0.045=5.05\% \)
となる。
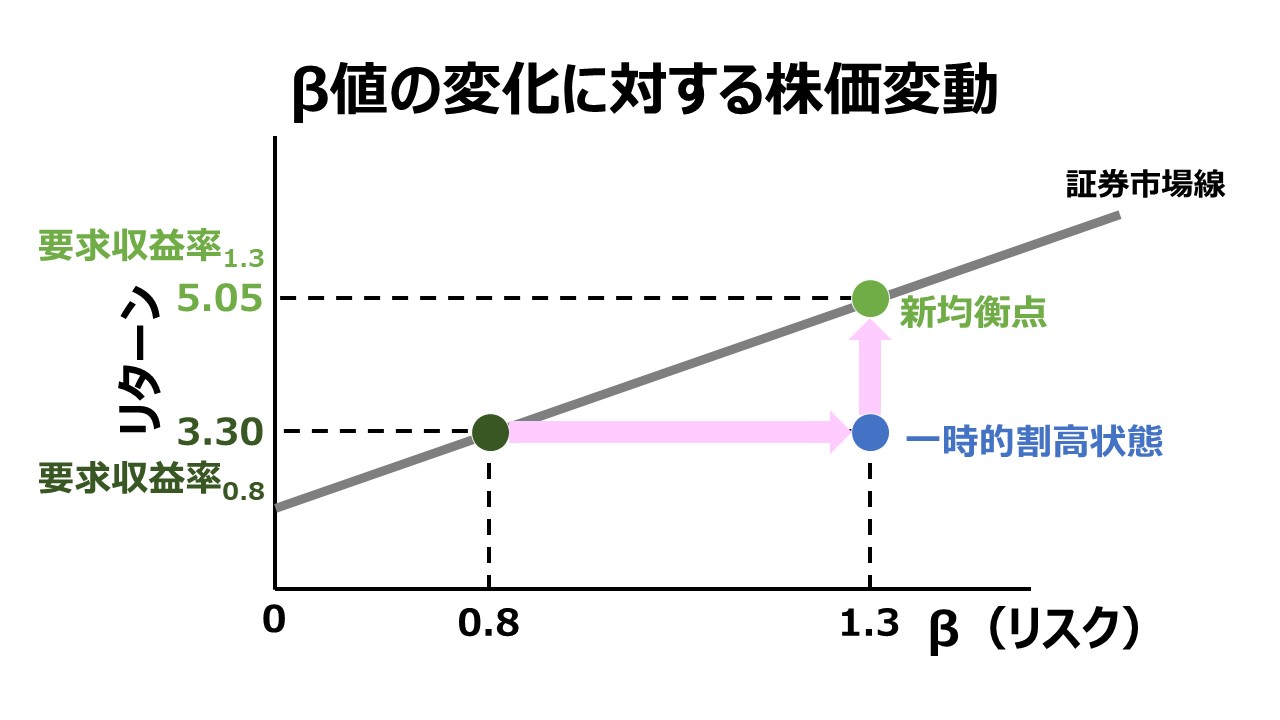
株式Aに対する投資家からの要求収益率が3.3%でβ値が0.8から要求収益率5.05%でβ1.3まで増進することで、株式Aは再び証券市場線(SML)上に戻ってくるのである。
投資家は、株式Aのリスクと収益率がどちらも増進することを予期し、株式Aを保有し続けるためには(新規で買いを入れるには)、従来より高い期待収益率が実現されることでしか惹きつけられないのである。
リスクプレミアム
投資家に対してβが1.3の水準で株式Aの継続保有・新規購入に動機づけるためには、株式Aのリスクプレミアム(risk premium)が、1.3 × (0.04 – 0.005) = 4.55% まで必要である。
以前は、株式Aのリスクプレミアムは、 0.8 × (0.04 – 0.005) = 2.8% しか必要ではなかった。
このリスクプレミアムの上昇は、ひとえに株式Aのシステマティック・リスクが増大したからである。
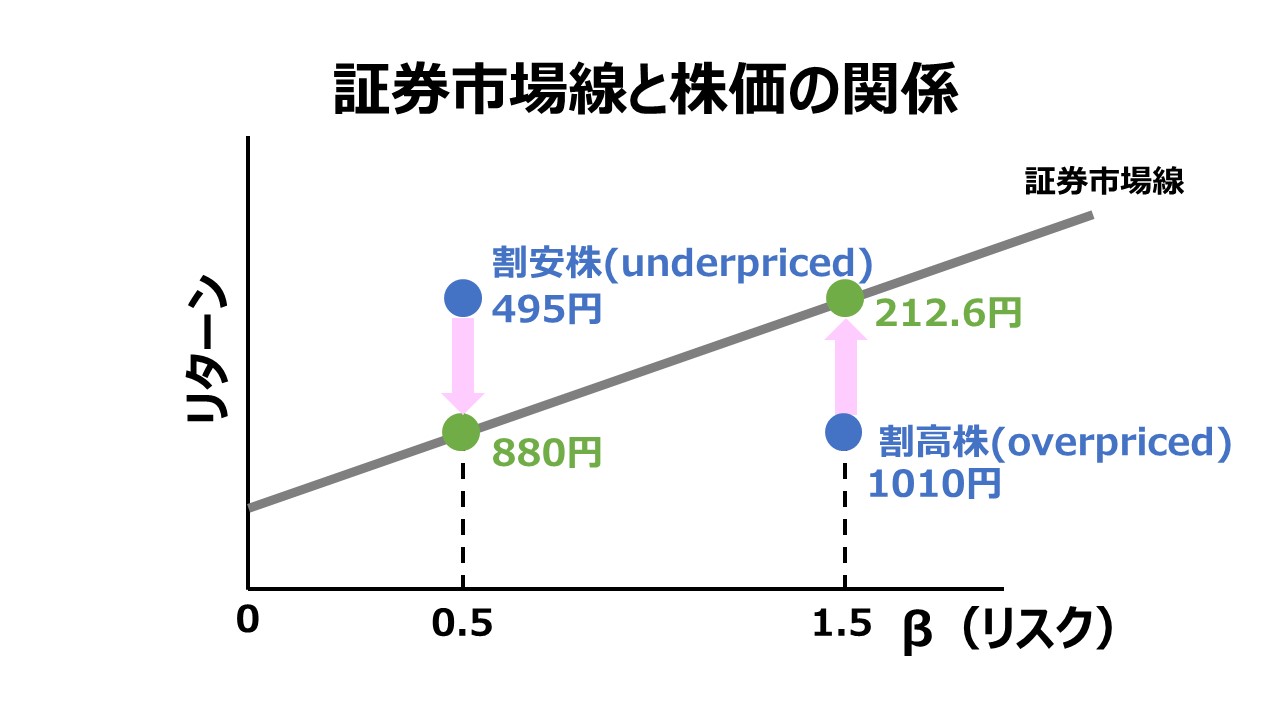
ひとたび投資家からの(市場からの)要求収益率が異なれば、市場における実際株価は変動する。高いリスクに対応するために、他の投資家が株式Aを保有したいと感じる水準に期待収益率を下げる(要求収益率=期待収益率を実現する)まで、株式Aの実際株価は下落するのである。
コメント