投資ポートフォリオのリスクとリターン Portfolio Risk and Return
投資ポートフォリオはグループとして管理された資産の集合体で、個々の投資家にとっては、多様な株式やその他の市場性有価証券をひとつの投資ポートフォリオとして扱うことができる。
ポートフォリオ理論 Portfolio Theory
ポートフォリオ理論は、リスクとリターンに配慮した投資家の選好に従って最適な投資ポートフォリオを構築することを目指す投資哲学である。
ポートフォリオ理論によれば、個々の証券はそれ単独の投資(standalone)として評価されることはない。その代わり、それぞれの証券の市場価値は投資ポートフォリオの内部でその他の証券の市場価値との相関関係で評価される。
与件とされた投資家のリスク選好水準に従って、投資ポートフォリオはリスクに見合った期待収益率を最大にするように構築されることになる。あるいは、与件とされた投資家の期待収益率のレベルに従って、投資ポートフォリオは期待収益率に見合ったリスクを最小化するように構築されることになる。
キーとなるのは、投資ポートフォリオは分散投資(diversification)されることである。分散投資の概念は、リスクを減少させるような証券を組み合わせることである。多種多様の金融商品を組み合わせることで、市場価格の変動の方向性を正反対に向かせるようにすることができる。
ある金融商品の市場価値が減少すると同時に、別の金融商品の市場価値が増大することで損失を相殺することが可能になる。例えば、景気循環株(cyclical)への投資をディフェンシブ株への投資と組み合わせることである。
分散投資は、多種多様の証券投資を組み合わせることで、たった一つの証券投資が引き起こす損失による投資ポートフォリオ全体に及ぼす影響を最小限に食い止めることができる。
投資ポートフォリオにおけるリスク削減は、お互いに相関関係を持たないか、ある以下相関関係ができるだけ小さいものを組み合わせることで可能になる。分散投資は、決められた期待収益率の中でリスクを最小限にし、あるいは、決められたリスクの中で期待収益率を最大化にしてくれる。
資産配分(asset allocation)は、投資ポートフォリオの中で、最良のリスク・リターンのトレードオフの状態を実現するために多種多様の金融商品を組み合わせて、選び出すプロセスそのものである。
選ばれる資産には、債券、株式、不動産の他、ハイイールド、ローリスク、長期、短期の各種投資が含まれる。それらの組み合わせとして、すべてリスクとリターンの正しい組み合わせを実現するためのものが選ばれる。
十分な数の金融商品への投資とは、分散投資によるベネフィットを十分に引き出すことができるだけのバリエーションを有する投資である。そうした分散投資は、特に、「完全な分散投資(fully diversified)」とか「効率的な投資ポートフォリオ(efficient portfolio)」という風に呼ばれる。
そうした投資ポートフォリオによる分散投資は、特定のリスクの中で最高のリターンを稼ぎ出すし、特定のリターンの中で最小のリスクを実現するものではあるが、それは必ずしも完全にリスクをなくすことを意味はしない。ある特定のリターンを享受するには、それなりの最小限に抑制されたリスクも受ける覚悟を必要とする。
個々の金融商品が有するリスクは分散投資により軽減できるものであり、分散可能リスク(diversifiable risk)、アンシステマティック・リスク(unsystematic risk)、非市場性リスク(non-market risk)と呼ばれるものである。
非市場性リスクは、個々の金融商品固有のものだから、市場全体には全く影響せずに削減することができるものである。例えば、労働ストライキ、工場火災、コンペチターが有する特許権、技術革新による既存製品の陳腐化などが挙げられる。
特定の種類のリスクは分散化でも減少させることはできない(より厳密な表現をするなら分散化することはできない)。市場リスク(market risk)やシステマチックリスク(systematic risk)は分散化で回避することはかなわず、分散不能リスクとして残り続ける。
すべての金融商品は好不況の波による経済環境の変化から免れることはできない。景気変動は全ての経済的主体に影響を及ぼし得るし、公的年金資金によるファンド等は、景気が悪化したからといって急に投資を中断することはできない。
また、ある程度の分散されつくされていないことにより発生するリスク、損益によるダメージ(損失)を相殺(offset)するために組み合わされる金融商品同士の不完全な相関関係が引き起こすリスクが存在する。
資産配分 asset allocation
ポートフォリオ理論は、リスクとリターンのバランスを扱うもので、投資ポートフォリオに相応しい金融周品の選別も取り扱うものである。投資ポートフォリオは、適切な資産配分(asset allocation)を通じて管理されるものである。
結果として、投資ポートフォリオに含まれる個々の金融商品のリスクより、投資ポートフォリオ全体のリスクは、小さくなるのが普通であり、少なくとも個々の金融商品のリスクの単純合計よりも小さくなるはずである。
| リスク | 金融商品 | 英語名称 |
|---|---|---|
| リスク最小 | 国債 | Treasury Bonds |
| ↑ | 一番抵当証券 | First Morgage Bonds |
| ↑ | 二番抵当証券 | Second Morgage Bonds |
| ↑ | 劣後債 | Subordinated Deventures |
| ↓ | 毎年支払金確定保証債券 | Income Bonds |
| ↓ | 優先株式 | Preferred Stock |
| ↓ | 転換権付き優先株式 | Convertible Preferred Stock |
| リスク最大 | 普通株式 | Common Stock |
ポートフォリオ理論における相関係数
一般的に、相関係数(coefficient of correlation)は、二つの変数の関係を定量化したものだ。相関係数の大きさは二つの変数の連動性や関係性がどれだけ近いか(遠いか)を表す。
その定量化の根拠として、通常は過去の時系列における統計的データ(histrical data)を用いたものが計算されて使用される。より厳密にいえば、共分散(covariance)を求めることになる。共分散の値を、各変数の標準偏差の積で割ったものが相関係数となる。
相関係数は一般的に”R”、”r”で表され、プラスマイナスの符号と、0から1の間の数字を用いる。実際には、-1 ≦ R ≦ +1 で表される。
以下では、二つの変数を2銘柄の株価として説明する。
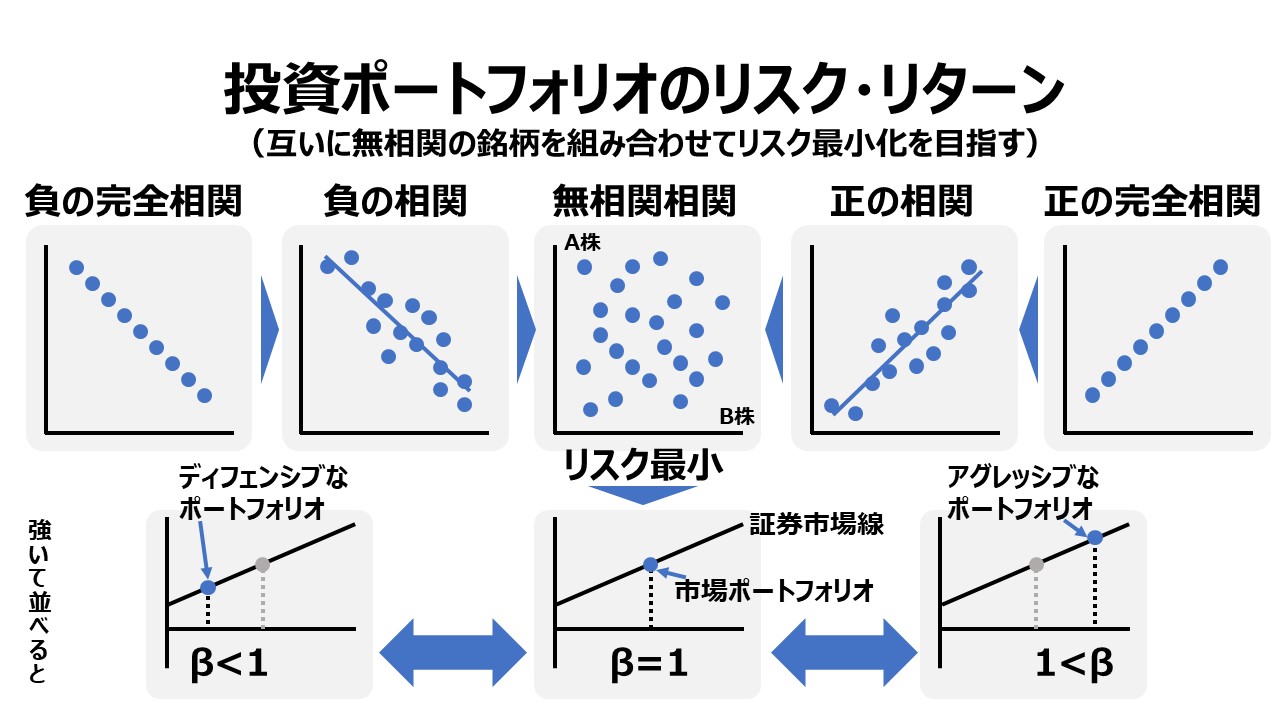
R = +1 正の完全相関
一方の株価が上昇すれば同じ比率でもう片方の株価も上昇し、一方の株価が下落すれば、同じ比率でもう片方の株価も下落する関係にある。いわゆる直線的(liner)な関係で、散布図に表すと、右肩上がりの直線になる。
0 < R < +1 正の相関
一方の株価が上昇すればもう片方の株価も上昇するが、上昇する比率が異なる。一方の株価が下落すれば、異なる比率ではあるが同様にもう片方の株価も下落する。散布図に表すと、右肩上がりの分布になる。
R = 0 無相関
特に2つの銘柄の株価変動に関連性がみられない。投資ポートフォリオを構成するには、できるだけ無相関の銘柄を組み合わせれば、株価変動がお互いに相殺されることでリスクを減じることができる。
散布図を眺めても、点が不規則に散らばるだけで、見た目で何か特別なインサイトが得られるわけではない。
0 < R < +1 負の相関
一方の株価が上昇すればもう片方の株価は逆に下落するが、変動する比率が異なる。一方の株価が下落すれば、異なる比率ではあるが同様にもう片方の株価は上昇する。散布図に表すと、右肩下がりの分布になる。
R = -1 負の完全相関
一方の株価が上昇すれば同じ比率でもう片方の株価が逆に下落し、一方の株価が下落すれば、同じ比率でもう片方の株価が上昇する関係にある。いわゆる直線的(liner)な関係で、散布図に表すと、右肩下がりの直線になる。
相関関係の強弱
一般的に、ピアソンの積率相関係数では、相関係数(R)が、
- 0 < R < 0.3:ほぼ無相関
- 0.3 ≦ R < 0.5:非常に弱い相関
- 0.5 ≦ R < 0.7:相関がある
- 0.7 ≦ R < 0.9:強い相関
- 0.9 ≦ R < 1:非常に強い相関
であると表現することがある。以上を表にまとめれば、
| 相関係数 | 区分 |
|---|---|
| R = 1 | 正の完全相関 |
| 0.9 ≦ R < 1 | 正の非常に強い相関 |
| 0.7 ≦ R < 0.9 | 正の強い相関 |
| 0.5 ≦ R < 0.7 | 正の相関がある |
| 0.3 ≦ R < 0.5 | 正の非常に弱い相関 |
| 0 < R < 0.3 | ほぼ無相関 |
| R = 0 | 無相関 |
| -0.3 < R < 0 | ほぼ無相関 |
| -0.5 < R ≦ -0.3 | 負の非常に弱い相関 |
| -0.7 < R ≦ -0.5 | 負の相関がある |
| -0.9 < R ≦ -0.7 | 負の強い相関 |
| -1 < R ≦ -0.9 | 負の非常に強い相関 |
| R = -1 | 負の完全相関 |

投資の世界には、厳密には数学的背景は従姉弟ぐらいの関係はあるが、定義が異なる数値(係数)がいろいろある。この相関係数とβ値(ベータ値)もその好例だ。
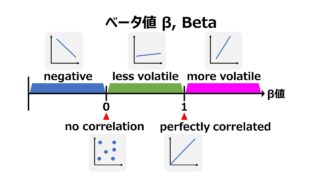
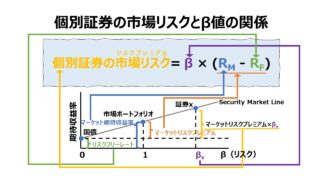
市場全体(日本の場合はTOPIXや日経平均等)と個別証券の値動きの連動性を表すのがβ値で、
β=1のとき、市場全体と個別証券の値動きは全く同じ連動を見せる。上記では、R=1、正の完全相関の場合と一致する。
β=-1のとき、市場全体と個別証券の値動きは全くの反対方向になる。上記では、R=-1、負の完全相関の場合と一致する。
β=0のとき、その個別証券は全く値動きをしない、リスクフリーの証券であることを意味する。
ここが重要で、相関係数がゼロということは、個々の証券の値動きが無相関ということだから、それは市場ポートフォリオを示すという理解になる。よって相関係数がゼロとβがゼロは意味が異なる。
-∞ < β < 0 は、一般的にネガティブベータとして、市場全体とは反対の値動きをするものだから、投資ポートフォリオを組む際には歓迎される銘柄となる。このような判定の際に、「-1」の上下にはあまり注目されない。程度の差として認識する。
0 < β < 1 のとき、その証券の値動きは市場全体に比べて緩慢になる。低ボラティリティ銘柄とか、ディフェンシブ銘柄と呼ばれて、ネガティブベータ銘柄より発生頻度が高いので、こちらも投資ポートフォリオを組む際には重宝される。
1< β < +∞ のとき、その証券の値動きは市場全体に比べてより激しいものになる。高ボラティリティ銘柄とか、景気敏感株(その類縁でcycrical銘柄とも)とか呼ばれる。いわゆるハイリスク・ハイリターンの株として扱われる。
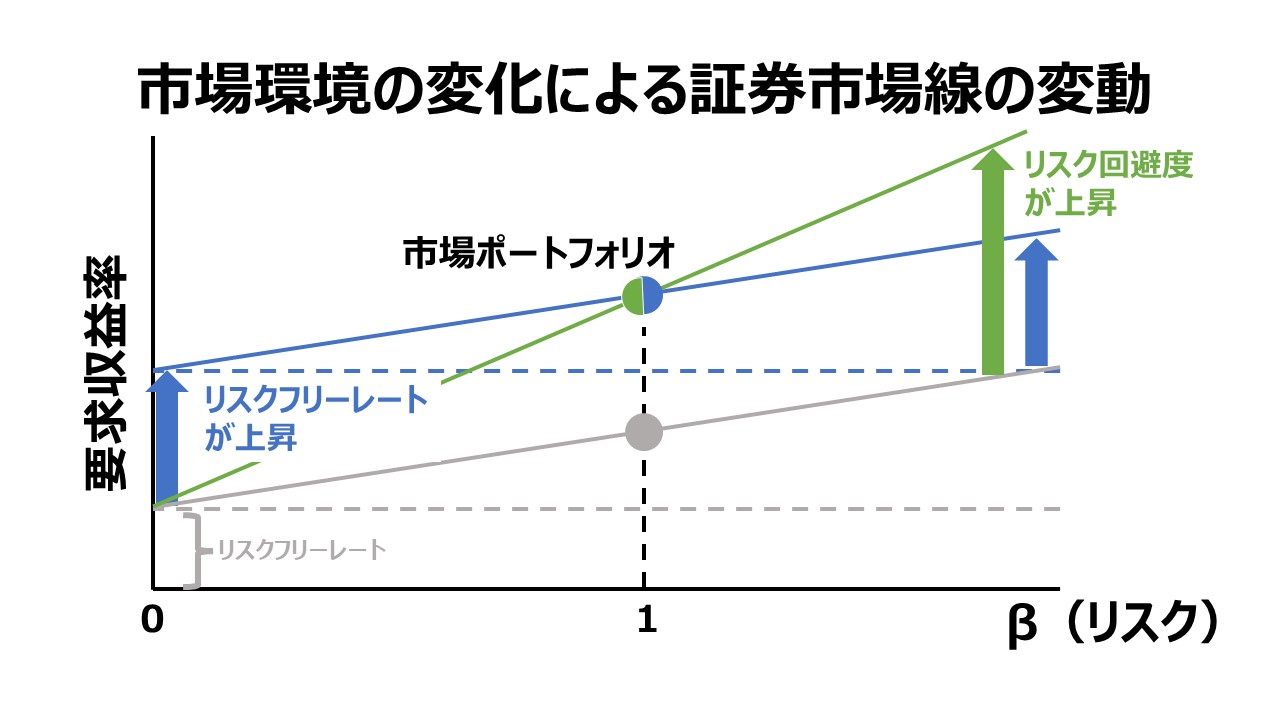
β値の解説でも触れたが、ネガティブベータや負の相関関係にある銘柄は、過去履歴が何かの特殊な原因で発生していると思われるため、将来にわたってずっとその負の相関が続く保証はないということは忘れてはいけない。
投資ポートフォリオを組む際には重宝するけれど、投資ポートフォリオの効率性を保つためには、定期的にチェック・再計算して、ネガティブ度(負の相関度)を常にウオッチして銘柄入れ替えに備えておく必要がある。
コメント