リスクフリーレート(RFR: Risk-Free Rate)
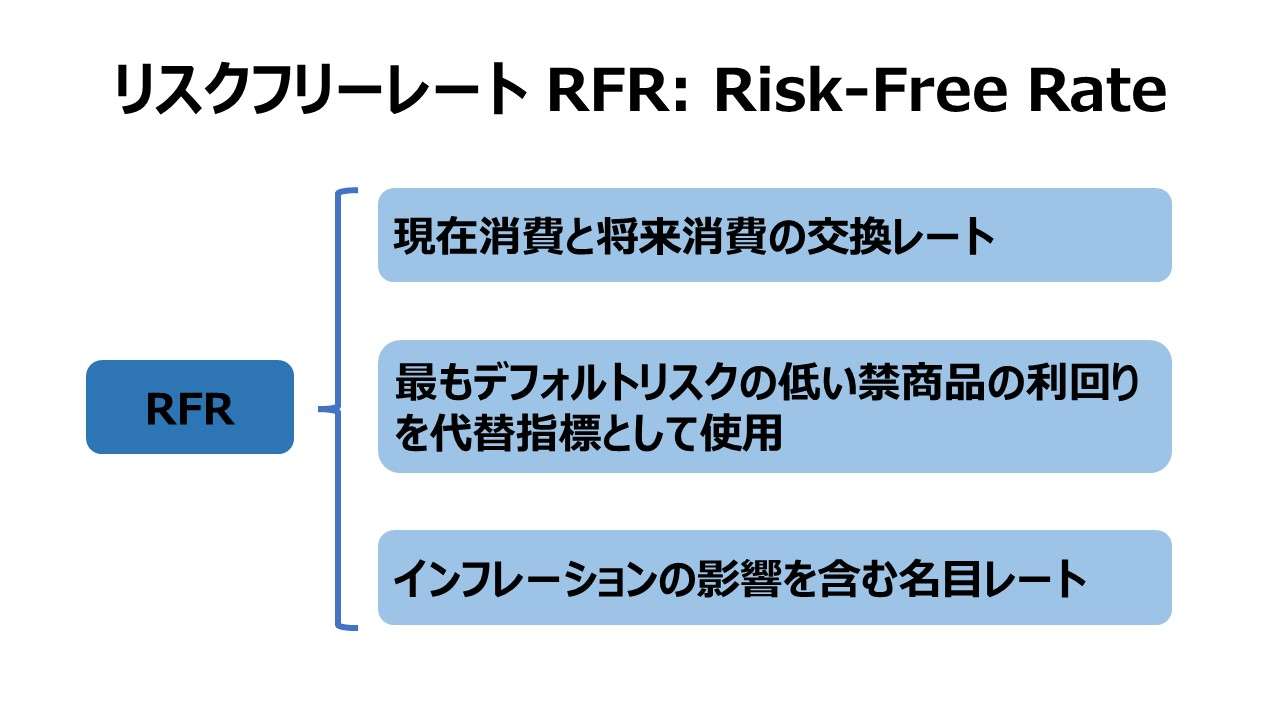
リスクフリーレートは、完全な安全資産に投資がなされたときの 貨幣の時間価値 (Time value of money) を表す純然に理論的なレート(金利)である。
消費者や投資家は、❶自分のお金を招来の資金ニーズのために貯蓄しておくより、直ぐに目の前の消費のために使う方を選好する、❷自分のお金を消費から貯蓄に回すためには、何らかの補償(compensation)を要求する、という理論に基づく。
この「補償(compensation)」の正体が金利である。
経済学者は、この消費選好を消費のための時間選好(time preference for consumption)と呼ぶ。
リスクフリーレートは、将来のとある時点でより多額の消費ができると期待する代わりに、現時点のお金の消費を諦めることに対して、投資家が要求するリターンを表している。
いわば、リスクフリーレートは、将来の消費がもたらす効用と現在の消費がもたらす効用の交換レートのように機能する。
この消費のための時間選好と、現在消費を諦めるための補償要求は、余剰資金の資本市場(金融市場)への供給に影響を及ぼす。
※ 余剰資金とは、投資家がすぐさま自分で消費する必要が無く、他人に貸し出したり、何かの金融商品に投資することができる待機資金(いわゆる貯金に回せるお金)のことを意味する。
資金の供給曲線と、資金の需要曲線の交点が、均衡点であるリスクフリーレートとなる。
※資金の需要は、とある経済的主体の資金ニーズであり、資金の赤字(deficit)を指す。赤字だから、他の経済的主体から不足しているお金を借りたいと考える。
例えば、国家の財政赤字(福祉政策のための支出)が増えると、政府による資金需要(国債発行での穴埋めニーズ)が高まる。
この時、貸し手からの十分な資金供給が無ければ、政府がその不足資金を穴埋めするために発行する国債の利率(金利)をもっと上げて不足資金を穴埋めしようとするはずだ。
国債の金利が上がれば、その他の公社債も、それまでの国債の金利とのバランスを維持するために、少なくとも同率以上に金利(利率)を上げざるを得ない。
実際には、銀行が公表する貸出金利の代表例としての「長・短期プライムレート」や、中央銀行が公表する「FFレート(フェデラル・ファンドレート)」のように、世の中に対して”リスクフリーレートは現在何%です” という明示的な指標が公開されるということはない。
※ FFレート:日本の無担保コール翌日物に該当
最良のリスクフリーレートの代理指標は、米国財務省短期証券(short term U.S. treasury bill rate)である。
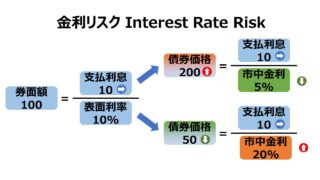
なぜなら、国際金融市場において、米国政府が債務不履行(デフォルト)のリスクが最も低いからである。そのことは、米国財務省短期証券を保有さえしておけば、それ以外のいかなる固定金利の金融証券を保有するより、投資家は最も金利リスク(interest-rate risk)から解放されるからである。
※金利リスク:世の中の金利変動により、投資した証券の現在価値が変動してしまうリスク
リスクフリーレートは、それ自体は名目金利(nominal rate of interest)である。”名目”の意味は、その数字に将来にわたっての予想インフレーションの影響度を加味しているということだ。
結局のところ、将来のとある時点での消費(により得られるより大きいと推測される効用)を諦めて、消費者が目先の消費(によって得ることができる効用)を選好するということは、インフレーションによって将来消費の幾分かを食い潰されてしまうことを望んではいないということを意味する。
この場合、消費者は、将来時点の消費量(から得られる効用)の増分が、インフレーションに打ち勝つことができないと考えていることになる。
ここから、次の式が理論的に成立すると考えられる。
●簡便法
実質リスクフリーレート = 名目リスクフリーレート – インフレーション
名目リスクフリーレート = 実質リスクフリーレート + インフレーション
上式はシンプルで頭に入りやすいが、実は数学的には厳密性に欠け、各レート(各金利)の絶対値が大きくなると、無視できないほどの誤差が発生する。
●原則法
\( \displaystyle \bf 実質リスクフリーレート = \frac{1+名目リスクフリーレート~~~~~~~~~~~~~~~}{1+インフレ率}-1 \)
簡便法に比べて計算式が複雑になるが、こちらは各変数の絶対値が大きくなっても誤差が発生しない。
しかし、実務上でリスクフリーレートを扱う際に、上式をそのまま使用することはあまりないだろう。
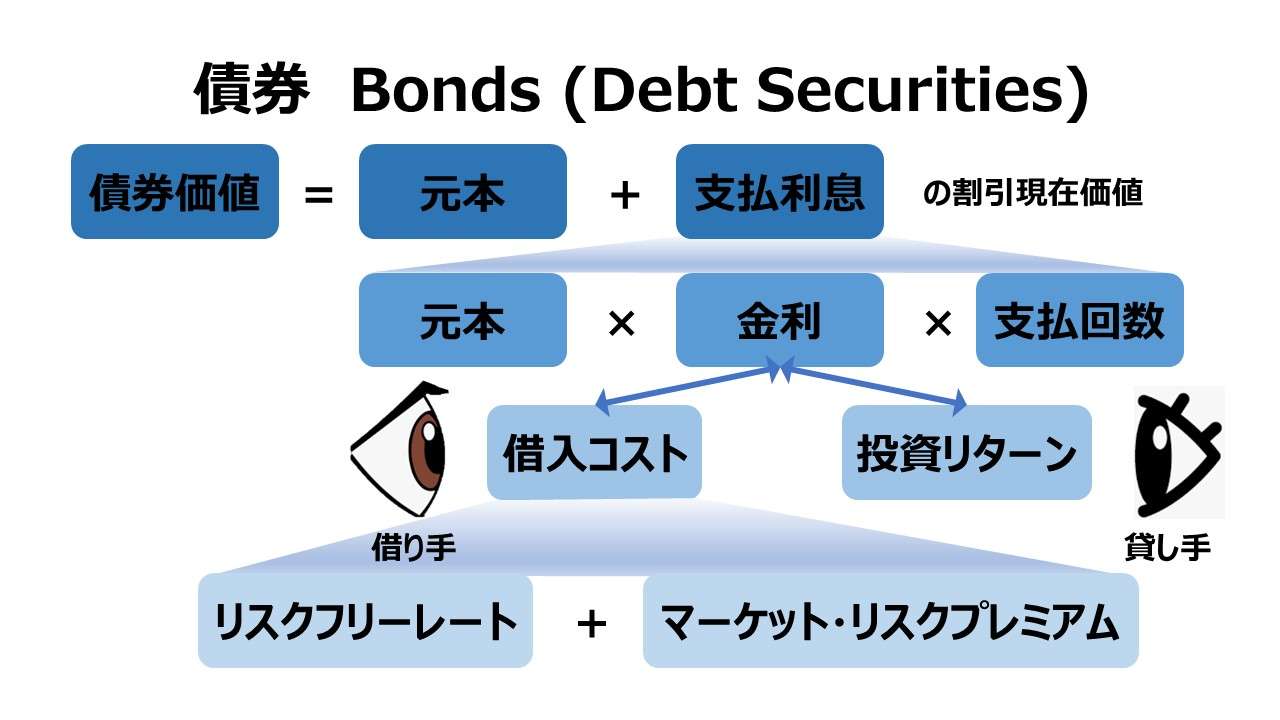
実際の金利は、このリスクフリーレートにマーケット・リスクプレミアム(Risk Premium)を加算したものとなる。
リスクフリーレートにマーケット・リスクプレミアムを加算した実際の金利を求めてから、その金利に対して名目レートか実質レートかを問うことがほとんどだからである。
あわせて読みたい



コメント