個別法（組み合わせ）で損益分岐点販売数量を求める – 複数セグメントのCVP分析

計算手法

個別法での損益分岐点販売数量の求め方

個別法が、複数セグメント間で販売構成比（セールスミックス）が一定（不変）ではないときに用いられる点については、こちらのリンクを参照

複数セグメントの組み合わせ次第で貢献利益の積み上げ額が変わる

個別法（組み合わせ）では、複数セグメントの貢献利益の積み上げ順序として考えられるすべての範囲を考慮して損益分岐点販売数量を求める。

全く同じセグメント構成でも、どのセグメントを優先して積み上げるかで、セグメントごとの貢献利益単価が異なれば、計算される損益分岐点販売数量も異なってくる。

それゆえ、個別法（組み合わせ）の計算方法において、損益分岐点販売数量は１点に定めることができず、範囲（バンド）で示されることになる。

例えば、企業内に下記のような2セグメントを有しているものとする。

項目	Aセグメント	Bセグメント
販売数量（個）	100	100
貢献利益単価（円）	@10	@50

固定費が 1500円 である場合、Aセグメント→Bセグメントの順か、それともBセグメント→Aセグメントの順序で貢献利益を積み上げていくかで、取り得る損益分岐点販売数量の値が変わってくる。

Aセグメントを優先して貢献利益を先に積み上げる場合、

となり、Aセグメント：100個、Bセグメント：10個、合計：110個が損益分岐点販売数量として求められる。

次に、Bセグメントを優先して貢献利益を積み上げていくとした場合、Bセグメント全体の貢献利益（5000円）が既に固定費発生総額（1500円）より大きいことが分かっているので、

となり、Aセグメントに属する商材の販売は一切必要とせずに、Bセグメントの販売可能数量100個のうち、30個の販売だけで、会社全体の損益分岐点販売数量に達することができる。

上例のような積み上げ順の選択で計算される損益分岐点販売数量が異なってくる理由は、各セグメントの貢献利益単価が異なるからに他ならない。

計算プロセス

個別法に特有のセグメントごとに考えられるだけの貢献利益の積み上げ優先順位の組み合わせに着目した損益分岐点販売数量の計算方式から、以下のシミュレーションプロセスが考えられる。

シミュレーション

Excelテンプレート形式で複数セグメントにおける個別法（組み合わせ）で損益分岐点販売数量を求める計算方法を示す。

入力欄の青字になっている「セグメント名称（任意の名前）」「販売数量」「販売単価」「変動費単価」「固定費」に任意の数字を入力すると、個別法（組み合わせ）に基づいた複数セグメントごとの損益分岐点販売数量が求められる。

但し、個別法（順列）で損益分岐点販売数量を求めるために、貢献利益の積み上げ順に左から入力するという制約は、個別法（組み合わせ）では不要となる。

どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。

自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。

テンプレートの使い方

販売数量

これから損益分岐点販売数量を求めるのに、あらかじめ各セグメントの「販売数量」を入力することが奇異に感じられる人がいるかもしれない。

この販売数量は、

❶実績販売数量で、過去実績を後から振り返って、損益分岐点販売数量を求めて次期以降の参考にする
❷予算/計画販売数量で、これから目標とする損益分岐点販売数量を設定するために計算する

という風に、どのタイミングでどんな目的でこのテンプレートを活用したいかで、使い分けができるようにできるだけ汎用的に製作されている。

グラフの見方

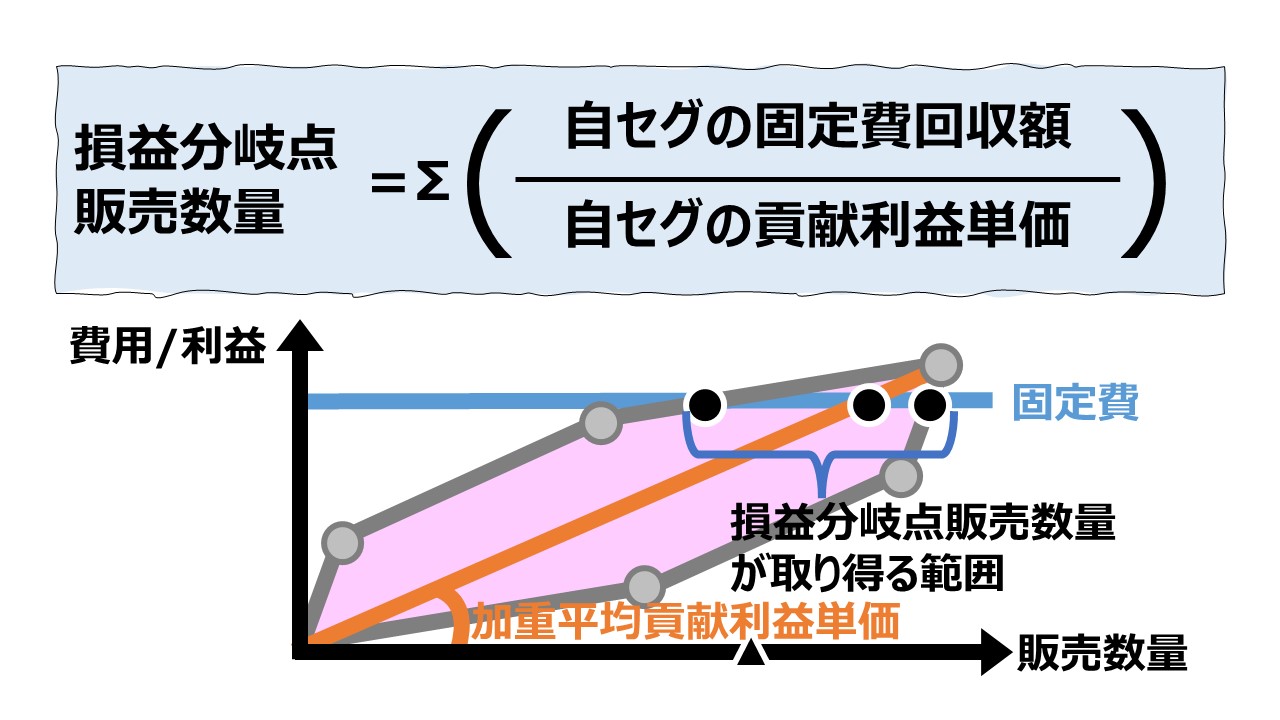
複数セグメントが取り得る貢献利益線の上限と下限の領域の中に加重平均単価線が描画されている。

上限は、最大貢献利益単価のセグメントから販売された場合の最速で損益分岐点販売数量に達する線として描画されている。

下限は、最小貢献利益単価のセグメントから販売された場合の最遅で損益分岐点販売数量に達する線として描画されている。

３本の積み上げ貢献利益線と固定費線の交点のｘ座標がそれぞれの「損益分岐点販売数量」を示している。

損益分岐点販売数量とは別に、各セグメントの販売可能数量を全て合計した「実現販売数量」も描画されている。

閾値としてグラフ表示の限界は以下の通り。

❶固定費はゼロ以下にならなければグラフは崩れない
❷実現販売数量が損益分岐点販売数量に未達の場合でもグラフは崩れない
❸どのセグメント貢献利益線と交わっても損益分岐点販売数量は表示される
❹貢献利益単価がゼロまたはマイナスとなってもグラフは崩れない

【参考】使用しているExcel関数
・INDEX関数、IF関数、LARGE関数、MATCH関数、SMALL関数、SUM関数、SUMPRODUCT関数

解説

個別法（組み合わせ）とそれ以外の計算手法との関係

個別法（組み合わせ）というネーミングに相応しくなく、この計算手法は、幅のある答えとして、上限下限の取りうべきバンドとして損益分岐点販売数量を解として示す。

実は、加重平均貢献利益単価法と個別法（順列）は、それぞれ個別法（組み合わせ）が取り得る解の中に含まれる特殊解の位置付けになっている。

個別法（組み合わせ） が取り得る範囲から、

❶セールスミックスが常に一定である場合は、加重平均貢献利益単価法の解と一致する

❷ユーザ（分析者）が特定のセグメントのセールスミックス（貢献利益の積み上げ順）を選んだ場合は、個別法（順列）の解と一致する

という関係性がある。

すなわち、個別法（組み合わせ）は、この複数セグメントの組み合わせを所与の前提とした場合、実現される可能性のあるすべてのセールスミックスパターンを網羅した範囲（バンド）で損益分岐点販売数量を解として示す。

セールスミックス一定の条件と加重平均貢献利益単価の関係

一般的に、その会社が取りえるすべての複数セグメントのバリエーションと、その期で実現できる販売可能数量の上限の２つの変数の取り合わせで、その会社の損益分岐点販売数量が定まる。

では、その損益分岐点販売数量を決める複数セグメントの組み合わせにも、特有の加重平均貢献利益単価が存在するか、という問題がある。

結論から言うと、個別法（組み合わせ）が示す領域と固定費線が交わる線上のいずれもケースでも、楚の交点まで原点から引かれる直線の傾きは、常にそのケースの加重平均貢献利益単価を表している。

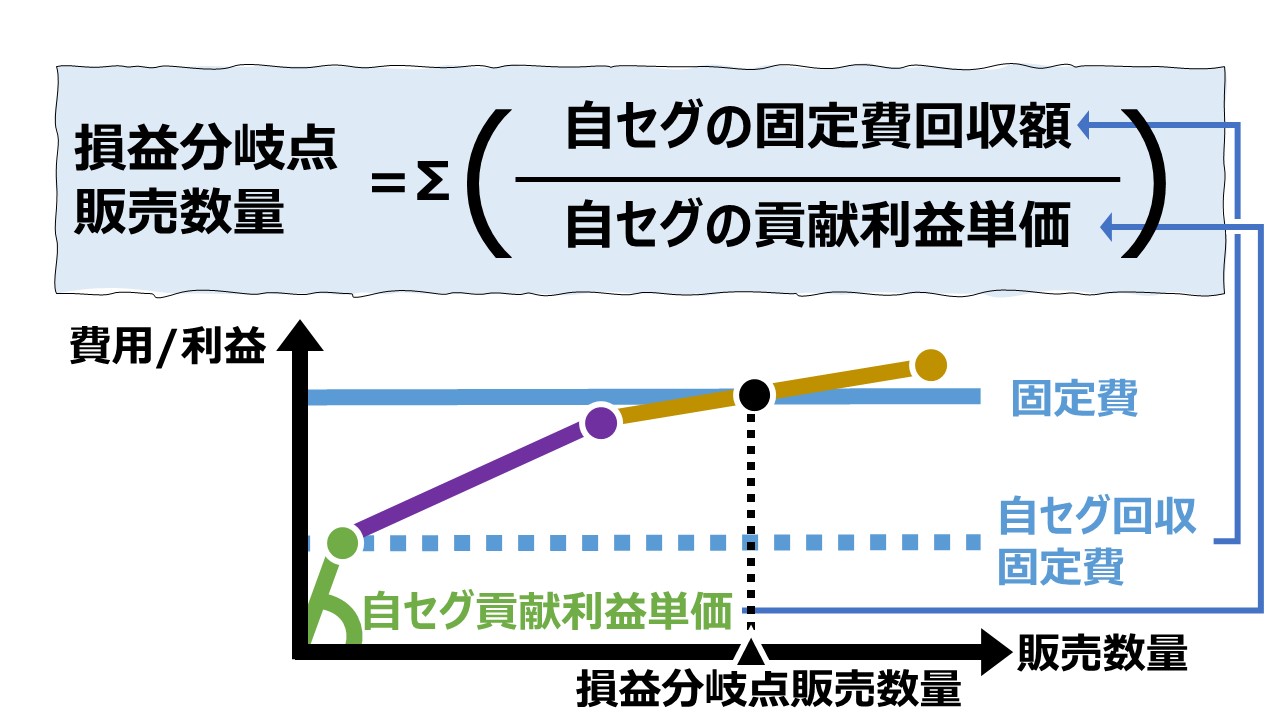
例えば、上限ラインと下限ラインが固定費線と交わる点に対して、原点から直線を引いたものが下図になる。

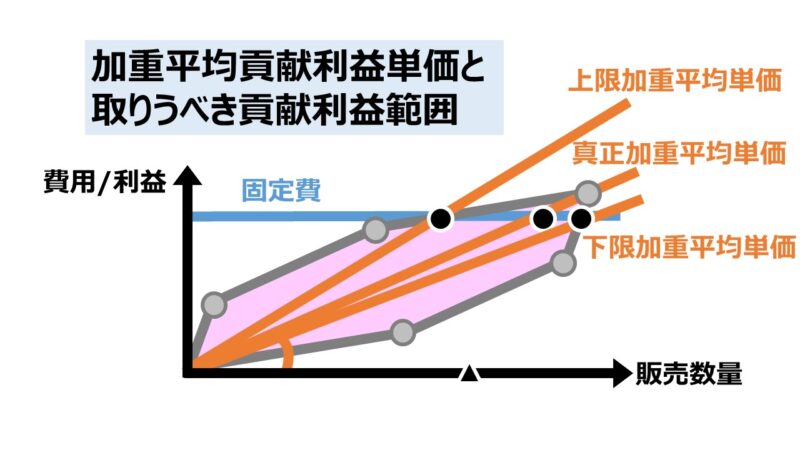
原点から上限ラインと固定費線の交点へ引かれる直線は、「上限加重平均貢献利益単価線」である。

原点から下限ラインと固定費線の交点へ引かれる直線は、「下限加重平均貢献利益単価線」である。

それぞれの交点を実現するまで、常にセールスミックスが一定であるという仮定が成立するなら、貢献利益は販売数量を増やすにしたがって、この直線上を右上へ進むことになる。

「真正加重平均貢献利益単価」は、すべての複数セグメントの販売が完全に終了した後、振り返ってみると、事後的に実現されている加重平均単価となっている。

つまり、実測が完了していないと判明しない。

もちろん、計画フェーズ（予算編成など）で計算される加重平均貢献利益単価も、まだ実現前のあくまで計画/予算上の仮説にすぎない。

どこまで計画シナリオの上振れ下振れを許容範囲とするか、程度問題やその会社の過去実績トレンドからの乖離度からある程度予測がつくのかもしれないが、過度に「加重平均値」に拘った計数管理を行っていると、経営改善の打ち手を講じる最適タイミングと最良の打ち手の選択を見誤るかもしれない。

木を見て森を見ず

ある程度、分かりやすさを犠牲にしても、バンド（幅）をもった目標管理の方が、後々しくじりを少なくしてくれるような気がする（あくまで個人的経験談）。

CVP分析/損益分岐点分析

1	固変分解/貢献利益	変動費、固定費、貢献利益、固変分解
2	損益分岐点分析	様々な損益モデルで損益分岐点を求める
3	CVP分析	金額・単価・数量を変数にした損益モデル
4	CVP分析フレームワークを用いた意思決定	利益最大化を達成するための条件選択方法