- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算手法
単体セグメントで固定費法（貢献利益単価法）により損益分岐点販売数量を求める
販売数量が増減してもセールスミックスが一定（不変）の前提条件が認められる場合、「加重平均貢献利益単価」を用いることで、単体セグメントの場合と同様に、損益分岐点販売数量を求めることができる。
この前提条件を理解するために、まずは単体セグメント（製商品・サービス種類が1種類のみ）における損益分岐点販売数量を求める式を再確認する。
| a/c | 単価 | 数量 | 金額 |
|---|---|---|---|
| 売上高 | @90 | 10 | 900 |
| 変動費 | @30 | 10 | 300 |
| 貢献利益 | @60 | 10 | 600 |
| 固定費 | – | – | 600 |
| 利益 | – | – | 0 |
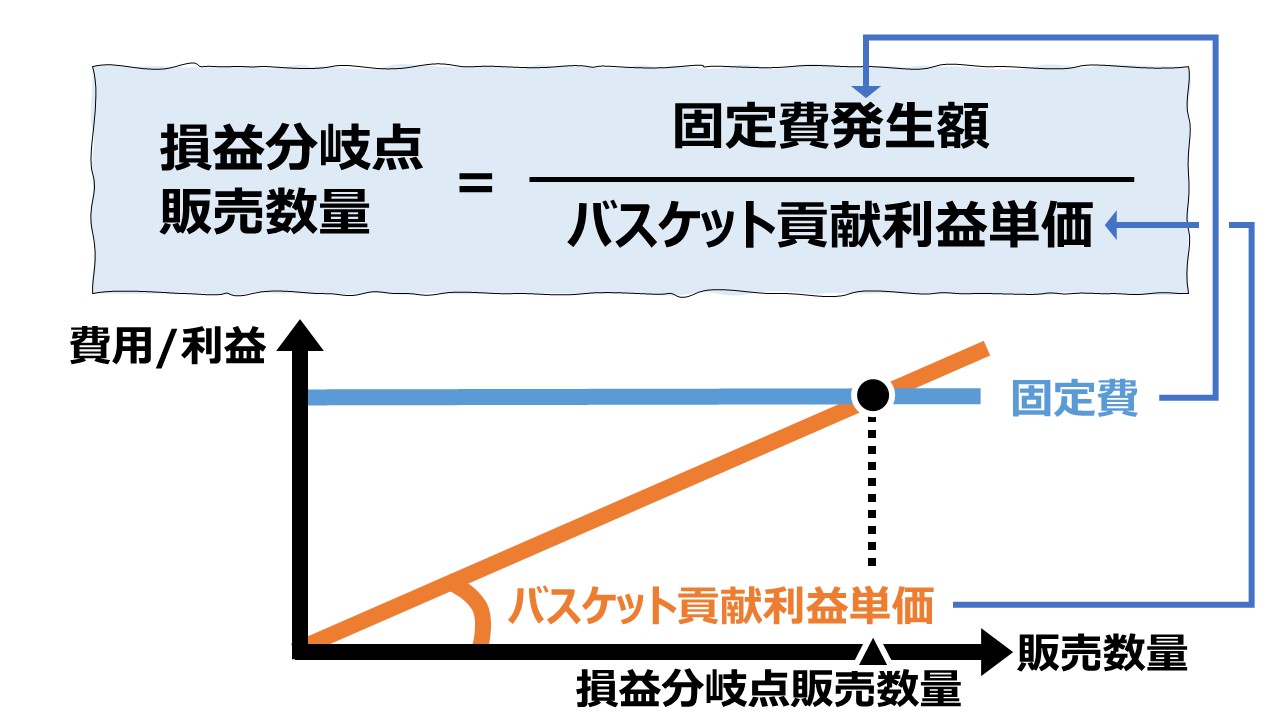
\( \displaystyle \bf 損益分岐点販売数量＝ \frac{固定費}{貢献利益単価}\)
\( \displaystyle \bf 損益分岐点販売数量＝ \frac{600}{@60}\)
\( \displaystyle \bf 損益分岐点販売数量＝ 10\)
セールスミックスが一定（不変）であることと加重平均貢献利益単価の関係
ここに、とある企業がA製品とB製品の2種類の商材を取り扱っているとする。企業の販売数量がどれだけ増減しようと、常にA製品とB製品の売上構成（販売数量構成比）は、40%：60%が維持されるものとする。
企業の販売数量の合計が50個の場合は、A製品は20個販売され、B製品は30個販売される。企業が100個販売する場合は、A製品は40個、B製品は60個販売される。
A製品とB製品それぞれの販売単価（売単価）と変動費単価が下記の通りだったとすると、
| a/c | A製品 | B製品 |
|---|---|---|
| 販売単価 | @400 | @300 |
| 変動費単価 | @250 | @175 |
| 貢献利益単価 | @150 | @125 |
A製品とB製品の加重平均貢献利益単価は、
総販売数量が50個のとき、
| a/c | A製品 | 40% | 金額 | B製品 | 60% | 金額 |
|---|---|---|---|---|---|---|
| 販売単価 | @400 | 20個 | 8,000 | @300 | 30個 | 9,000 |
| 変動費単価 | @250 | 20個 | 5,000 | @175 | 30個 | 5,250 |
| 貢献利益単価 | @150 | 20個 | 3,000 | @125 | 30個 | 3,750 |
加重平均貢献利益単価 = (3,000 + 3,750) ÷ (20個 + 30個)
= 6,750 ÷ 50個
＝@135
総販売数量が100個のとき、
| a/c | A製品 | 40% | 金額 | B製品 | 60% | 金額 |
|---|---|---|---|---|---|---|
| 販売単価 | @400 | 40個 | 16,000 | @300 | 60個 | 18,000 |
| 変動費単価 | @250 | 40個 | 10,000 | @175 | 60個 | 10,500 |
| 貢献利益単価 | @150 | 40個 | 6,000 | @125 | 60個 | 7,500 |
加重平均貢献利益単価 = (6,000 + 7,500) ÷ (40個 + 60個)
= 13,500 ÷ 100個
＝@135
となり、セールスミックスが一定（不変）であるという条件は、常に同じ加重平均貢献利益単価を導くことになる。
そして、それは、総販売数量の増減に関係なく一定値をとるため、それぞれの製品の貢献利益単価に販売数量構成比をそのまま当てて計算しても同じ結果が得られる。
加重平均貢献利益単価 = @150 × 40% + @125 × 60%
= @60 + @75
＝@135
加重平均貢献利益単価から総合計の損益分岐点販売数量を求める
加重平均貢献利益単価は、A製品とB製品の販売構成比から求められた平均単価なので、この平均単価を用いれば、あたかもA製品とB製品をひとつの製品であるかのように計算上扱える。
この加重平均貢献利益単価を既知の単体セグメントの場合における「固定費法（貢献利益単価法）」と同様に、A製品とB製品をあたかもひとつの製品としてみなした場合の損益分岐点販売数量を求めることができる。
| a/c | A製品 | B製品 | 合計/平均 |
|---|---|---|---|
| 販売構成 | 40% | 60% | 100% |
| 販売単価 | @400 | @300 | @340 |
| 変動費単価 | @250 | @175 | @205 |
| 貢献利益 | @150 | @125 | @135 |
| 固定費 | – | – | 74,250 |
| 利益 | – | – | 0 |
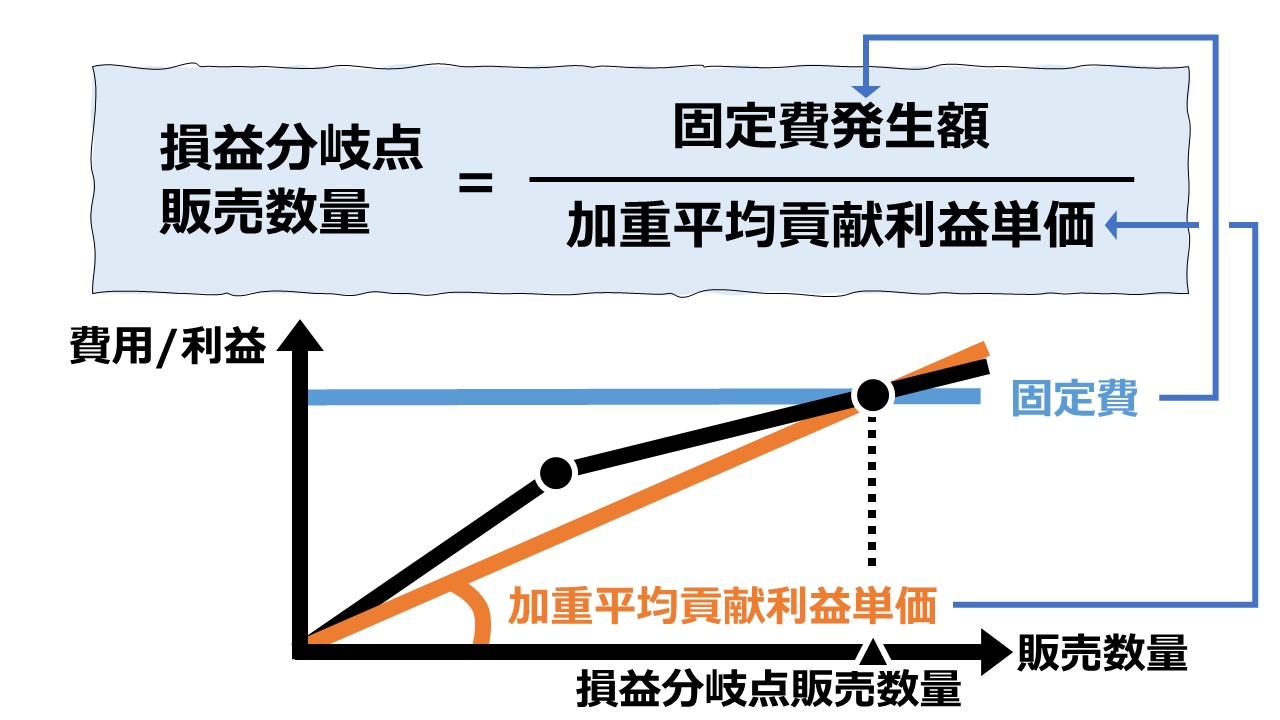
\( \displaystyle \bf 損益分岐点販売数量＝ \frac{固定費}{加重平均貢献利益単価}\)
\( \displaystyle \bf 損益分岐点販売数量＝ \frac{74,250}{@135}\)
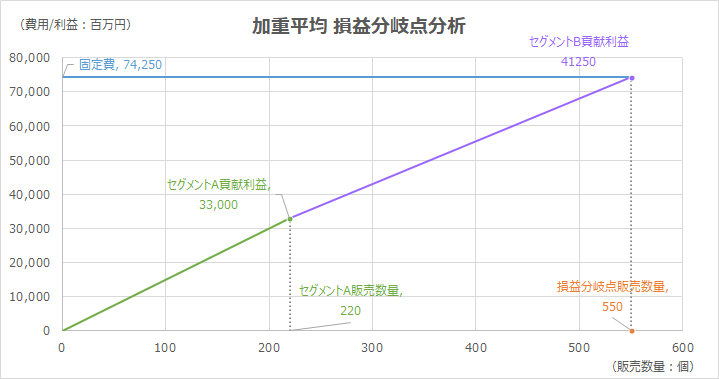
損益分岐点販売数量＝ 550個
各セグメントの損益分岐点販売数量を求める
最終ステップは、加重平均貢献利益単価から算出された総合計の損益分岐点販売数量をベースに、販売構成比率を加味して、各セグメントそれぞれにおける損益分岐点販売数量を求める。
A製品の損益分岐点販売数量 = 550個 × 40% = 220個
B製品の損益分岐点販売数量 = 550個 × 60% = 330個
検算
求められたA製品・B製品の損益分岐点販売数量から逆残で企業全体の損益分岐点販売数量と一致するかを検証する。
| a/c | A製品 | B製品 | 合計/平均 |
|---|---|---|---|
| 販売構成 | 220個 | 330個 | 550個 |
| 販売単価 | @400 | @300 | @340 |
| 売上高 | 88,000 | 99,000 | 187,000 |
| 変動費単価 | @250 | @175 | @205 |
| 変動費 | 55,000 | 57,750 | 112,750 |
| 貢献利益単価 | @150 | @125 | @135 |
| 貢献利益 | 33,000 | 41,250 | 74,250 |
| 固定費 | – | – | 74,250 |
| 利益 | – | – | 0 |
計算プロセス
前章における加重平均貢献利益単価を用いた損益分岐点販売数量の計算式から、以下のシミュレーションプロセスが考えられる。
- 現状分析各セグメントの貢献利益と販売構成を明らかにする
・各セグメントごとの貢献利益単価迄を求める
・販売構成比率の情報を得る - 加重平均貢献利益単価の計算加重平均貢献利益単価を計算する
・各セグメントの貢献利益単価に販売構成比を乗じたものを合計する
- 損益分岐点販売数量の計算複数セグメント トータルの損益分岐点販売数量を求める
・全社固定費を加重平均貢献利益単価で割り算する
- セグメント別損益分岐点販売数量の計算販売構成比から各セグメントごとの損益分岐点販売数量を求める
・会社トータルの損益分岐点販売数量に各セグメントごとの構成比率を乗じる
シミュレーション
Excelテンプレート形式で複数セグメントにおいて、加重平均貢献利益単価法で損益分岐点販売数量を求める計算方法を示す。
入力欄の青字になっている「セグメントA名称（任意の名前）」 「セグメントB名称（任意の名前）」 「販売構成比」「販売単価」「変動費単価」「固定費」に任意の数字を入力すると、加重平均貢献利益単価で損益分岐点販売数量が求められる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
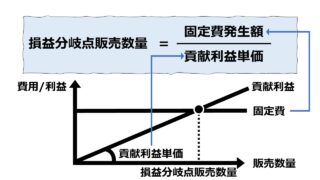
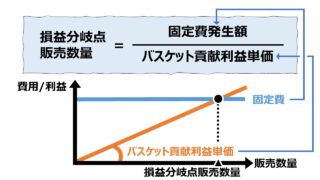
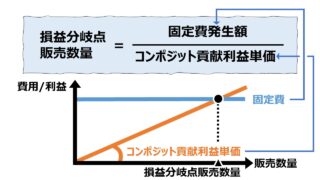
グラフの見方
縦軸が金額である「貢献利益」「固定費」、横軸が販売数量（個）を表している。
水平線が固定費線であり、貢献利益線がセグメントごとに傾き（貢献利益単価）を変えて描画されている。
セグメントAとセグメントBは、より高い貢献利益単価を持つものが原点に近い左方に必ず来るようになっている。それゆえ、貢献利益線は必ず上に凸にならなければならない。
これは、より高い貢献利益単価を持つセグメントのビジネスの方を優先してこなすことで、固定費の早期回収を図るという財務管理の鉄則を表している。
貢献利益線と固定費線の交点が損益分岐点販売数量となる。両者が交わるということは、発生固定費の額と、回収された貢献利益額が同額になることを意味している。
【参考】使用しているExcel関数
・IF関数、CONCAT関数、ROUND関数
解説
単純平均と加重平均の違い
A製品とB製品の平均貢献利益単価を求める際に、
| a/c | A製品 | B製品 |
|---|---|---|
| 販売単価 | @400 | @300 |
| 変動費単価 | @250 | @175 |
| 貢献利益単価 | @150 | @125 |
という情報から、
平均貢献利益単価 = (@150 + @125) ÷ 2 = @137.5
という算術平均（単純平均）を求めてしまうと、今回のセールスミックス問題を解くことはできない。
A製品とB製品の販売構成比が40%：60%にあるとき、B製品の低い単価の影響度の方が多いことをきちんと計算に反映しないと、正確ではないからである。
最終的に、セールスミックスの問題は、それぞれの構成要素（ここではA製品とB製品）の販売数量まで算出する必要があるため、構成数を考慮した加重平均を使用する必要がある。
ちなみに、算術平均（単純平均）は、A製品とB製品の平均単価への影響度がちょうど半分ずつとなるため、構成比率が50%：50%のときのみに正しい特別解となるのである。
セールスミックスが一定であるとの仮定について
実際にビジネスの現場でおきている状況は、セールスミックス自体が、需給バランスやサプライチェーン状のオペレーションの良不良等の様々な要因により常に変動している。
こうした各種制約条件を同時に考慮して損益分岐点販売数量を求めようとするならば、多変量解析などの手法で回帰的（帰納的）に解を求めるか、線形計画法などの手法を用いてシミュレーション値をもとめることになる。
上記のような数学的により高度な手法を用いることが困難な場合は、平均法による買いを求めることをやめ、個別法の採用を検討する必要がある。
ただし、現実はいつも複雑で、人間の脳や理論が追い付いて、常に適切な方法を適用できるとは限らない。
不完全なことを承知しつつ、できるだけシンプルに問題を考えて、解決施策の解決能力のほうを向上させることに努力を傾けた方が事態を好転させるのに役立つかもしれない。
いずれにせよ、そうしたより複雑な計算手法について、本サイトでは別稿で解説する予定である。
管理会計においては、特に金額的影響度の大きい法人税について、観便法として実効税率を用いたグロスアップ計算を適用して、税引後利益から逆残で目標とすべき税前利益やその目標税前利益を達成するための売上高などの諸条件を決めていく際に用いられることが多い。
CVP分析/損益分岐点分析
| 1 | 固変分解/貢献利益 | 変動費、固定費、貢献利益、固変分解 |
| 2 | 損益分岐点分析 | 様々な損益モデルで損益分岐点を求める |
| 3 | CVP分析 | 金額・単価・数量を変数にした損益モデル |
| 4 | CVP分析フレームワークを用いた意思決定 | 利益最大化を達成するための条件選択方法 |
コメント