- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
CVP分析と損益分岐点分析の関係とは
意外にこの2つの関係性について正鵠を得た解説を目にすることは少ない。
CVPは、Cost, Volume, Profit の略で、営業量（Volume）の変化がコストおよび利益にどういう影響を及ぼすかを明らかにするものである。
そして、利益がゼロ、すなわち、固定費と貢献利益の値が一致する営業量を損益分岐点と呼ぶ。
つまり、CVP分析において、損益分岐点を達成する営業量（Volume）を求めるが損益分岐点分析ということになる。
\( \displaystyle \bf 損益分岐点分析 \subset CVP分析 \)
広義のCVP分析に狭義の損益分岐点分析が含まれる関係にある。
損益分岐点であることの意味とは
「損益分岐点」とは損益トントンである営業量（Volume）になっていることを意味する。
損益トントンというのは、売上高と総コストが同額（一致）して、利益ゼロとなることを指す。
営業量（Volume）は、企業による収益活動のための活動量のことを指す。ここでは理解を促すために、「売上高」とか「稼働率」で測定できるものと軽くイメージしておくとよい。
つまり、「損益分岐点」とは、売上高と総コストが一致するような「売上高」そのもの、またはその売上高をちょうど稼ぎ出せる企業の生産能力（サービス提供能力）の「稼働率」を指す。
損益トントンであることの意味とは
「損益トントン」とは、最終的な利益がゼロの状態のことを指す。
売上高 – 総コスト = 0
売上高 – (変動費 + 固定費) = 0
(売上高 – 変動費) = 固定費
貢献利益 = 固定費
上式のように、「損益トントン」の損益（利益）は最終利益のことを指し、最終利益は貢献利益から固定費を差し引いたものになる。
よって、「損益トントン」は、貢献利益と固定費の額が一致（同額）であることを意味する。
損益トントンの式から損益分岐点を求めるには
もう一度、損益トントンの式を再掲する。
貢献利益 = 固定費
この式は、損益トントンという結果を示すだけで、このままでは損益トントンとなる営業量を知ることはできない。
損益トントンとなる営業量を知るためには、左辺の貢献利益の項に営業量を要素を加えて変形させてやればよい。
営業量（Volume）として「売上高」を求める
貢献利益を売上高の数字を使って表すと、
貢献利益 = 貢献利益率(%) × 売上高
これを、損益トントンの式に代入すると、
貢献利益 = 固定費
貢献利益率(%) × 売上高 = 固定費
これを売上高で解くと、
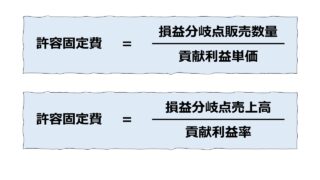
\( \displaystyle \bf 売上高_{BEP} = \frac{固定費}{貢献利益率(\%)} \)
こうして、損益分岐点売上高（売上高BEP）を求める式を得ることができた。
仮に、売上高：1000、固定費：400、貢献利益率：40% とすると、
\( \displaystyle \bf 1000 = \frac{400}{0.4} \)
となって、式が成立していることがわかる。
営業量（Volume）として「販売数量」を求める
貢献利益を販売数量の数字を使って表すと、
貢献利益 = @貢献利益単価 × 販売数量
これを、損益トントンの式に代入すると、
貢献利益 = 固定費
@貢献利益単価 × 販売数量 = 固定費
これを販売数量で解くと、
\( \displaystyle \bf 販売数量_{BEP} = \frac{~~~~~~~~~~固定費~~~~~~~~~~~~~~~}{@貢献利益単価~~~~~} \)
こうして、損益分岐点販売数量（販売数量BEP）を求める式を得ることができた。
仮に、販売数量：50、固定費：400、@貢献利益単価：8 とすると、
\( \displaystyle \bf 50 = \frac{400}{8} \)
となって、式が成立していることがわかる。
損益分岐点売上高と損益分岐点販売数量の関係とは
前章で、いきなり仮定とはいえ、貢献利益率：40%や、貢献利益単価：@8 が都合よく登場して、あまりにきれいに等式を成立させるために無理やり当てはめているのではと勘繰りたくなるかもしれない。
それでは、すべての関係が関連付けられている損益分岐点の世界観についてできるだけわかりやすい解説を試みる。
もう一度、基本に立ち返って、利益恒等式からひも解くことにする。
売上高 – (変動費 + 固定費) = 利益
変動費を貢献利益率(%)で表すために、以下のように式を変形してみる。
売上高 – 変動費 = 固定費 + 利益
(1 – 変動費比率) × 売上高 = 固定費 + 利益
貢献利益率(%) × 売上高 = 固定費 + 利益
この時、売上高：1000、貢献利益率：40%、固定費：400 で損益トントンだとすると、
40% × 1000 = 400 + 0
400 = 400
無事、利益恒等式が成立し、この時に与えられた条件が損益分岐点のものであることが証明できた。
同じことを、今度は販売数量に置き換えてやってみる。
売上高 – (変動費 + 固定費) = 利益
売上高は 販売単価×販売数量 で表され、貢献利益単価 = 販売単価 – 変動費単価 で表されるので、
売上高 – 変動費 = 固定費 + 利益
(販売単価 × 販売数量) – (変動費単価 × 販売数量) = 固定費 + 利益
(販売単価 – 変動費単価) × 販売数量 = 固定費 + 利益
貢献利益単価 × 販売数量 = 固定費 + 利益
この時、販売数量：50、貢献利益単価：@8、固定費：400 で損益トントンだとすると、
@8 × 50 = 400 + 0
400 = 400
今度も無事、利益恒等式が成立し、この時に与えられた条件が損益分岐点のものであることが証明できた。
だとすれば、変動費と固定費という総コスト関数の内容が変わらずに、売上高と販売数量という営業量（Volume）の表現方式の違いだけが差ということは、同じコスト条件ならば、その売上高と販売数量の間には一定の関係があることがわかる。
売上高 = 販売単価 × 販売数量 ･･･ 式１
売上高：1000、販売単価：@20、販売数量：50 ならば、
1000 = @20 × 50
1000 = 1000
ということになる。
式１から、損益分岐点分析において、ただひとつのコスト関数が設定されている場合、損益分岐点売上高と損益分岐点販売数量は、常に式1を成立させるような一定の関係にあることがわかる。
損益分岐点売上高と損益分岐点販売数量の読み替えとは
前章にあるように、コスト関数がひとつ設定された場合の損益分岐点売上高と損益分岐点販売数量は、
売上高 = 販売単価 × 販売数量 ･･･ 式１
を常に成り立たせるように一意に決まる。
さらに、「損益分岐点売上高」を決定するためのキーとなるのが「貢献利益率（%）」であり、「損益分岐点販売数量」を決定するためのキーとなるのが「@貢献利益単価」である。
これらの性質を利用することで、「貢献利益率（%）」がわかれば「@貢献利益単価」を求めることができ、反対に、「@貢献利益単価」がわかれば「貢献利益率（%）」を求めることができる。
この双方向の読み替えを簡単な式の形で頭に入れておけば、経営計画・予算編成や商品企画といった場面で、損益分岐点分析がやりやすくなると思われる。
@貢献利益単価を貢献利益率（%）から求める
貢献利益単価は、製商品・サービスの一単位当たりの貢献利益率でもある。
ひとつ20円の貢献利益単価の商品の販売単価が80円ならば、その商品の貢献利益率は25%である。
@20円 = 25% × @80円
この 25% という売上高貢献利益率は、ひとつひとつの商取引での販売価格が一定ならば、商品ひとつで計算しても、同じ商品の売上高を合計してから計算しても同じ25%になる。
ここから、下式が導かれる。
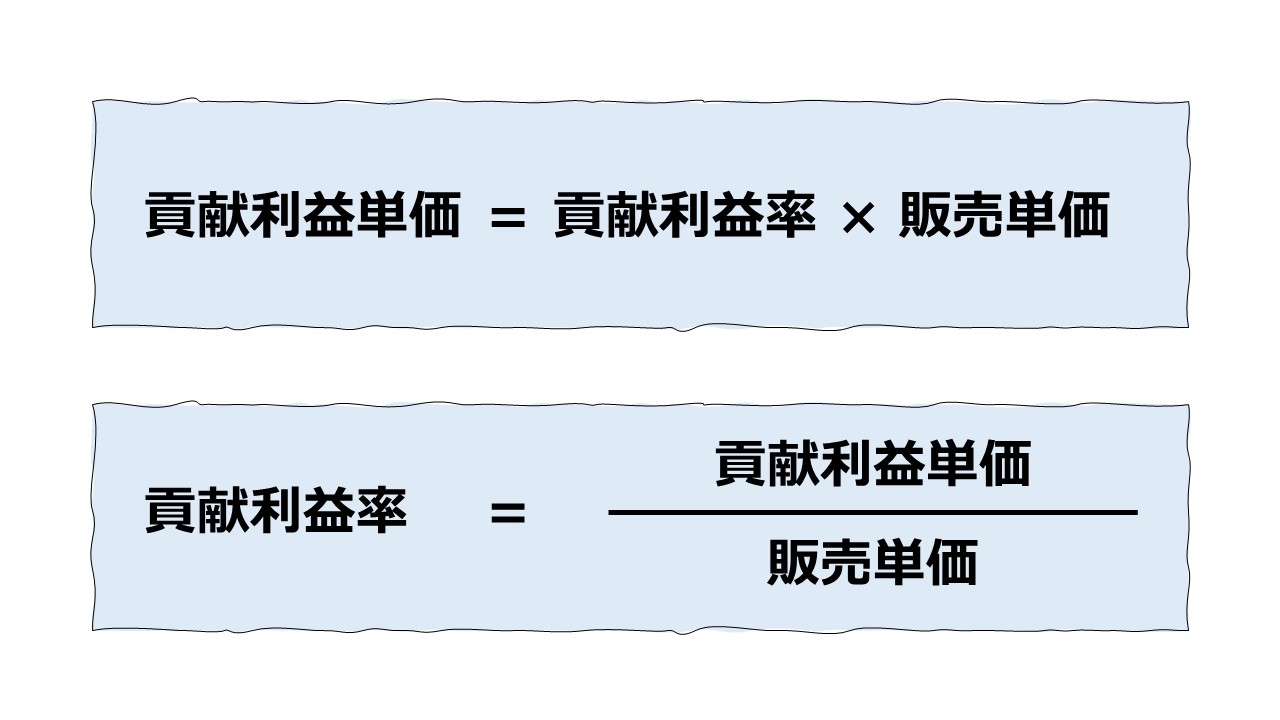
@貢献利益単価 = 貢献利益率（%）× @販売単価
貢献利益率（%）を@貢献利益単価から求める
貢献利益率は、製商品・サービスの売上高に対する貢献利益の割合を示す。
売上高が800円で貢献利益が200円の場合は、下式のようになる。
25% = 200円 ÷ 800円
貢献利益の割合を計算するのに、ひとつひとつの商取引での販売価格が一定ならば、商品ひとつで計算しても、同じ商品の売上高を合計してから計算しても同じになる。
25% = @20円 ÷ @80円
ここから、貢献利益率は、販売単価と貢献利益単価に関する情報が手元にあれば、計算することができる。
貢献利益率（%）= @貢献利益単価 ÷ @販売単価
これにより、事業計画や商品企画の場面で、貢献利益率から貢献利益単価を求めて、損益分岐点販売数量を導くことができるようになるし、反対に、貢献利益単価から貢献利益率を求めて、損益分岐点売上高を求めることができるようになる。
シミュレーション
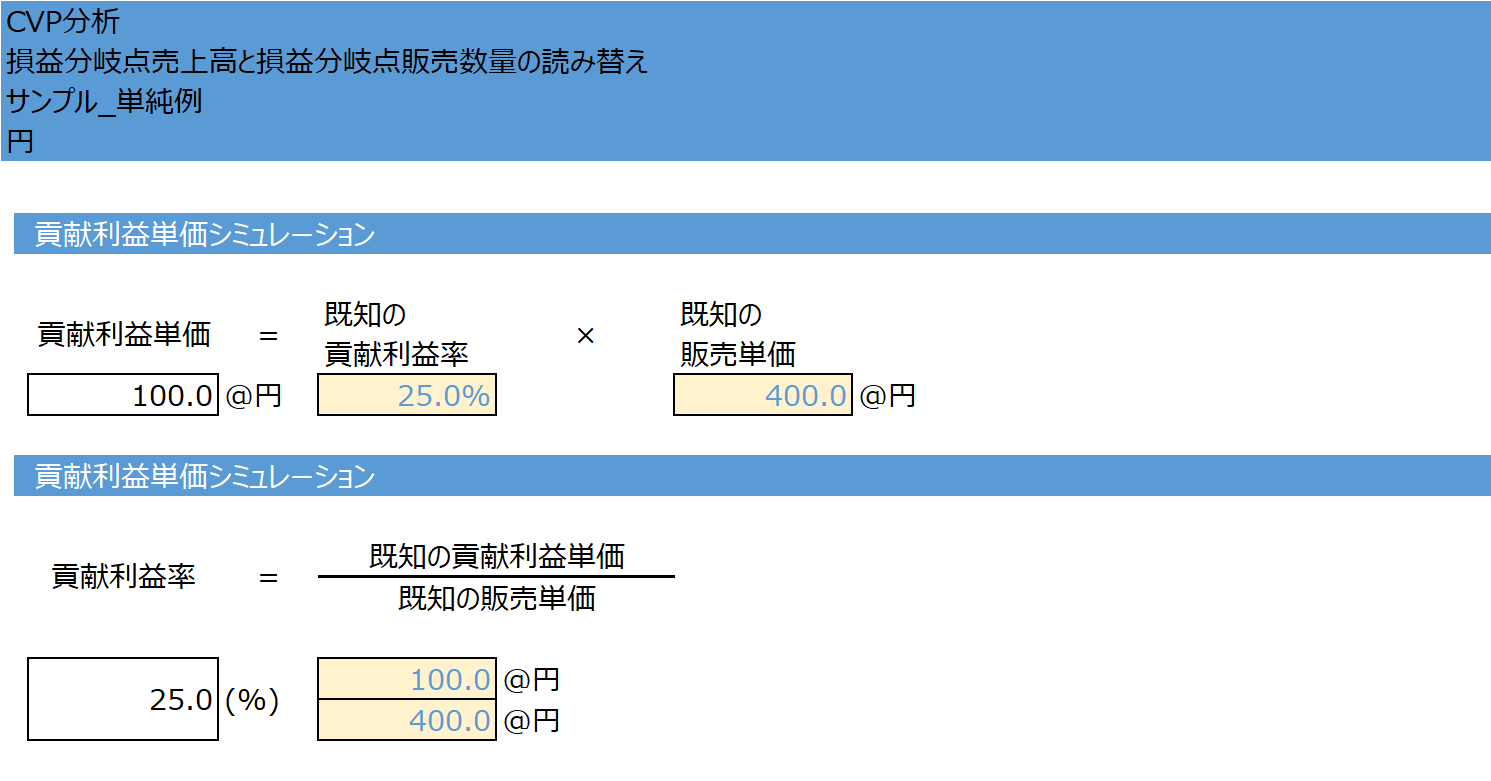
Excelテンプレート形式で損益分岐点売上高と損益分岐点販売数量の読み替えの計算方法を示す。
入力欄の青字になっている「既知の貢献利益率」「既知の販売単価」「既知の貢献利益単価」に任意の数字を入力すると、それぞれ、目標とする貢献利益単価、貢献利益率が求められる。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
CVP分析/損益分岐点分析
| 1 | 固変分解/貢献利益 | 変動費、固定費、貢献利益、固変分解 |
| 2 | 損益分岐点分析 | 様々な損益モデルで損益分岐点を求める |
| 3 | CVP分析 | 金額・単価・数量を変数にした損益モデル |
| 4 | CVP分析フレームワークを用いた意思決定 | 利益最大化を達成するための条件選択方法 |
粗利、変動費、固定費の関係で儲ける会社づくりをストーリー仕立てで理解できる。
管理会計入門書。CVP分析や固変分解の基礎がわかる。
コメント