(再考)損益分岐点の意味
CVP分析とは、英語の Cost-Volume-Profit Analysis の省略形であり、Volume(営業量)の増減が Cost(コスト)をどのように変化させて、Profit(利益)を生み出すのかを線形回帰のフレームワークで明らかにするものである。
簡単に言い換えると、与えられたコストの発生条件下で、販売数量や売上金額を自由に変化させてみて、利益がトントンになる販売数量や売上金額を一意に導き出す計算技法である。
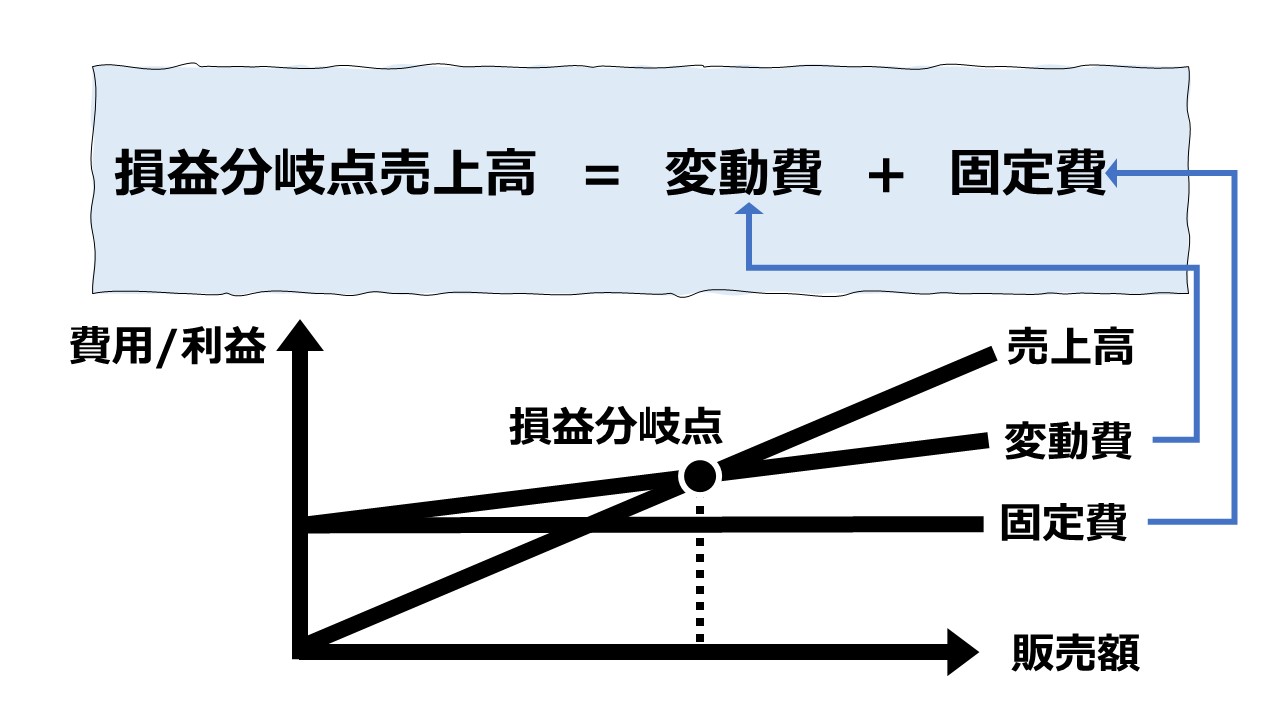
販売数量や売上高の変化に伴い、常に一定額であると仮定されるのが固定費である。
販売数量や売上高の変化に伴い、常に一定比率を保ちつつ、販売数量や売上高の増減に比例して同じ方向に増減すると仮定するのが変動費である。
利益が赤字でもなく黒字でないトントンである状態は、損益分岐点(Breakeven Point)であると呼ばれる。
CVP分析の結果、様々な値をとりえる販売数量や売上高が損益がトントンとなる特異点を探すことの重要性は、
①損益分岐点が最低ラインとなるような具体的な販売目標の設定に役立つ
②変動費単価や固定費発生額に対するコストダウンの目標水準の設定に役立つ
からである。
公式として損益分岐点の計算式の背景にあるもの
損益分岐点を求める計算ロジックを公式として人間の脳に記憶しやすい形に加工して公式化すると、あとは機械的に、与えられた変数を公式に放り込むだけで、損益分岐点情報が得られる。
各種資格試験においても、公式を丸暗記して、できるだけ効率的に試験での得点力を上げようとする向きも多いことだろう。
Volume(営業量)に対して、販売数量と売上高という数量情報を基礎にするか、金額情報を基礎にするかで、損益分岐点を求める公式の構成は大きく2つに大別される。
しかし、その背景には、損益分岐点では、売上高とコスト総額が同額になる(一致する)という恒等式が存在し、各種公式はこれを計算問題で条件で与えられる変数を放り込みやすいように変形しているに過ぎない。
迂遠なようでも、筆者は、会計系の資格試験において、損益分岐点にまつわる各種公式をすべて記憶せずに、たった一つの恒等式のみを記憶したうえて、題意に対して、必要に応じて変形して使いまわしていたにすぎない。
@s × Q = @v × Q + FC + P
@s:販売単価
Q:販売数量
@v:変動費単価
FC:固定費発生額
P:利益額
記号で表された上式を日本語に置き換えると、
販売単価 × 販売数量 = 変動費単価 × 販売数量 + 固定費発生額 + 利益
損益分岐点とは、利益がゼロなので、上式の利益(P)にゼロを代入すると、
販売単価 × 販売数量 = 変動費単価 × 販売数量 + 固定費発生額 + 0
両辺に販売数量が登場しているのはダブっている証拠だから移項によりこれを整理できる、
と同時に、日本語で固定費発生額の表記を簡略化のためにただの「固定費」と書き改めると、
(販売単価 – 変動費単価) × 販売数量 = 固定費
左辺から損益分岐点販売数量だけを取り出すと、
\( \displaystyle \bf 損益分岐点販売数量 = \frac{~~~~~~~~~固定費~~~~~~~~~~~~~~~~~}{(販売単価 – 変動費単価)~~~~~~~~} \)
これで、
①販売単価
②変動費単価
③固定費発生額
の3つが与えられれば、損益分岐点販売数量を算出できる公式を導出することができた。
損益分岐点販売数量を求める
損益分岐点販売数量を求める公式は、前章で示した通り、販売単価、変動費単価、固定費の3要素から成る。
\( \displaystyle \bf 損益分岐点販売数量 = \frac{~~~~~~~~~固定費~~~~~~~~~~~~~~~~~}{(販売単価 – 変動費単価)~~~~~~~~} \)
題意によっては、余計な親切心で、販売単価と変動費単価に代えて、貢献利益単価が示されている場合もある。
販売単価 – 変動費単価 = 貢献利益単価
という関係が成り立っているので、公式中の分母にある「販売単価 – 変動費単価」を「貢献利益単価」に置き換えるだけでよい。
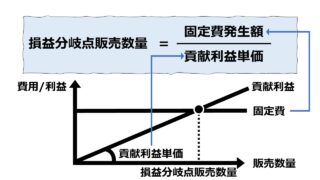
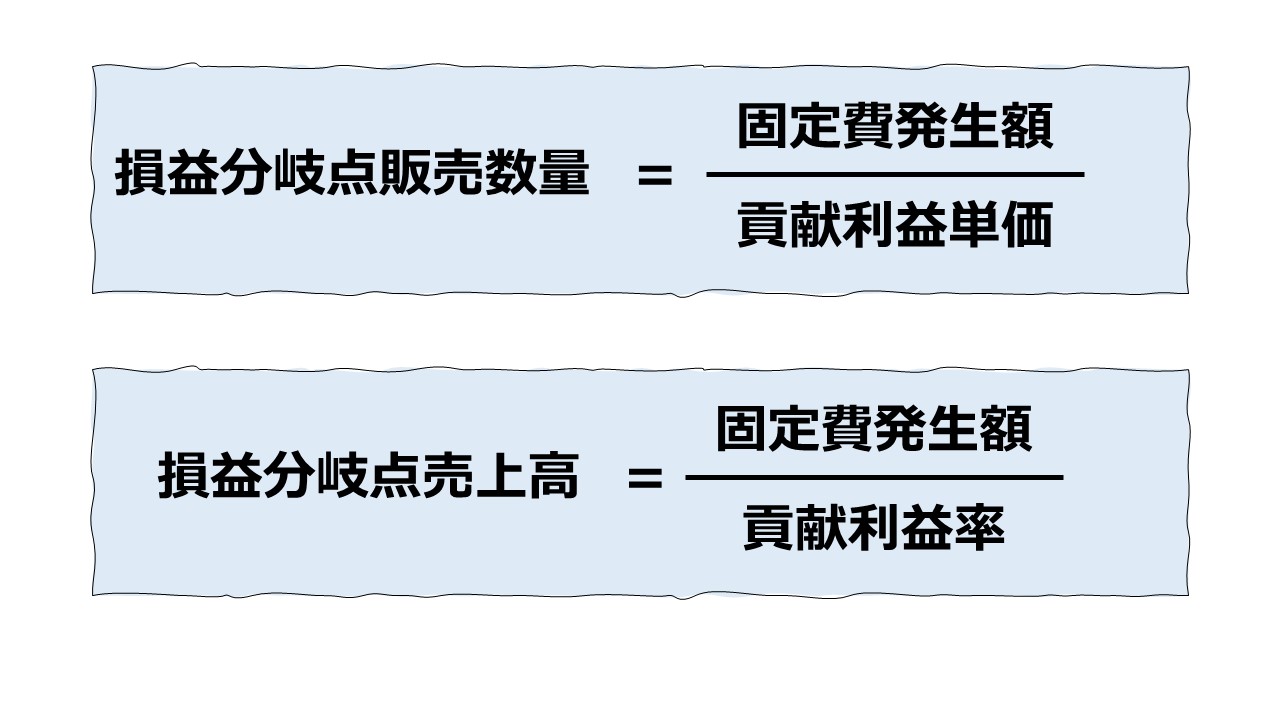
\( \displaystyle \bf 損益分岐点販売数量 = \frac{固定費}{貢献利益単価} \)
そもそも、貢献利益とは、固定費の回収に役立ち、回収分をうわまったら企業に利益をもたらすのに貢献してくれることを示して「貢献」とネーミングされている。
よって固定費と貢献利益の関係は至極相性が良くて当然なのである。
損益分岐点売上高を求める
CVP分析、損益分岐点分析において、分析対象となる営業量が、数量で示されるものもあれば、金額で示されるものもある。
複数種類の製商品・サービスをひとまとめにして損益分岐点を求めたいときや、そもそも営業量そのものを計量することができずに、結果としての販売金額でしか示せないケースに有効活用できる手法である。
この場合でも、損益分岐点売上高を求める公式は、前章で示した損益分岐点販売数量の公式の該当箇所を数量情報から金額情報に置き換えるだけである。
損益分岐販売数量を求める公式を再掲する。
\( \displaystyle \bf 損益分岐点販売数量 = \frac{固定費}{貢献利益単価} \)
結論から記述すると、左辺の「損益分岐点販売数量」を「損益分岐点売上高」、「貢献利益単価」を「貢献利益率」に置き換えるだけである。
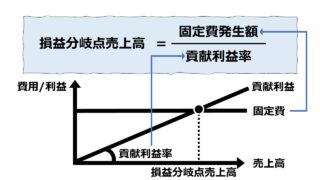
\( \displaystyle \bf 損益分岐点売上高 = \frac{固定費}{貢献利益率} \)
通常、貢献利益率は、下記の2つの方法で求められる。
\( \displaystyle \bf 貢献利益率 = \frac{販売単価 – 変動単価}{販売単価} \)
\( \displaystyle \bf 貢献利益率 = \frac{売上高- 変動費}{売上高} \)
売上高 = 販売単価 × 販売数量、
変動費 = 変動費単価 × 販売数量、
という計算で求められることを我々は知っているので、貢献利益率も詰まる所、販売単価と変動費単価と販売数量から求められることも簡単に理解できるだろう。
したがって、貢献利益情報を使う前の公式の形でこれを表すと次のようになる。
\( \displaystyle \bf 損益分岐点売上高 = \frac{固定費}{\left(\frac{販売単価 – 変動費単価}{販売単価}\right)} \)
題意によっては、余計な親切心で、販売単価と変動費単価に代えて、貢献利益単価が示されている場合もある。
となれば、最初歩の代数の知識と四則演算の技法を知っているだけで、次の恒等式をひとつだけ理解しておけば、管理会計実務において、直線回帰(単回帰)の世界でのみ語られるCVP分析なら十分に適用できる便利なツールとして使いこなせるはずである。
@s × Q = @v × Q + FC + P
@s:販売単価
Q:販売数量
@v:変動費単価
FC:固定費発生額
P:利益額
(おまけ)損益分岐点販売数量と損益分岐点売上高の切り替え
管理会計実務においては、数量情報を有する損益分岐点販売数量の形でCVP分析を行うほうが情報量が多いため、複数種類の製商品・サービスをまとめて取り合うとか、計量単位が金額意外に取れない場合以外に、好んで情報量がより少なくなる損益分岐点売上高ベースのCVP分析を採用するメリットはない。
しかし、会計系の資格試験では往々にして、試験のための問題が出題されることがある。その代表的なものの一つが、損益分岐点販売数量と損益分岐点売上高の読み替えの問題だ。
ここでは、前章までの公式の展開や変換の理解を助けるためにこの読み替えの説明を試みる。
しかし、管理会計実務において真剣にこの読み替え技法がその本領を発揮してきた場面を筆者は寡聞にして知らない。
まず、損益分岐点販売数量と損益分岐点売上高の公式を再掲する。
\( \displaystyle \bf 損益分岐点販売数量 = \frac{~~~~~~~~~固定費~~~~~~~~~~~~~~~~~}{(販売単価 – 変動費単価)~~~~~~~~} \)
\( \displaystyle \bf 損益分岐点売上高 = \frac{固定費}{\left(\frac{販売単価 – 変動費単価}{販売単価}\right)} \)
一見して、2つの公式には、共通して「固定費」が含まれていることがわかる。
よって代入法を用い、損益分岐点販売数量の式を損益分岐点売上高の公式中の固定費に代入することで両式を統合してみよう。
まず、損益分岐点販売数量の公式を「固定費」で解くと、
\( \displaystyle \bf 固定費 = 損益分岐点販売数量 \times (販売単価 – 変動費単価) \)
この右辺を損益分岐点売上高の公式中の「固定費」に代入すると、
\( \displaystyle \bf 損益分岐点売上高 = \frac{損益分岐点販売数量 \times (販売単価 – 変動費単価)}{\left(\frac{販売単価 – 変動費単価}{販売単価}\right)} \)
右辺の分子分母から (販売単価 – 変動費単価) を除くと、
\( \displaystyle \bf 損益分岐点売上高 = \frac{損益分岐点販売数量}{\left(\frac{1}{販売単価}\right)} \)
右辺の分子分母に販売単価をかけると、
\( \displaystyle \bf 損益分岐点売上高 = 販売単価 \times 損益分岐点販売数量 \)
この読み替えの公式は、上記のような式の展開をわざわざ試みなくても、損益分岐点販売数量に販売単価をかければ、単価×数量=金額 という関係が成立するのは直観でわかるので、この公式は見ただけで理解できる。
しかし、これを損益分岐点販売数量への変換を行う式に変形すると、
\( \displaystyle \bf 損益分岐点販売数量 = \frac{損益分岐点売上高}{販売単価} \)
となり、さすがにこの式は一見するだけでは直観的に式の意味するところを把握するのは難しいかもしれない。
そのために上述のような「固定費」の代入法で2つの公式を統合して見せたわけだ。
損益分岐点にまつわる公式はそれを記憶していて、各種試験などで効率よく問題を解くのに利用できればそれに越したことはない。
しかし、万一、公式を忘れたとしても、また、計算結果を検算する必要が生じたとしても、管理会計実務において何が与件で何を目的変数として解を求めるのか臨機応変に対応すべき状況に陥ったとしても、次の式を一つだけは必ず明記しておくことが有用であることは間違いない。
@s × Q = @v × Q + FC + P
@s:販売単価
Q:販売数量
@v:変動費単価
FC:固定費発生額
P:利益額
 CVP分析/損益分岐点分析
CVP分析/損益分岐点分析
| 1 | 固変分解/貢献利益 | 変動費、固定費、貢献利益、固変分解 |
| 2 | 損益分岐点分析 | 様々な損益モデルで損益分岐点を求める |
| 3 | CVP分析 | 金額・単価・数量を変数にした損益モデル |
| 4 | CVP分析フレームワークを用いた意思決定 | 利益最大化を達成するための条件選択方法 |
粗利、変動費、固定費の関係で儲ける会社づくりをストーリー仕立てで理解できる。
管理会計入門書。CVP分析や固変分解の基礎がわかる。
コメント