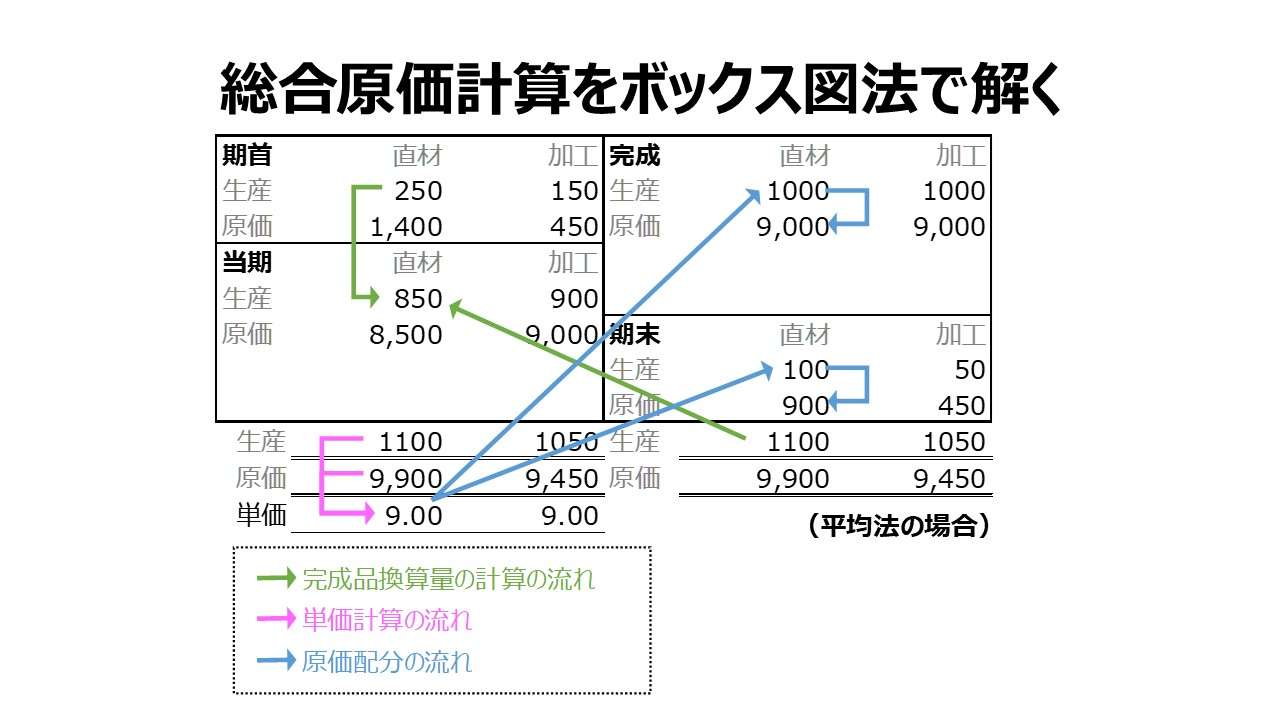
総合原価計算をボックス図法で解く

総合原価計算をボックス図法で解く

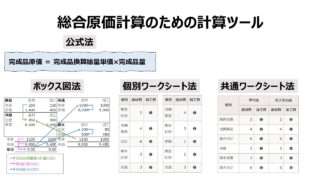
計算ツールの種類

総合原価計算の各種計算ツールとしてよく挙げられるのが、❶公式法、❷ボックス図法、❸ワークシート法 の３つである。このうち、ワークシート法については、平均法と先入先出法のそれぞれに固有のフォーマットを適用する、❸-1:個別ワークシート法、いずれにも共通のフォーマットを適用する、❸-2：共通ワークシート法 に分けることもある。

ここでは❷ボックス図法について解説する。

各計算ツールの大まかな説明・比較は以下の通り。

計算ツール	計算方針	平均法	[第1法]修正FIFO-簡便法	[第2法]修正FIFO-原価計算基準 準拠法	[第3法]純粋FIFO-米国法	[第4法]純粋FIFO-プロセス準拠法
公式法	単価方式	◎	〇	〇	〇	△
	数量按分方式	◎	〇	〇	〇	△
ボックス図法	単価方式	◎	◎	〇	△	✖
	数量按分方式	✖	✖	✖	✖	✖
個別ワークシート法	単価方式	◎	△	ー	〇	ー
共通ワークシート法	単価方式	〇	〇	ー	◎	ー

ボックス図法の特徴

ボックス図法は、会計系資格試験において、計算問題を素早く手書きで解く場合に最適な解法である。

借方貸方からなる丁勘定をボックス図という表記法により可視化し、ボックス内に換算量や原価額を、ボックス外に単価情報など書き入れていき、期末仕掛品原価と完成品原価に原価配分していく方法である。

総合原価計算の計算ロジックの学習にも使えるが、とにかく計算を手早く処理することに適する。特に、先入先出法の簡便法においてはその長所をいかんなく発揮する。多少複雑になるものの、工程別計算や連産品原価計算、仕損減損処理にも応用できる優れものだ。

一般的には、典型的な計算問題にもあるように、始点投入前提の直接材料費と平均的投入前提の加工費とで完成品換算量の推計値が別々になることが多いことから、ボックス図は、直接材料費と加工費の2種類の科目別に用意されることが多い。

ボックス図の描き方で、いくつかのバリエーションが生じる。

図法	総ボックス数	完成品換算量 ボックス数	原価ボックス数	特徴
1⃣集約図法	1	（1つに集約）	（1つに集約）	全要素を1つのボックスに収納する
2⃣科目集約図法	2	1	1	直材費と加工費の2つのボックスを用いる
3⃣原価集約図法	3	2	1	完成品換算量だけ直材費と加工費のボックスを分ける
4⃣換算量集約図法	3	1	2	原価だけ直材費と加工費のボックスを分ける
5⃣個別図法	4	2	2	完成品換算量も原価も直材費と加工費のボックスを用意する

計算結果は同じになるので、上記図法に関しては原則として個人的な好みの問題かもしれない。仕損減損や工程別計算など、特定領域の出題や、出題意図が原価配分なのか製品単価を求めているのかによってはそれぞれに最適な図法がある。

しかしながら、日商簿記など資格試験で素早い計算目的を達成するには、どれか一つに絞って自分なりの型を作った方が効率的かもしれない。

次章で、「平均法」「材料は始点投入」のケースでこの5つの図法をそれぞれ紹介する。

設例

ボックス図法を習得するにあたり、5つの図法の違いを具体例をもって理解するため、以下の設例を用いる。

なお、「総合原価計算を公式法で解く」にあったように、原価配分には数量按分方式と単価計算方式の２つが存在するが、以下のボックス図法では、いずれも単価計算方式を採用している。

「資料」は次の通り。なお、材料は始点投入されるものとする。

[生産データ]
期首仕掛品　　250kg（進捗度60%）
当期受入量　　850kg
完成品　　　 1000kg
期末仕掛品　　100kg（進捗度50%）

[原価データ]
期首仕掛品原価　1,850円
　直接材料費　　1,400円
　加　工　費　　　450円
当期製造費用 　17,500円
　直接材料費　　8,500円
　加　工　費　　9,000円

前捌きとして、期首仕掛品換算量・期末仕掛品換算量を先に求めておく。

●直接材料費
\( \displaystyle \bf 期首仕掛品換算量 = 期首仕掛品 \times 進捗度 = 250kg \times 100\% = 250kg \)
\( \displaystyle \bf 期末仕掛品換算量 = 期末仕掛品 \times 進捗度 = 100kg \times 100\% = 100kg \)

●加工費
\( \displaystyle \bf 期首仕掛品換算量 = 期首仕掛品 \times 進捗度 = 250kg \times 60\% = 150kg \)
\( \displaystyle \bf 期末仕掛品換算量 = 期末仕掛品 \times 進捗度 = 100kg \times 50\% = 50kg \)

平均法

集約図法

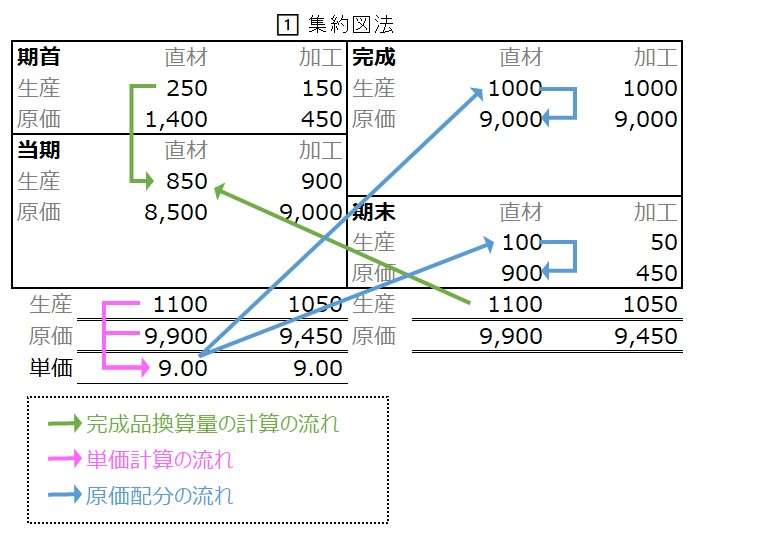
集約図法は、全ての要素をひとつのボックス図に書き入れる図法である。一覧性に優れているが、ボックス内で数字が混雑するので、作図する際に戸惑うかもしれない。

関連する数値が近接しているため、手書き計算の際にお目当ての数値を探すのにあまり苦労しないというメリットがある。

灰色文字は、配置を決め打ちにしていれば、わざわざ書き込む必要はない。資格試験対策として事前練習を積み重ねていけば、やがていちいち書き込まなくても相対的位置で判別できるようになる（はず）。

科目集約図法

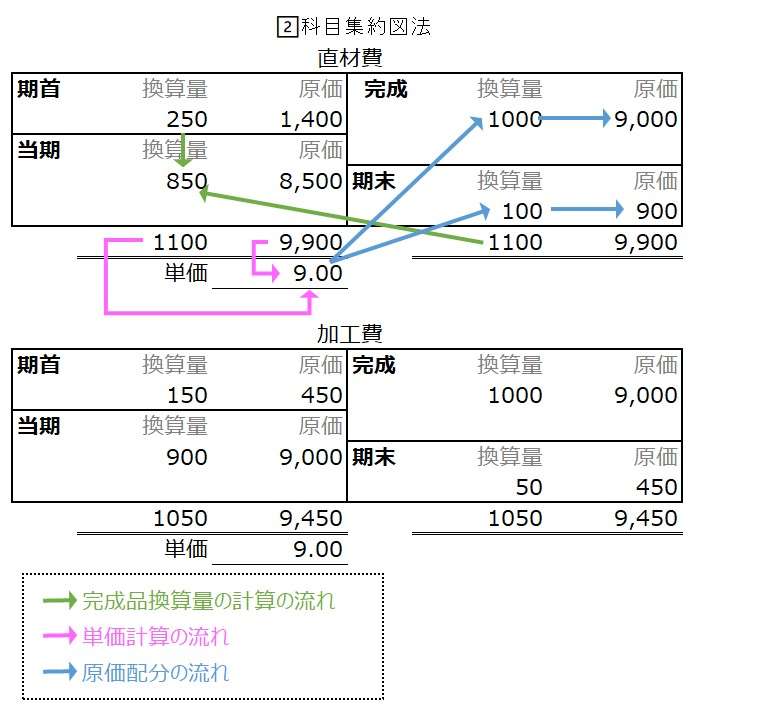
科目集約図法は、関連数値の近接性による分かりやすさ、完成品換算量の推計方法の取り違えが起きにくい、という2つの長所を取込んだものである。

人によれば、最もバランスのとれた図法と評価されるときもある。

灰色文字は、配置を決め打ちにしていれば、わざわざ書き込む必要はない。資格試験対策として事前練習を積み重ねていけば、やがていちいち書き込まなくても相対的位置で判別できるようになる（はず）。

原価集約図法

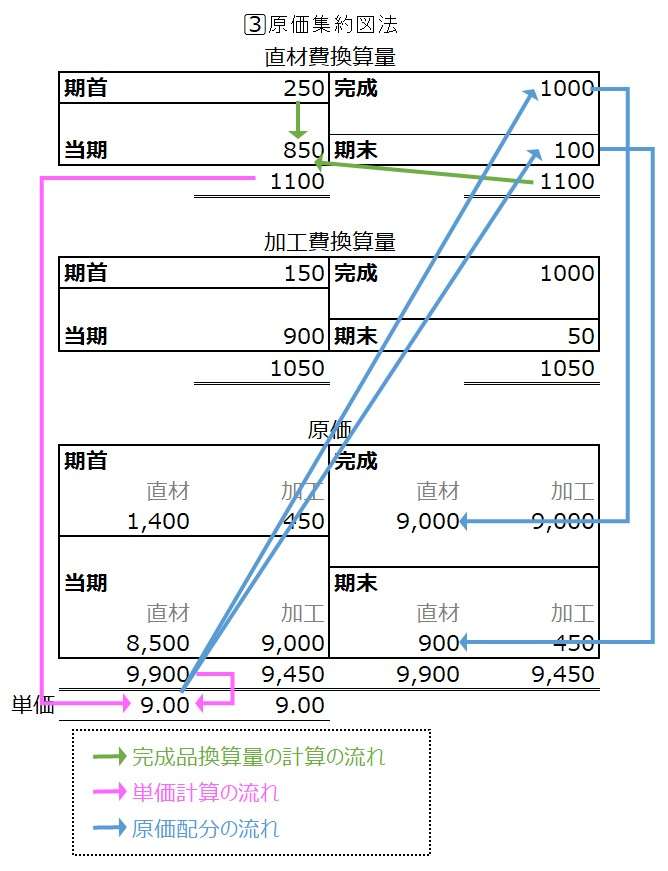
原価集約図法は、資格試験などで、仕損減損の処理や工程別計算など、複雑な完成品換算量の推計を必要としており、最終的に求められている答えが、完成品総合原価そのものである場合に用いられることが多い。

ただし、換算量ボックス２つにつき、原価ボックス1つであるため、計算途中で換算量の適用を間違える可能性があるので要注意だ。

灰色文字は、配置を決め打ちにしていれば、わざわざ書き込む必要はない。資格試験対策として事前練習を積み重ねていけば、やがていちいち書き込まなくても相対的位置で判別できるようになる（はず）。

換算量集約図法

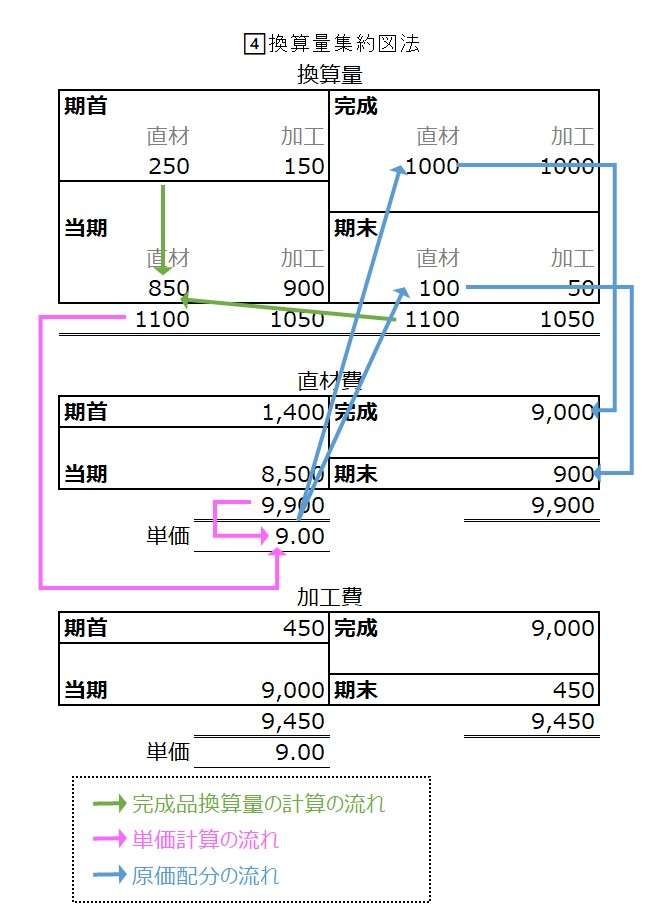
換算量集約図法は、資格試験などで、単純総合原価計算など比較的構造が複雑ではないケースで、直接材料費や加工費そのものを問われている場合に効率的な図法となる。

ただし、換算量ボックス１つにつき、原価ボックス２つであるため、計算途中で換算量の適用を間違える可能性があるので要注意だ。

灰色文字は、配置を決め打ちにしていれば、わざわざ書き込む必要はない。資格試験対策として事前練習を積み重ねていけば、やがていちいち書き込まなくても相対的位置で判別できるようになる（はず）。

個別図法

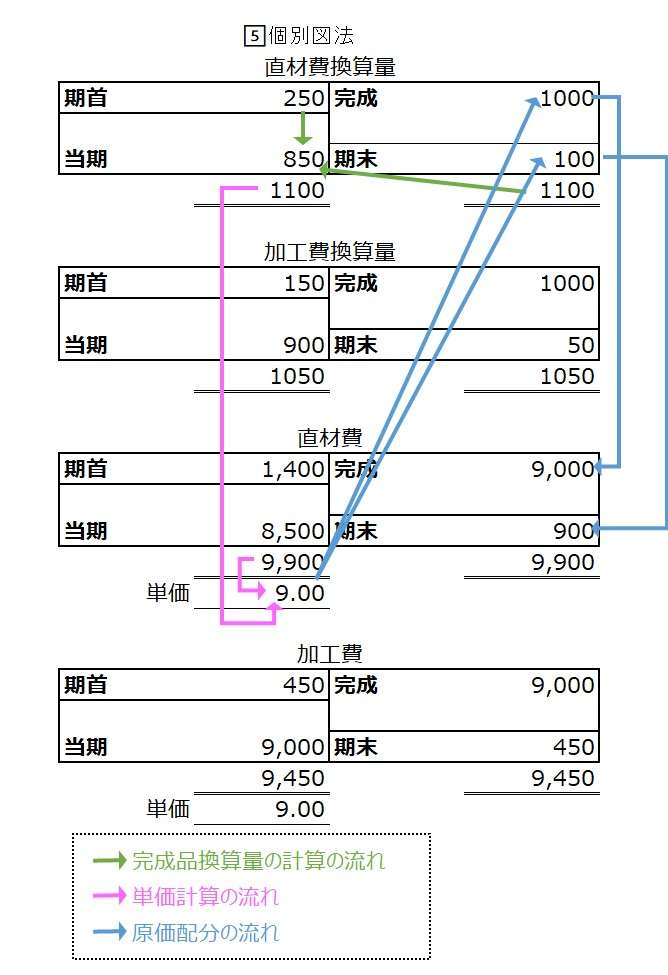
個別図法は、最もボックス数が多くなる図法で、ボックス間の関連性を追っかけるのが面倒くさいので忌避する人も多い図法である。

しかし、ひとつの目的ごとにボックスが独立している（混ぜるな危険！）ので、完成品換算量の推計、それぞれの原価配分を慎重に計算しなければならない初心者が手始めに書き慣れるために使用する目的には最適である。

なお、Excel等の表計算ソフトを使って、ワークシートを作成したり、ITシステムの概要設計資料とする場合には、この図法の方が他人との共通理解を得やすい（個人的経験談）。

●合計
\( \displaystyle \bf 完成品総合原価 = 完成品直接材料費 + 完成品加工費 = 9,000円 + 9,000円 = 18,000円 \)
\( \displaystyle \bf 期末仕掛品原価 = 期末仕掛品直接材料費 + 期末仕掛品加工費 = 900円 + 450円 = 1,350円 \)

●検算

期首仕掛品	直材費	1,400円	完成品	直材費	9,000円
1,850円	加工費	450円	18,000円	加工費	9,000円
当期製造費用	直材費	8,500円	期末仕掛品	直材費	900円
17,500円	加工費	9,000円	1,350円	加工費	450円
借方合計		19,350円	貸方合計		19,350円

[第1法]修正FIFO-簡便法

以下に続く先入先出法（FIFO）については、ボックス図法は「5⃣個別図法」による表記とする。

この[第１法]は、最速で先入先出法の問題を解くためということなら、ボックス図法と組み合わせると最強になる。下図のように、データフロー・処理フロー共に最もシンプルでかつ一本道だからとても分かりやすい。

●合計
\( \displaystyle \bf 完成品総合原価 = 完成品直接材料費 + 完成品加工費 = 8,900円 + 8,950円 = 17,850円 \)
\( \displaystyle \bf 期末仕掛品原価 = 期末仕掛品直接材料費 + 期末仕掛品加工費 = 1,000円 + 500円 = 1,500円 \)

●検算

期首仕掛品	直材費	1,400円	完成品	直材費	8,900円
1,850円	加工費	450円	17,850円	加工費	8,950円
当期製造費用	直材費	8,500円	期末仕掛品	直材費	1,000円
17,500円	加工費	9,000円	1,500円	加工費	500円
借方合計		19,350円	貸方合計		19,350円

[第2法]修正FIFO-原価計算基準 準拠法

[第２法]は、当期受入換算量を求めるのに、わざわざ、完成品量から期首仕掛品換算量を差し引いて当期加工当期完成分を計算してから、期末仕掛換算量と足しこむという計算手順が[第１法]より多い分だけ計算が遅くなる。

そして、残念なことに、一手間増やしたとしても、中途半端な情報（当期加工当期完成分原価）しか得られず、純粋先入先出法の結果にもならない。

さらに完成品原価を求めるには、この原価と期首仕掛品原価を合計してやる必要まで生じる。

●合計
\( \displaystyle \bf 完成品直材費 = 期首仕掛品直材費 + 当期加工当期完成分直材費 = 1,400円 + 7,500円 = 8,900円 \)
\( \displaystyle \bf 完成品加工費 = 期首仕掛品加工費 + 当期加工当期完成分加工費 = 450円 + 8,500円 = 8,950円 \)
\( \displaystyle \bf 完成品総合原価 = 完成品直接材料費 + 完成品加工費 = 8,900円 + 8,950円 = 17,850円 \)
\( \displaystyle \bf 期末仕掛品原価 = 期末仕掛品直接材料費 + 期末仕掛品加工費 = 1,000円 + 500円 = 1,500円 \)

●検算

期首仕掛品	直材費	1,400円	完成品	期首仕掛品分	直材費	1,400円
1,850円	加工費	450円	17,850円	1,850円	加工費	450円
				当期加工当期完成品分	直材費	7,500円
				16,000円	加工費	8,500円
当期製造費用	直材費	8,500円	期末仕掛品		直材費	1,000円
17,500円	加工費	9,000円	1,500円		加工費	500円
借方合計		19,350円	貸方合計			19,350円

[第3法]純粋FIFO-米国法

[第3法]は、純粋先入先出法として、完成品原価の内訳を厳格に、❶期首仕掛品原価、❷期首仕掛品当期加工分原価、❸当期着手当期完成品原価、の３つに分けることで、前期と当期の原価能率の違いを明確にする手法に忠実な計算方法である。

そもそも、原価配分計算の迅速化を目的に利用されるであろうボックス図法と、正確な完成品原価の内訳情報を得ようとする[第３法]の食べ合わせはよくない。

しかしながら、米国の各種会計資格試験対策では、この方法で指導されるから、それらを受験する場合には、この手法も知っておいた方がテキスト・問題集への取り組みが楽になるだろう。

（筆者はあくまで[第１法]で押し切ったが。。。）

●合計
\( \displaystyle \bf 完成品直材費 = 期首仕掛品直材費 + 期首仕掛品当期加工分直材費 + 当期着手当期完成分直材費 \)
\( \displaystyle \bf 完成品直材費 = 1,400円 + 0円 + 7,500円 = 8,900円 \)
\( \displaystyle \bf 完成品加工費 = 期首仕掛品加工費 + 期首仕掛品当期加工分加工費 + 当期着手当期完成分加工費 \)
\( \displaystyle \bf 完成品加工費 = 450円 + 1,000円 + 7,500円 = 8,950円 \)
\( \displaystyle \bf 完成品総合原価 = 完成品直接材料費 + 完成品加工費 = 8,900円 + 8,950円 = 17,850円 \)
\( \displaystyle \bf 期末仕掛品原価 = 期末仕掛品直接材料費 + 期末仕掛品加工費 = 1,000円 + 500円 = 1,500円 \)

●検算

期首仕掛品	直材費	1,400円	完成品	期首仕掛品分	直材費	1,400円
1,850円	加工費	450円	17,850円	1,850円	加工費	450円
				期首仕掛品当期加工分	直材費	0円
				1,000円	加工費	1,000円
				当期着手当期完成品	直材費	7,500円
				15,000円	加工費	7,500円
当期製造費用	直材費	8,500円	期末仕掛品		直材費	1,000円
17,500円	加工費	9,000円	1,500円		加工費	500円
借方合計		19,350円	貸方合計			19,350円

[第4法]修正FIFO-プロセス準拠法

[第4法]は、意図せずに純粋先入先出法となる方法で、計算ルートも一本道にならず、最も複雑な計算プロセスを要する。ものの流れ（生産プロセス）に最も忠実になろうとして人間側（計算方法側）が合わせに行く方法である。

それゆえ、計算の迅速化を目的とするボックス図法とは最も親和性が無い。

ボックス図内に登場する「期末仕掛品次期加工分」の数字にどうやって原価を配分するかで悩んで試験時間が終わりそうだ（正解は、当期発生の原価は一切振らない）。

[第１法][第３法]に比べて優れた点がみられないので、計算の最速化目的なら[第１法]、純粋先入先出法の実現目的なら[第３法]を選択しておけば事足りるだろう。

●合計
\( \displaystyle \bf 完成品直材費 = 期首仕掛品直材費 + 期首仕掛品当期加工分直材費 + 当期着手当期完成分直材費 \)
\( \displaystyle \bf 完成品直材費 = 1,400円 + 0円 + 7,500円 = 8,900円 \)
\( \displaystyle \bf 完成品加工費 = 期首仕掛品加工費 + 期首仕掛品当期加工分加工費 + 当期着手当期完成分加工費 \)
\( \displaystyle \bf 完成品加工費 = 450円 + 1,000円 + 7,500円 = 8,950円 \)
\( \displaystyle \bf 完成品総合原価 = 完成品直接材料費 + 完成品加工費 = 8,900円 + 8,950円 = 17,850円 \)
\( \displaystyle \bf 期末仕掛品原価 = 期末仕掛品直接材料費 + 期末仕掛品加工費 = 1,000円 + 500円 = 1,500円 \)

●検算

期首仕掛品	直材費	1,400円	完成品	期首仕掛品分	直材費	1,400円
1,850円	加工費	450円	17,850円	1,850円	加工費	450円
				期首仕掛品当期加工分	直材費	0円
				1,000円	加工費	1,000円
				当期着手当期完成品	直材費	7,500円
				15,000円	加工費	7,500円
当期製造費用	直材費	8,500円	期末仕掛品		直材費	1,000円
17,500円	加工費	9,000円	1,500円		加工費	500円
借方合計		19,350円	貸方合計			19,350円

原価管理 Cost Management 体系

1	原価測定のコンセプト	Measurement Concepts
2	原価集計システム	Cost Accumulation Systems
3	オーバーヘッドコスト	Overhead Costs
4	サプライチェーンマネジメント	SCM: Supply Chain Management
5	カイゼン	Business Process Impruvement

あわせて読みたい