原価計算基準 二二 等級別総合原価計算

原文
解説
ポイント
1. 設例
原価計算基準逐条詳解

原文

二二等級別総合原価計算

　等級別総合原価計算は、同一工程において、同種製品を連続生産するが、その製品を形状、大きさ、品位等によって等級に区別する場合に適用する。

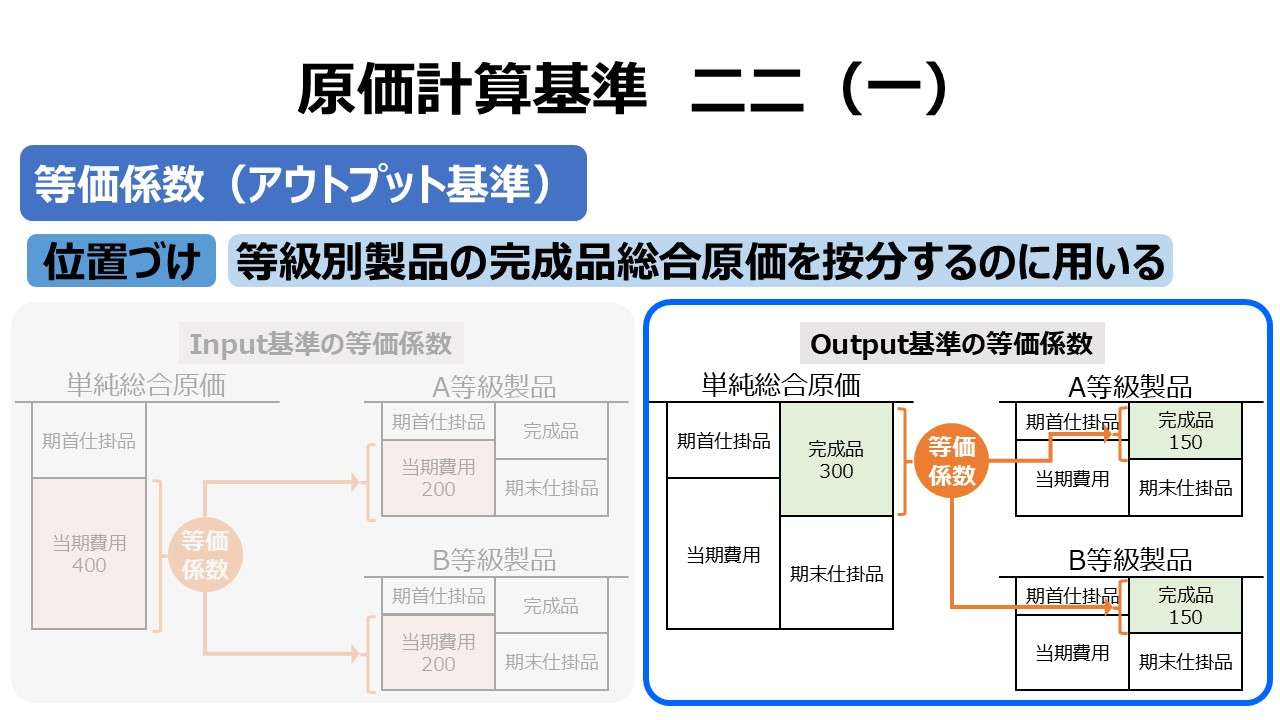
　等級別総合原価計算にあっては、各等級製品について適当な等価係数を定め、一期間における完成品の総合原価又は一期間の製造費用を等価係数に基づき各等級製品にあん分してその製品原価を計算する。

　等価係数の算定およびこれに基づく等級製品原価の計算は、次のいずれかの方法による。

（以下省略）
第二章　実際原価の計算｜原価計算基準

解説

等級別総合原価計算に関する規定の位置づけ

原価計算基準第二章第四節の製品別計算の各規定のツリー構造は下記の通り。

第四節原価の製品別計算
- 一九原価の製品別計算および原価単位
- 二〇製品別計算の形態
  - 二一単純総合原価計算
    - 二四総合原価計算における完成品総合原価と期末仕掛品原価
    - 二五工程別総合原価計算
      - 二六加工費工程別総合原価計算
    - 二七仕損および減損の処理
    - 二八副産物等の処理と評価
    - 二九連産品の計算
    - 三〇総合原価計算における直接原価計算
  - 二二等級別総合原価計算 ☚今ここ
  - 二三組別総合原価計算
  - 三一個別原価計算
    - 三二直接費の賦課
    - 三三間接費の配賦
    - 三四加工費の配賦
    - 三五仕損費の計算および処理
    - 三六作業くずの処理

総合原価計算に共通の話題は、基準二一で単純総合原価計算の紹介をした後、基準二四から基準三〇の間で触れられる。そこから派生的な総合原価計算として、等級別と組別が個別に解説される順番と考えるのが実質的な説明順だ。

これは逆に言うと、基準の項番通りに従い、形式的な順番に従うと、総合原価計算の内容説明に一切触れずに「基準二二」でいきなり派生形（応用編）の等級別総合原価計算についての言及が始まってしまうということだ。

本稿の初稿は、少なくとも総合原価計算の基礎である基準二四までの解説を終えた後に執筆されている。

基準二二等級別総合原価計算の規定内構造

さらに、基準二二総合原価計算の場合は、規定そのものが比較的長文でいくつかのブロックに分かれている。そしてこれが最終的にあかん・・・やつなのだが、実は、「基準二二」の読解について学会でも見解に一致を見ていない。

それなのに、既に実務で使われていたり、等級別総合原価計算としての計算問題が資格試験で出題されるのは原価計算界の七不思議のひとつ（後の６つは？）なのだが、ここでは逐条解説が目的なのであるから、見解が分かれていることを前提に、それぞれの学説の違いにまで踏み込んで解説していく。

その学説が分かれる理由の一つがそもそもの基準二二の規定の構造にも内在している。

[本文]
- 等級別総合原価計算の適用条件
- 等価係数の使用宣言
（一）output基準（製品の品質基準）による等価係数
（二）[前段]：input基準（原価財の消費量基準）による等価係数
（二）[後段]：総括的等価係数による簡便法

冒頭の[本文]部分で、等級別総合原価計算の適用条件と使用する等価係数に触れた後、等価係数の適用ケースを（一）（二）前段、後段の3つに分けて説明している。

しかしながら、等価係数の適用方法に関する説明に不備があり、いまだに定説がなく、議論百出のままなのである。その要因の一つが、（一）（二）前段・後段の条件分岐というか、ケース区分の基本的指針が不明確なことである。

本稿では、［本文］の解説にとどめておく。

等級別総合原価計算の適用条件

等級別総合原価計算は、同一工程において同種製品を連続生産する点は単純総合原価計算と同じである。ただし、対象製品が製品形状・大きさ・品位などによって等級に区分できるので、その等級別に総合原価計算を実施しようというものである。

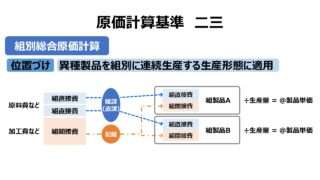
一般的に、等級別総合原価計算は、製品種別が全く異なる組別総合原価計算と、製品種別が一つに限定される単純総合原価計算の中間的形態に位置すると考えられる。

その位置づけに忠実に従うならば、それぞれの製品単位の計算について、組別製品ほど手間がかからない、等級別製品ならではの簡便法で計算処理がなされると考えるのが妥当だろう。

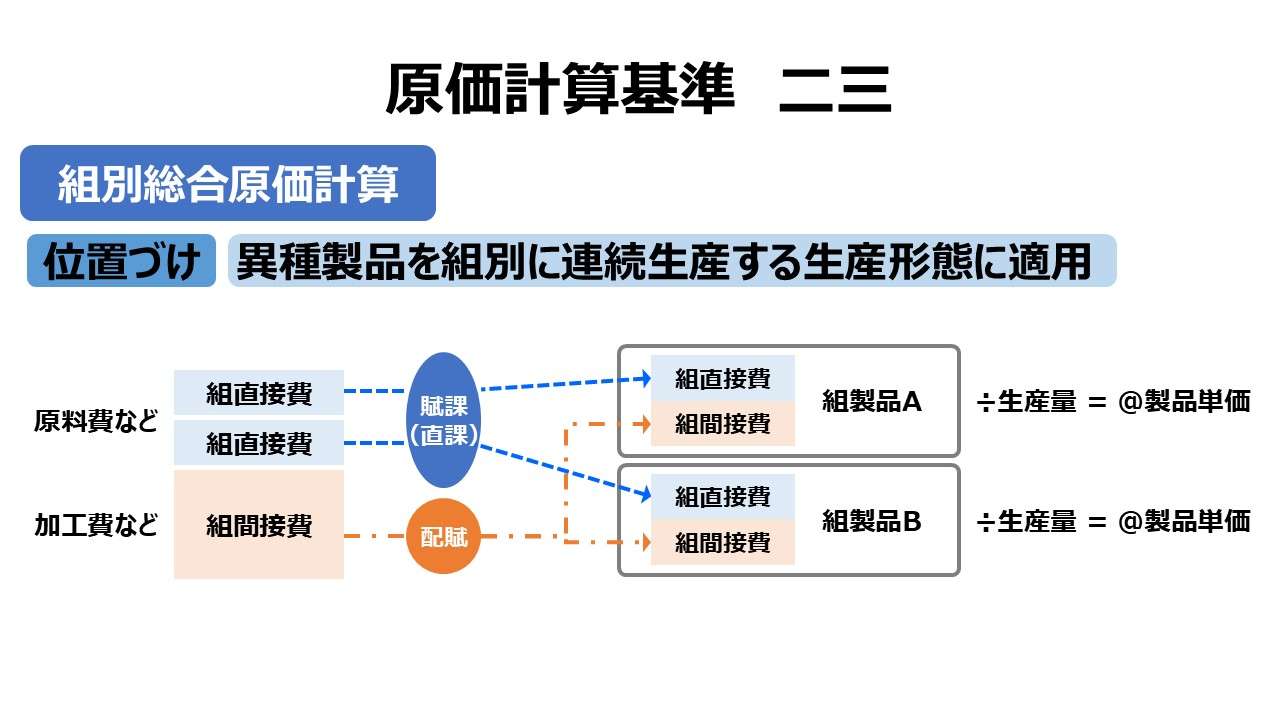
組別総合原価計算が「組間接費」を適当な配賦基準で各組別製品に配賦する代わりに、等級別総合原価計算では、等価係数を用いて「完成品総合原価」または「当期製造費用」をそれぞれの等級別製品に按分する。

下図は、組別総合原価計算の解説で用いた組間接費の配賦のされ方と等価係数の適用のされ方の対比図である。

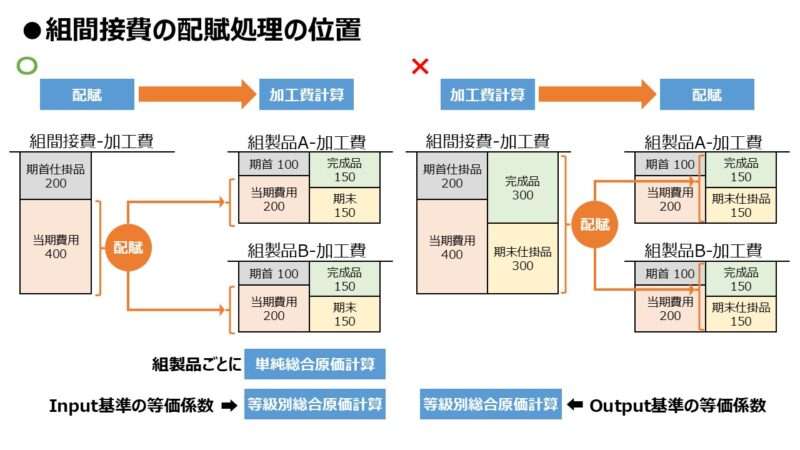
等価係数を用いて「当期費用」を按分する方式が、組別総合原価計算における組間接費の配賦に比すことができる。一方で、「完成品総合原価」に等価係数を適用して原価按分する方式が右に描かれている。

基準二二本文では、「一期間における完成品の総合原価又は一期間の製造費用を等価係数に基づき各等級製品にあん分」とあるが、上図では完成品原価と期末仕掛品を等価係数で按分しているように描かれている。

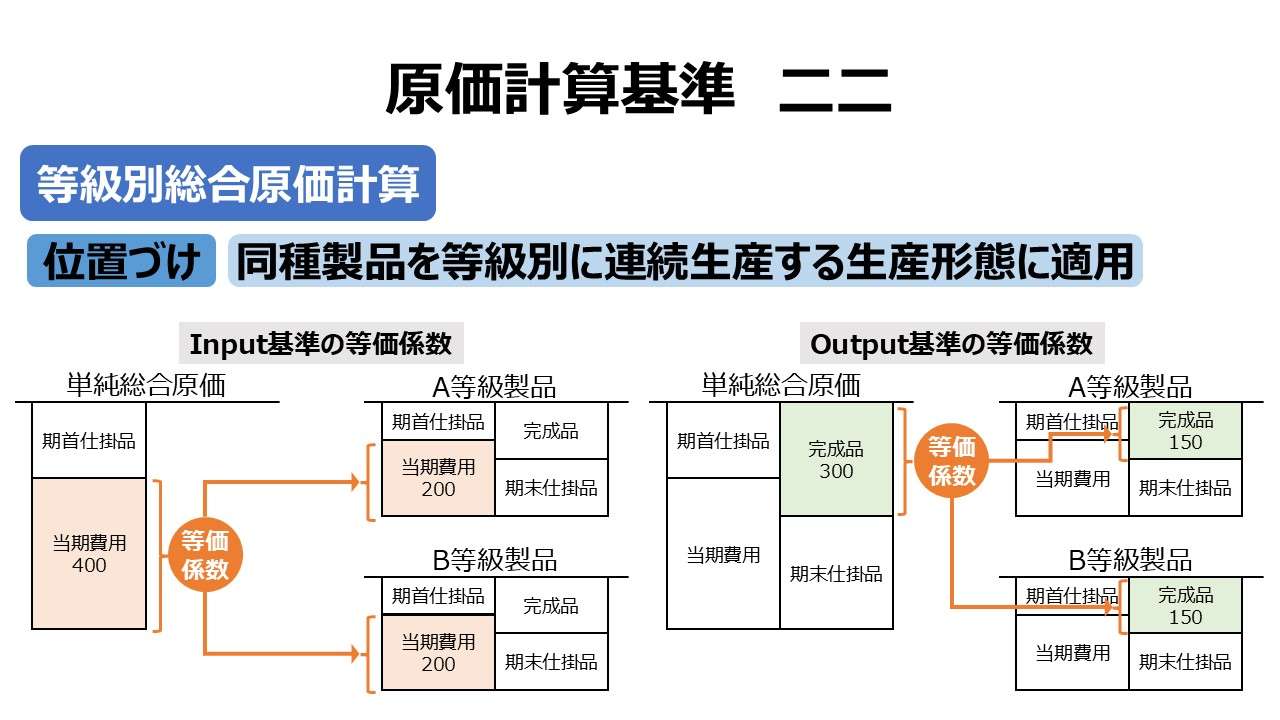
ちなみに、基準二二（一）では、output基準（製品の品質基準）による等価係数を使って「完成品原価」を等級別製品に按分し、基準二二（二）前段では、input基準（原価財の消費量基準）による等価係数を使って「当期製造費用」を等級別製品に按分する指示があることまでは分かっている。

まさしくこの点が「基準二二」が内包する規定不備の一端を垣間見ることができる部分でもある。つまり、基準二二本文の等価係数の適用説明部分では、期末仕掛品の処理が明言されていないのである（最初から対象外だから記載されていないとも解釈できるが、そうだと他にいろいろとまずいことが生じる。別稿にて解説予定）。

しかしながら、等級別総合原価計算が組別総合原価計算の簡便法の位置づけである、という基本姿勢の方を重視すれば、それぞれの等級別製品はあたかも一種類の製品として、一括して単純総合原価計算を用いて計算した後、等価係数を用いてそれぞれの等級別別製品へ原価按分するという考え方にも一定の支持があることは頷ける。

等価係数

製鋼工場で製造される各種規格の厚さの異なる鋼板、合板製造工場でラワン材を貼り合わせて製作された厚さの異なる各種合板、鋳物工場で製造される形状・重量が異なる各種鋳造品などは、いずれも同じ工場の同じ工程で連続的・反復的に生産される同種製品ともいえる。

例えば鋳物工場ならば、砂型に用いる砂は直接材料費として、それぞれの規格品ごとに投入量から識別できるから、組直接費に相当するだろう。各種砂型を用いて実際に鋳物を吹く作業は共通作業だから、ここの加工費は組間接費ということになるだろう。

つまり、正確を期すために、等級別製品とされるものに、組別総合原価計算を適用することは比較的容易であり、また、組別総合原価計算を適用した方が正確な原価計算ができる。

そこで敢えて等価係数を用いて等級別原価計算を試みる目的は、計算の手間を省略して簡便化したいという意図を達成するほかにない。

上記の等級別製品は、基本的に同種製品であり、製品相互間の差異は、ただ厚さや重量、口径といった規格が違うだけなのだから、製品相互間の製造原価発生額の差異は、何らかの物量的基準（製品単位当たりの重量・厚さ・長さ・面積・容量・純分度・熱量・硬度）や、投入する原料や労働力の消費量（作業時間）の差異と合理的に結びつけることが容易であると推測される。

あるいは、一定量を試作することで、規格ごとの各種製品の標準原材料費や標準加工費が把握でき、規格ごとの製造原価の差異とを合理的に関係付けることが可能になるかもしれない。

こうした規格違いの同種製品をまとめて単純総合原価計算で処理して、一原価計算期間の製造費用を各等級別製品へ等価係数を用いて按分した方が、それぞれを組別総合原価計算を仕立てて計算してやるより、合理的に手数を省略して計算することができる。

まとめ

等級別総合原価計算は、同一工程で同種製品である等級別製品を連続生産する場合に適用する
等級別製品とは、同種製品であって規格違いのものをいう
基本的な考え方として、各等級のものをまとめて単純総合原価計算を適用した後、等価係数によって各等級別製品へ完成品原価を按分する

原価計算基準二三組別総合原価計算

原文　組別総合原価計算は、異種製品を組別に連続生産する生産形態に適用する。　組別総合原価計算にあっては、一期間の製造費用を組直接費と組間接費又は原料費と加工費とに分け、個別原価計算に準じ、組直接費又は原料費は、各組の製品に賦課し、組間接費又...

ポイント

設例

期首仕掛品・期末仕掛品が存在せず、単に当期製造費用を等価係数で按分するとてもシンプルなケースを想定する。

[等価係数関連情報]
Y製品：1個あたり重量が100kg ⇒ Y製品の等価係数を1.0とすると、重量比を使い、
Z製品：1個当たり重量が150kg ⇒ Z製品の等価係数を1.5とおける

[生産情報]
Y製品の生産量10個
Z製品の生産量20個

[原価情報]
当期製造費用
　直接材料費：2,000円
　加　工　費：5,000円

●積数按分法

単純総合原価計算における数量按分方式の等級別総合原価計算版。単なる数量ではなく、数量に等価計算を掛け算したもの（積数せきすう）を用いる。

\( \displaystyle \bf Y製品の積数＝等価係数 \times Y製品生産量 = 1.0 \times 10個 = 10個 \)
\( \displaystyle \bf Z製品の積数＝等価係数 \times Z製品生産量 = 1.5 \times 20個 = 30個 \)

\( \displaystyle \bf Y製品直接材料費＝\frac{~~~~~2,000円~~~~~}{10個+30個} \times 10個 = 500円 \)
\( \displaystyle \bf Z製品直接材料費＝\frac{~~~~~2,000円~~~~~}{10個+30個} \times 30個 = 1,500円 \)

\( \displaystyle \bf Y製品加工費＝\frac{~~~~~5,000円~~~~~}{10個+30個} \times 10個 = 1,250円 \)
\( \displaystyle \bf Z製品加工費＝\frac{~~~~~5,000円~~~~~}{10個+30個} \times 30個 = 3,750円 \)

\( \displaystyle \bf Y製品完成品原価＝500円 + 1,250円 = 1,750円 \)
\( \displaystyle \bf Z製品完成品原価＝1,500円 + 3,750円 = 5,250円 \)

\( \displaystyle \bf Y製品直接材料費単価＝500円 \div 10個 = @50.0円/個 \)
\( \displaystyle \bf Z製品直接材料費単価＝1,500円 \div 20個 = @75.0円/個 \)

\( \displaystyle \bf Y製品加工費単価＝1,250円 \div 10個 = @125.0円/個 \)
\( \displaystyle \bf Z製品加工費単価＝3,750円 \div 20個 = @187.5円/個 \)

\( \displaystyle \bf Y製品単価＝ @50.0円/個 + @125.0円/個 = @175.0円/個 \)
\( \displaystyle \bf Z製品単価＝ @75.0円/個 + @187.5円/個 = @262.5円/個 \)

●等価比率法

積数同士の比率を等価比率と呼ぶ。積数÷積数合計による百分率を用いて計算する方式。

\( \displaystyle \bf Y製品等価比率＝\frac{~~~~~10個~~~~~}{10個+30個} = 25\% \)
\( \displaystyle \bf Z製品等価比率＝\frac{~~~~~30個~~~~~}{10個+30個} = 75\% \)

\( \displaystyle \bf Y製品直接材料費＝ 2,000円 \times 25\% = 500円 \)
\( \displaystyle \bf Z製品直接材料費＝ 2,000円 \times 75\% = 1,500円 \)

\( \displaystyle \bf Y製品加工費＝5,000円 \times 25\% = 1,250円 \)
\( \displaystyle \bf Z製品加工費＝5,000円 \times 75\% = 3,750円 \)

\( \displaystyle \bf Y製品完成品原価＝500円 + 1,250円 = 1,750円 \)
\( \displaystyle \bf Z製品完成品原価＝1,500円 + 3,750円 = 5,250円 \)

\( \displaystyle \bf Y製品直接材料費単価＝500円 \div 10個 = @50.0円/個 \)
\( \displaystyle \bf Z製品直接材料費単価＝1,500円 \div 20個 = @75.0円/個 \)

\( \displaystyle \bf Y製品加工費単価＝1,250円 \div 10個 = @125.0円/個 \)
\( \displaystyle \bf Z製品加工費単価＝3,750円 \div 20個 = @187.5円/個 \)

\( \displaystyle \bf Y製品単価＝ @50.0円/個 + @125.0円/個 = @175.0円/個 \)
\( \displaystyle \bf Z製品単価＝ @75.0円/個 + @187.5円/個 = @262.5円/個 \)

●共通単価法

積数合計値による平均単価を用いて計算する方式。もちろん、実数による製品単価とは異なるので、試験問題などで製品単価が求められた際は、改めて製品単価を実数を使って再計算してやる必要がある。

\( \displaystyle \bf 直接材料費共通単価＝\frac{~~~~~2,000円~~~~~}{10個+30個} = @50円/個 \)
\( \displaystyle \bf 加工費共通単価＝\frac{~~~~~5,000円~~~~~}{10個+30個} = @125円/個 \)

\( \displaystyle \bf Y製品直接材料費＝ @50円/個 \times 10個 = 500円 \)
\( \displaystyle \bf Z製品直接材料費＝ @50円/個 \times 30個 = 1,500円 \)

\( \displaystyle \bf Y製品加工費＝ @125円/個 \times 10個 = 1,250円 \)
\( \displaystyle \bf Z製品加工費＝ @125円/個 \times 30個 = 3,750円 \)

\( \displaystyle \bf Y製品完成品原価＝500円 + 1,250円 = 1,750円 \)
\( \displaystyle \bf Z製品完成品原価＝1,500円 + 3,750円 = 5,250円 \)

\( \displaystyle \bf Y製品直接材料費単価＝500円 \div 10個 = @50.0円/個 \)
\( \displaystyle \bf Z製品直接材料費単価＝1,500円 \div 20個 = @75.0円/個 \)

\( \displaystyle \bf Y製品加工費単価＝1,250円 \div 10個 = @125.0円/個 \)
\( \displaystyle \bf Z製品加工費単価＝3,750円 \div 20個 = @187.5円/個 \)

\( \displaystyle \bf Y製品単価＝ @50.0円/個 + @125.0円/個 = @175.0円/個 \)
\( \displaystyle \bf Z製品単価＝ @75.0円/個 + @187.5円/個 = @262.5円/個 \)

補足

この設例は、期首仕掛品・期末仕掛品が存在しないため、平均法・先入先出法・後入先出法の違いを意識する必要が無い。

この計算フローの動きは、基準二二（二）後段の簡便法に近い。