- ダウンロード元は当サイトと同じサーバ内です。
- 当サイトは、GDPR他のセキュリティ規則に則って運営されています。
- ダウンロードしたファイルは自由に改変して頂いて構いません。
- 本データの取り扱いは、原則としてMicrosoft サービス規約に準拠しています。
- 内容に関するご質問などは、こちらからお願いします。
計算式
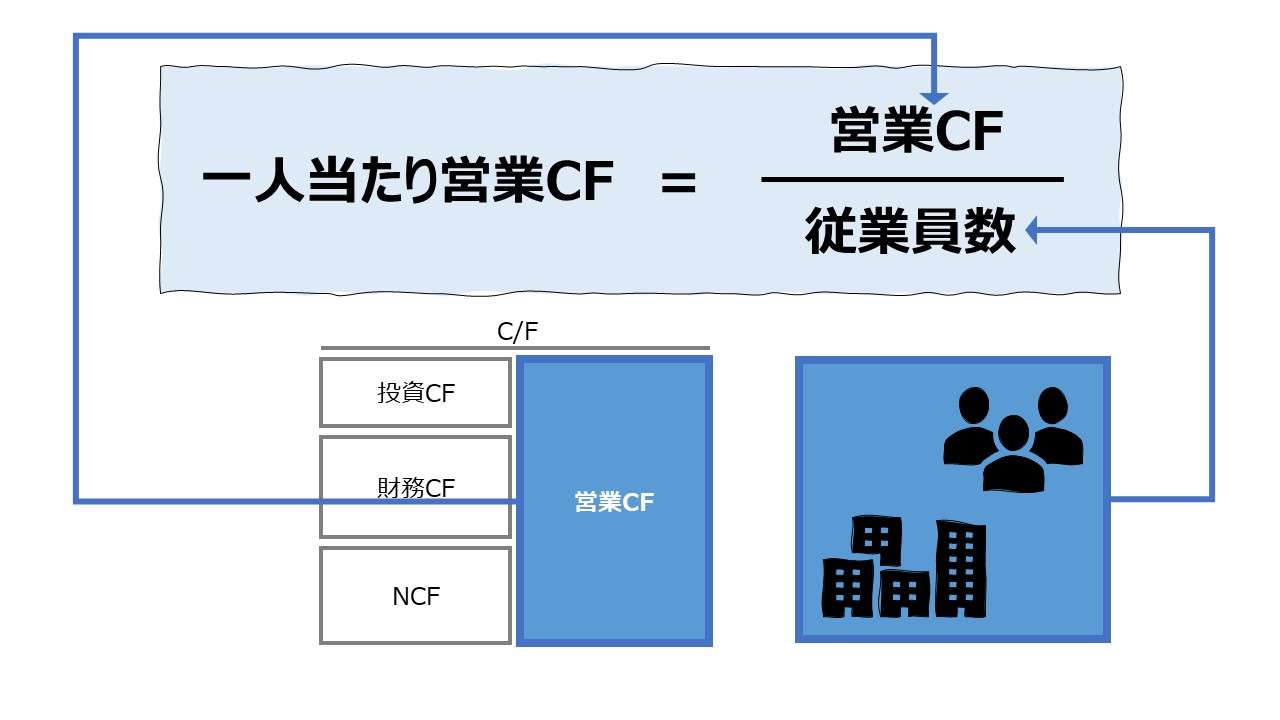
一人当たり営業CFは、事業に投下された労働力（人的資本）がどれくらいの営業CFを生み出したかという労働力単位当たりの効率を意味する。
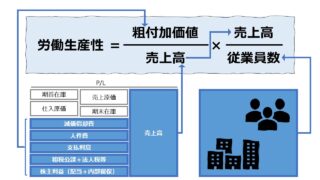
いわゆる労働生産性指標を構成する「一人当たり付加価値（Value Added per Employee）」のアウトプット基準を営業CFに置き換えたものである。
貸借対照表（B/S）上で、人的資本は資産計上されず、人件費がP/Lに費用として計上されるだけである。そこで、従業員という労働力の投入をヘッドカウント（人数）として量的把握し、投入された労働力当たりどれくらいの割合でアプトプットである営業CFを生み出すことができたのかを見る指標である。
通常は人数（ヘッドカウント、ウォームボディ）を用いるが、工数（稼働時間、就業時間）を用いることもある。なぜなら、パート・アルバイトとフル雇用の労働者の時間当たり生産性や時間当たり売上高等を同じ条件で算出することによって、正確に労働付加価値を計算するためである。
※生産活動に投入される労働資本量は、他に賃金総額や総労働時間を代替指標として用いることもできる。
ここでは、わかりやすさのため、単純に人数を用いる。
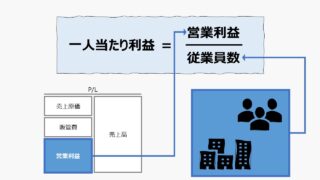
\( \displaystyle \bf 一人当たり営業CF＝ \frac{営業CF}{従業員数} \)
この指標の単位は「一人当たり」で、営業CFは法定通貨単位で表される金額指標であるから、ここでは通貨単位を「円」とすると、「円/人」と表現することができる。
分子はC/F項目で、会計的なP/L項目と同性質のフロー情報である。C/Fが1年未満の期間におけるものの場合は、年平均値に換算する必要がある。月次利益ならば12倍、単四半期利益ならば4倍する。
分母の従業員はB/S項目ではないが、資本と同様のストック概念で認識する。そのため、B/S項目と同様、平均在籍人数を用いる方法と、期首または期末の数字を用いる方法が存在する。平均在籍人数の方は、期首期末の平均値であり、（期首在籍人数＋期末在籍人数）÷２ で求める。
仮に、営業CFが単四半期の場合、従業員数も同じ単四半期の期首期末の値を用いて平均在籍人数を計算する必要がある。年平均残高は用いない。
また、従業員数の数え方には、次の2つの考え方がある。
①単純な頭数（Warm body）
②標準1日作業時間当たり人数（Full time equivalent）
①は、8時間労働者も4時間のパートタイマーも同じく一人二人と数えるやり方。②は、4時間のパートタイマーは0.5人分とカウントするやり方である。
よって、従業員の数え方は以下の4つの方法が存在することになる。
期首に、正社員（8時間勤務）5人、パートタイマー（4時間勤務）10人、期末に、正社員7人、パートタイマー8人だとしたら、下表のようになる。
| 期中在籍平均 | 期末在籍数 | |
|---|---|---|
| ヘッドカウント | 15人 | 15人 |
| 標準工数 | 10.5人 | 11人 |
例
営業CF 900万円
期中在籍平均人数 10人
\( \displaystyle \bf 一人当たり営業CF = \frac{900万円~~~}{10人} = 90万円/人 \)
- 営業CF：商品販売やサービス提供で得た収入から、仕入れや営業活動に必要な諸費用を差し引いた本来の営業活動から得られる営業活動から得られる現金収入
- 従業員数：経済活動に動員された人の数
定義と意味
一人当たり営業CFは、限られた人的投資の中で、最大のパフォーマンスを発揮して、可能な限り営業CFを稼ぎ出そうとする際の労働生産性の目標値として設定される指標のひとつである。
生産性分析の要諦は、❶インプットをできるだけ節約し（⇩）、❷アウトプットをできるだけ伸ばす（⇧）ものであるから、一人当たり営業CFについては、❶できるだけ投入人数を減らして、❷できるだけ営業CFを増やす、ことを目指した指標となる。
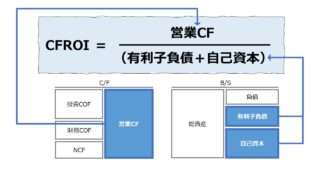
これは、資本生産性にも共通の構造であって、例えば、営業CFを用いた「キャッシュフロー投資利益率（CFROI: Cash Flow Return on Investment）」でも同様である。
そのことを分かりやすくするために、CFROIに「従業員数」を組み合わせてみると、
\( \displaystyle \bf CFROI=\frac{営業CF}{投下資本} = \frac{営業CF}{従業員数} \times \frac{従業員数}{投下資本} = 一人当たり営業CF \times \frac{1}{労働装備率（投下資本）} \)
※労働装備率=投下資本÷従業員数で、資本装備率とも呼ぶ。一人当たり投下資本を指す
となる。
CFROIは、投下資本当たりの営業CFの大きさを示すが、それは、一人当たり営業CFと従業員への投下資本の割当比率（労働装備率の逆数）にブレークダウンされることが分かった。
CFROIという資本効率を上げるためには、従業員ごとの生産性を上げるか、従業員の生産性を上げるための資本投下量をどのように節約するかのトレードオフの状態から最も企業にとって好ましい組み合わせを選択していく問題なのだということである。
いささか煩雑になってくるが、上式をもう少し分析項目を加えて詳細にブレークダウンしていくと、
\( \displaystyle \bf CFROI=\frac{営業CF}{投下資本} = \frac{営業CF}{従業員数} \times \frac{従業員数}{投下資本} = \left( \frac{営業CF}{売上高} \times \frac{売上高}{従業員数} \right) \times \frac{従業員数}{投下資本} \)
\( \displaystyle \bf CFROI = CFマージン \times 一人当たり売上高 \times 投下資本の従業員への割当比率 \)
または
\( \displaystyle \bf CFROI = CFマージン \times 一人当たり売上高 \times \frac{1}{労働装備率（投下資本）} \)
となる。
ここから、投下資本の資本効率を最善にしてCFROIのパフォーマンスを最良にするためには、例えば下表のような施策展開とKPIマネジメントが有用である。
| 項目 | 施策 | 具体例 |
|---|---|---|
| CFマージン | 売上高の単位当たりキャッシュ回収率を上げる | 債権回収期間を縮める コストダウンを図る |
| 一人当たり売上高 | 従業員一人当たりの販売額を伸ばす | ネット注文など省力化を図る クロスマーケティングを実施する |
| 労働装備率 （投下資本） | 従業員一人当たりの投下資本量を節約する | 業務効率化による人員削減 資本生産性の観点を盛り込む |
解釈と使用法
通常は、前章で触れたCFROIのツリー展開とKPIマネジメントに関するコメントはこの「解釈と使用法」の章の役割であった。
ここでは、生産性分析指標のツリー展開について理解が難しいと思われるポイントについてコメントしたい。
「生産性」の用語は、「収益性」の用語と混同されがちで、「収益性」とは煎じ詰めれば「収益率（利益率）」だというあまりに直線的な理解が世の中に先行していることもあり、「利益率」の式を無理やりツリー展開して、よくわからない解説が付されている記事を目にすることが多い。
例えば、前章でも取り上げた「CFマージン」を例にすると、
\( \displaystyle \bf CFマージン = \frac{営業CF}{売上高} = \frac{営業CF}{従業員数} \times \frac{従業員数}{売上高} \)
\( \displaystyle \bf CFマージン = 一人当たり営業CF \times 売上単位当たり所要従業員数 \)
となり、この式展開をKPIマネジメントに援用しようとすれば、
CFマージンを高めるためには、❶一人当たり営業CFを増やす、❷1円の売上を上げるために、できるだけ少ない従業員数でこなす、の2つが方策として想定されると理解するのが妥当だ。
❷の方は、1ドル＝105円から、1ドル＝120円になることを、「円安」と呼ぶのと同じくらい違和感があるだろう。
上記為替相場の「円安」とは、1円＝0.00952ドルから、1円＝0.00833ドルまで、円のドルへの交換価値が下がったから「円安」なのであって、ドルの方を固定して、105円→120円と目に見える形で円貨が増えているのにこれを「円が安くなった」と表現するのは感覚的に受け付けないのと同様の違和感である。
❷の方の理解促進のためには、次のような式展開の方が便利かもしれない。
\( \displaystyle \bf CFマージン = \frac{営業CF}{売上高} = \left( \frac{\frac{営業CF}{従業員数}}{\frac{売上高}{従業員数}} \right) = \frac{一人当たり営業CF}{一人当たり売上高} \)
CFマージンを上げるためには、一人当たり営業CFは増やす（⇧）必要があるが、同時に、一人当たり売上高は減らす（⇩）必要がある、というトレードオフの状態にある、という理解の方がスッと頭に入る。
もちろん、CFマージンを最初の目標にすることから生じるKPIマネジメント運用上の理解困難性であって、当初から、CFROI等の別の目標値を立てておけば、これほどの理解困難性が他の指標で発生することは少ない。
これは、本来は別観点である収益性分析における「利益率」に無理やり生産性分析における「労働生産性」や「資本生産性」の評価指標をこじ入れようとすることにより生じる不具合である。
本論は、学究肌の学者や理論の大家なら見落としがちの、キリキリと実務で揉まれた雑草魂を持つ実務家から指摘されるような類のTIPSではある。
蛇足ながら、次のような式の整理も知っておくと便利かもしれない。
\( \displaystyle \bf 投下資本回転率 = \frac{売上高}{投下資本} = \left( \frac{\frac{売上高}{従業員数}}{\frac{投下資本}{従業員数}} \right) = \frac{一人当たり売上高}{一人当たり投下資本} \)
\( \displaystyle \bf CFROI = \frac{営業CF}{投下資本} = \left( \frac{\frac{営業CF}{従業員数}}{\frac{投下資本}{従業員数}} \right) = \frac{一人当たり営業CF}{一人当たり投下資本} \)
したがって、利益率に労働生産性指標をそのまま入れ込むのではなく、例えば、CFROIを前提に考えれば、
程度の判断しかできないだろう。一人当たり営業CFなどの労働生産性は、投下資本などの資本生産性とペアで考えるべきで、一方を犠牲にしてもう一方の数値のみをよくするというのは、生産性分析の2大命題のうちのひとつである、「公平な付加価値の分配」に背反するものとなるからである。
シミュレーション
以下に、Excelテンプレートとして、FY17～FY22のトヨタ自動車の実績データをサンプルで表示している。
入力欄の青字になっている「期間」「営業CF」「短期有利子負債」「短期借入債務」「１年内返済長期借入債務」「長期有利子負債」「純資産」「従業員数」に任意の数字を入力すると、表とグラフを自由に操作することができる。
これらの値は、EDINETにて公開されている有価証券報告書から取得したものである。
どんな入力をしても、元ファイルが壊れることはない。入力し直したい、元に戻したい場合は、画面を更新（F5押下など）すれば、初期値に戻る。
自分の手元でじっくり検証したい場合は、上記のダウンロードボタンから、Excelをダウンロードすることをお勧めする。
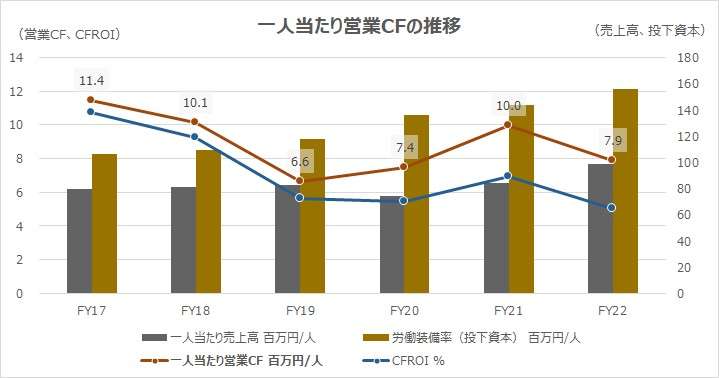
CFROIが波を打ちつつやや下降トレンドを示している。その変化は一人当たり営業CFの推移と同期をとった動きになっている。
関連する他指標も見てみると、一人当たり売上高はFY20を底に、FY22にかけて盛り上がっているし、一人当たり投下資本（労働装備率）に至っては、一本調子で上昇傾向を示している。
「キャッシュフロー投資利益率（CFROI: Cash Flow Return on Investment）」の事例分析でも触れたが、トヨタのこの期間のCFROIの低下傾向は偏に、運転資本の急激な水膨れがその主要原因である。
営業利益等の期間損益は上向きつつ、運転資本増が営業CFを下押ししている関係で、一人当たり営業CFもCFROIも低下傾向にある。
指標分析としては、一人当たり営業CFの改善方策に焦点を当てるべきだが、この事例に関しては、運転資本の水準が新型コロナ禍の影響を脱して正常化するのを待つしかないようだ。
参考サイト
同じテーマについて解説が付され、参考になるサイトをいくつか紹介しておく。
![[財務諸表分析]比率分析指標の体系と一覧](https://management-accounting.biz/wp-content/uploads/2020/07/financial-analysis-system.jpg)
[財務諸表分析]比率分析指標の体系と一覧
| 1 | 財務諸表分析の理論 | 経営分析との関係、EVAツリー |
| 2 | 成長性分析（Growth） | 売上高・利益・資産成長率、持続可能成長率 |
| 3 | 流動性分析（Liquidity） | 短期の支払能力、キャッシュフロー分析 |
| 4 | 健全性分析（Leverage） | 財務レバレッジの健全性、Solvency とも |
| 5 | 収益性分析（Profitability） | ROS、ROA、ROE、DOE、ROIC、RIなど |
| 6 | 効率性分析（Activity） | 各種資産・負債の回転率（回転日数）、CCC |
| 7 | 生産性分析（Productivity） | 付加価値分析、付加価値の分配 |
| 8 | 市場指標（Stock Market） | 株価関連分析、株主価値評価 |
コメント